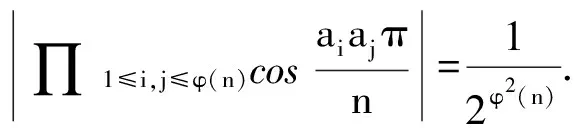数学问题解答
2019年2月号问题解答(解答由问题提供人给出)
(天津水运高级技工学校 黄兆麟 300456)
证明首先证明链中第一个不等式.
cosA+cosB+cosC
立得
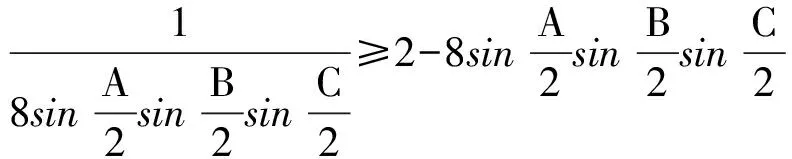
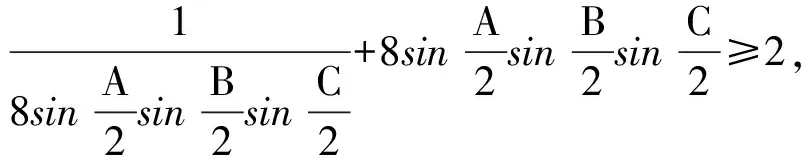
而以上最后一式由二元均值定理知显然成立,故链中第一个不等式成立.
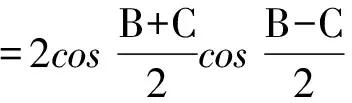
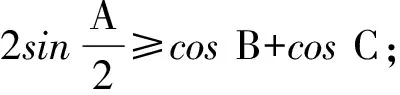
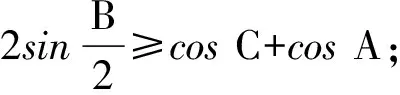
以上三式相加化简即得
≥cosA+cosB+cosC,
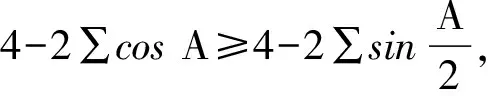
即链中第二个不等式成立.
而链中第三个不等式与熟知成立的
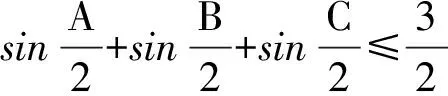
故知链中第三个不等式成立,至此命题获证.
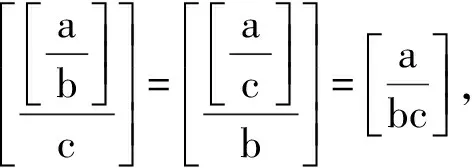
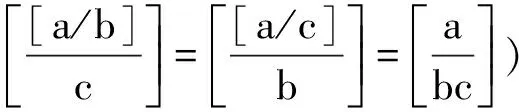
(贵州省织金县第六中学 邓波 552100)
证明现在考虑1,2,…,a中是bc的倍数的个数. 1,2,…,a中是bc的倍数的个数就是方程bct≤a的正整数t的解的个数.
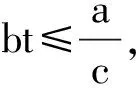

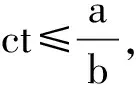

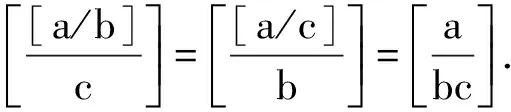
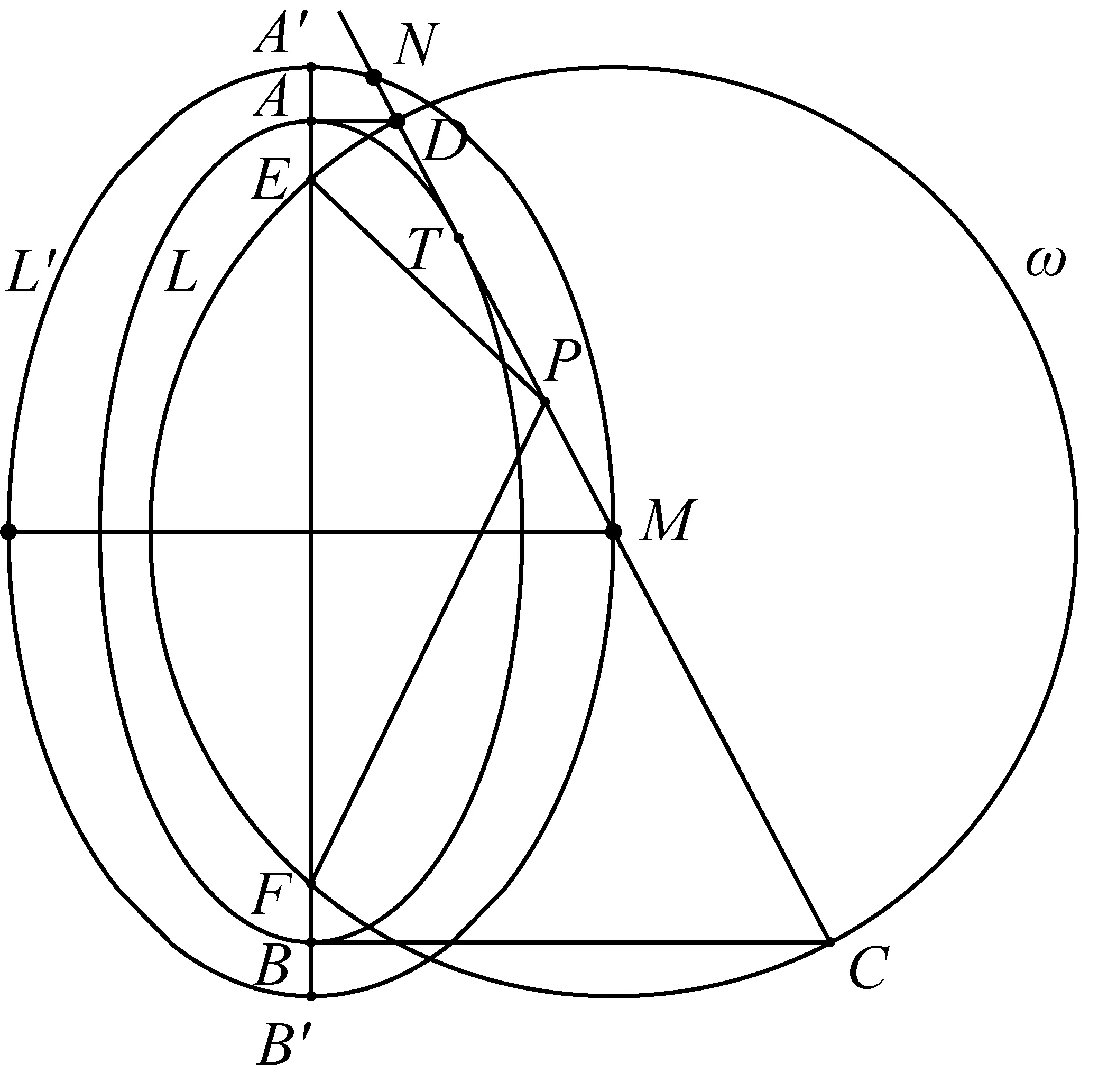
2468设不同的两点E,F在梯形ABCD的腰AB上, 且满足∠CED=∠CFD=∠ABC= 90°,在另一腰CD上求点P,使得AB≤PE+PF≤CD.

(河南辉县一中 贺基军 453600)
解在梯形ABCD中,不妨设AD 图1 如图1,由∠CED=∠CFD= 90° 知C,D,E,F四点共圆,CD为圆的直径. 设此圆为ω,圆心为M. 由∠ABC= 90° 知,AB的中垂线过点M,点E,F关于该中垂线对称. 作两个椭圆L和L′,它们具有公共焦点E,F,长轴分别为AB,A′B′,其中A′B′ =CD. 作DG⊥BC于点G,作点F关于CD的对称点F′. 因CD为圆ω的直径,故G,F′ 两点都在圆ω上. 连接EF′ 交CD于点T,连接FT,EG,DF′. 因矩形ABGD中EG=FD,又FD=F′D, 故EG=F′D, 因此圆内接四边形EGF′D为等腰梯形, 从而有EF′ =DG. 因TE+TF=TE+TF′ =EF′ =DG=AB, 图2 故由椭圆定义知,点T在椭圆L上, 于是点T为椭圆L与CD的公共点. 设∠ETF的平分线为t, 因F,F′ 两点关于CD对称, 故t∥FF′,即t⊥CD, 从而知CD为椭圆L在点T处的切线; 因点M为圆ω的圆心, 故ME+MF=2ME=CD=A′B′, 从而知M为椭圆L′ 的顶点. 根据AD 如果点N在线段MD上,即MN≤MD,则线段MN上任意一点为所求的点P(如图1). 这是因为,此时点P或在椭圆L上或在L外部,故有PE+PF≥AB;同时点P或在椭圆L′ 上或在L′ 内部,故有PE+PF≤CD,这里CD=A′B′. 如果点N在线段MD的延长线上,即MN>MD,则线段MD上任意一点为所求的点P(如图2). 这是因为,此时点D在椭圆L外部,同时点D在椭圆L′ 内部,故对于线段MD上任意一点P,都有AB≤PE+PF≤CD. 总之,在线段MN,MD中,较短线段上任意一点为所求的点P. 2469在△ABC中,设三边a,b,c上对应的高、角平分线、中线、旁切圆半径分别为ha,hb,hc;ta,tb,tc;ma,mb,mc;ra,rb,rc,∑表示循环和,求证: (1) (河南质量工程职业学院 李永利 467001) 证明设△ABC的面积、半周长、外接圆半径、内切圆半径分别为Δ,p,R,r,则 a+b+c=2p,ab+bc+ca=p2+4Rr+r2. 以下分五步证明(1)式成立. (2) (3) 而由恒等∑a=2p,∑ab=p2+4Rr+r2,Δ=pr, (4) 由(3)、(4)两式可知(2)式成立. (5) 可得 =∑a(b+c)2(p-b)(p-c) =∑[a(b2+c2)+2abc][p2-(b+c)p+bc] =∑a(b2+c2)[p2-(b+c)p+bc]+2abc∑[p2-(b+c)p+bc] =p2∑a(b2+c2)-p∑a(b2+c2)(b+c)+abc∑(b2+c2)+2abc(3p2-2p∑a+∑bc) =p2∑a(b2+c2)-p∑[a(b3+c3)+abc(b+c)]+2abc∑a2+2abc(-p2+∑bc) =p2∑a(b2+c2)-p∑a(b3+c3)-4p2abc+2abc∑a2+2abc(-p2+∑bc) =p2∑a(b2+c2)-p∑a(b3+c3)+abc[-6p2+∑a2+(∑a2+2∑bc)] =p2∑a(b2+c2)-p∑a(b3+c3)+abc(-2p2+∑a2), 又因 ∑a(b2+c2)=2p∑a2-∑a3, ∑a(b3+c3)=2p∑a3-∑a4, 且 ∑a2=2(p2-4Rr-r2), ∑a3=2p(p2-6Rr-3r2), ∑a4=2(p2-4Rr-r2)2-8p2r2, abc=4Rrp, 所以 =p2(2p∑a2-∑a3)-p(2p∑a3-∑a4)+abc(-2p2+∑a2) =2p3∑a2-3p2∑a3+p∑a4+abc(-2p2+∑a2) =2p3(2p2-8Rr-2r2)-6p3(p2-6Rr-3r2)+p[2(p2-4Rr-r2)2-8p2r2]+4Rrp[-2p2+2(p2-4Rr-r2)] =pr[p2(4R+2r)+2r2(4R+r)], (6) 于是,由(4)、(6)两式可知, (5)式等价于 ⟺8Rr(4R+r)≤p2(2R+r)+r2(4R+r) ⟺p2(2R+r)≥32R2r+4Rr2-r3. 由Gerretsen不等式p2≥16Rr-5r2可知, 欲证上式成立,只需证明 (16Rr-5r2)(2R+r)≥32R2r+4Rr2-r3 ⟺(16R-5r)(2R+r)≥32R2+4Rr-r2 ⟺32R2+6Rr-5r2≥32R2+4Rr-r2 ⟺2Rr-4r2≥0 ⟺2r(R-2r)≥0, 而由欧拉不等式R≥2r可知,上式显然成立,故(5)式成立. (7) ∑ab=p2=4Rr+r2, (8) 由(6)、(8)两式可知,(7)式等价于 ⟺p2(2R+r)+r2(4R+r) ≤2Rp2+8R2r+2Rr2 ⟺p2r≤8R2r-2Rr2-r3 ⟺p2≤8R2-2Rr-r2. 而由Gerretsen不等式p2≤4R2+4Rr+3r2可知, 欲证上式成立,只需证明 4R2+4Rr+3r2≤8R2-2Rr-r2 ⟺2R2-3Rr-2r2≥0 ⟺(R-2r)(2R+r)≥0, 而由欧拉不等式R≥2r可知上式显然成立,故(7)式成立. (9) 由熟知的不等式x2+y2+z2≥xy+yz+zx可知(9)式显然成立. (10) (11) (12) 于是由(11)、(12)两式可知,(10)式等价于 ⟺p2-4Rr-r2≤2p2-16Rr-4r2 ⟺p2≥12Rr+3r2, 由Gerretsen不等式p2≥16Rr-5r2可知,欲证上式成立,只需证明 16Rr-5r2≥12Rr+3r2 ⟺4Rr-8r2≥0 ⟺4r(R-2r)≥0, 而由欧拉不等式R≥2r可知,上式显然成立,故(10)式成立. 由以上五步证明的(2)、(5)、(7)、(9)、(10)五式可知(1)式成立. (安徽省岳西县汤池中学 杨续亮 246620) 解先证明一个等式 sin 66°-sin 30°=sin 18°+sin 6°. sin 66°-sin 6°-sin 18° =2cos 36°sin 18°-sin 18° =sin 54°-sin 18°=2cos36°sin18° 即sin 66°-sin 30°=sin 18°+sin 6°, 所以 sin 66°-sin 30°=sin 18°+sin 6° ⟺2cos 48°sin 18°=2cos 6°sin 12° ⟺cos 48°cos 72°=cos 6°cos 78° 2019年3月号问题 2471设n是一个大于1的奇数,数a1,a2,…,aφ(n)是1,2,…,n中与n互素的所有正整数. (浙江省富阳二中 许康华 311400) 2472设△ABC的三边长、相应的旁切圆半径、外接圆半径、内切圆半径、半周长和面积分别为a、b、c、ra、rb、rc、R、r、p和Δ, 则有 等号当且仅当△ABC为正三角形时成立. (安徽省太和县第二小学 任迪慧 236630) (山东省泰安市宁阳第一中学 刘才华 271400) 2474已知a,b,c>0,且abc=1,求证: (广东省广州市广东广雅中学 杨志明 510160) (江西师范高等专科学校 王建荣 335000)
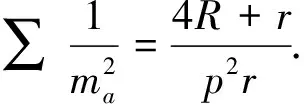
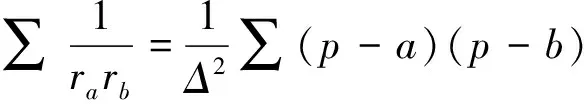
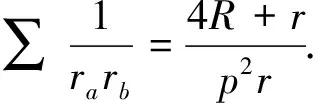
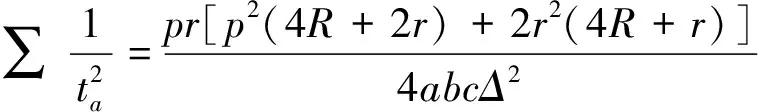
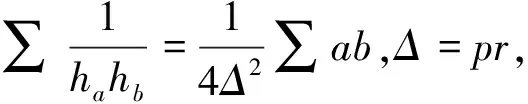
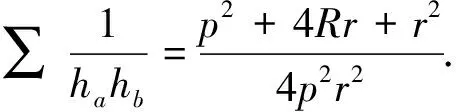
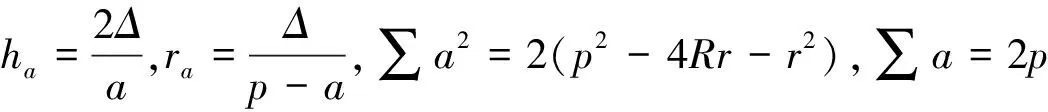
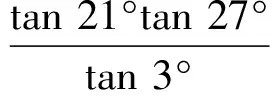
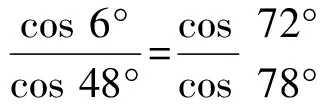
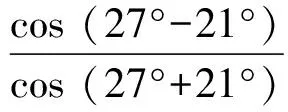
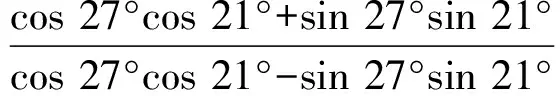
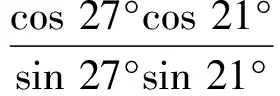
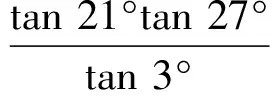
(来稿请注明出处——编者)