落实“五重五通”打造灵动课堂
——解析几何一轮复习中难点教学的实践与思考
张启兆
(无锡市青山高级中学 214000)
高三数学一轮复习是整个高考数学复习的基础,一轮复习以教材的知识体系作为复习的主要线索,帮助学生对学过的基础知识进行全面的梳理,并对基本技能、基本思想和基本活动经验进行总结、归纳,从而初步构建高中数学的网络.解析几何是历年高考必考的知识点之一.然而学生在解析几何学习中存在一系列难点:一是对解析几何中的基本概念与基本公式理解不深刻;二是对平面解析几何的基本思想理解不到位;三是代数运算能力弱.如何帮助学生有效地突破上述难点,是我们在解析几何的一轮复习中需要着力解决的问题.下面结合笔者的教学实践,谈一些认识和体会,供大家参考.
1 重问题,通本质,激活知识梳理
一轮复习不是对已学知识的简单重复和强化,而是一个再学习、提高综合运用能力的过程.对于高三复习课,如何梳理基础知识是高三数学老师必须解决的第一个问题,我们的做法是:实行问题导思,激活知识梳理,促进学生主动建构知识网络.课前,首先,教师要合理设计问题,然后提供知识复习整理提纲(学案),学生课前阅读课本,这样可以提高学生对课本知识和概念的参与度,避免课堂教学中因复习知识而占用大量的时间.接着,学生将课本中知识点整理到学案上进行理解和记忆,教师课前检查,目的是强化学生对基础知识和概念的记忆,为后面的学习提供集中、全面的基础知识复习材料.最后,教师将教学目的分解,以知识为线索编制4-5个题目,直接体现本节课知识点的应用,学生独立完成,要求题后总结所用知识点或方法,教师检查,目的是不断激发学生的学习动机,促进学生对基础知识和概念的应用.
案例1“抛物线”的教学片段.
课前笔者根据苏教版2012年第三版第52页内容提出了下面的问题:
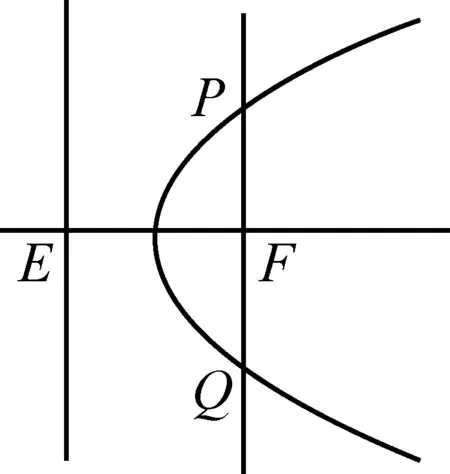
图1
设抛物线的轴和它的准线交于点E,过焦点垂直于轴的直线交抛物线于P、Q两点,如图1所示.求证:EP⊥EQ.
经过短暂的思考,笔者与学生进行了以下交流:
教师:大家准备从哪个角度来解决问题,是几何角度(即几何综合证明)还是代数角度(即通过计算来证明)?
学生:我准备从代数角度,通过计算两直线的斜率之积为-1.
教师:从代数角度是合适的,因为解析几何的基本思想是用代数方法来研究几何问题.从代数角度首先要做什么工作?
学生:建立平面直角坐标系.
教师:你准备怎样建?

图2
学生:以抛物线的轴为x轴,以线段EF的中点为坐标原点建系,如图2.
教师:抛物线的方程是什么?对应的焦点坐标和准线方程呢?

教师:你设的方程中p有什么几何意义?
美国著名数学教育家波利亚曾说:“一个专心且认真备课的老师能够拿出一个有意义的但不复杂的题目,去帮助学生挖掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域.”以问题为载体梳理知识框架的好处在于既能达成系统梳理知识、把握知识本质的目标,又能以问题为中心吸引学生积极参与其中,调动学生思维的积极性,改变课堂上被动接受的状态.
2 重基础,通概念,促进数学理解
解析几何的核心观点就是恰当运用代数的方法解决几何问题,基本思想是数形结合思想,核心方法是坐标法.数形结合思想和坐标法是统领全局的,解析几何就是在坐标系的基础上,用代数的方法研究几何问题的一门学科.
用解析法研究几何图形的性质,须先将几何图形置于坐标系下,让“形”与“数”对应起来,将“形”进行翻译转化:把点转化为坐标、把曲线转化为方程,把题目中明显的或隐含的解题所需要的一切几何特征,用数式和数量关系表示出来.
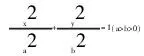
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点D(0,4)的直线l与椭圆C交于两点E、F;

(ⅱ)A是椭圆的右顶点,且∠EAF的角平分线是x轴,求直线l的斜率;
(ⅲ)以线段OE、OF为邻边作平行四边形OEFP,其中顶点P在椭圆C上,O为坐标原点.求O到直线l距离的最小值;
(ⅳ)若以EF为直径的圆过原点,求直线l的斜率;
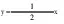
根据以上问题的求解过程,填写表1:
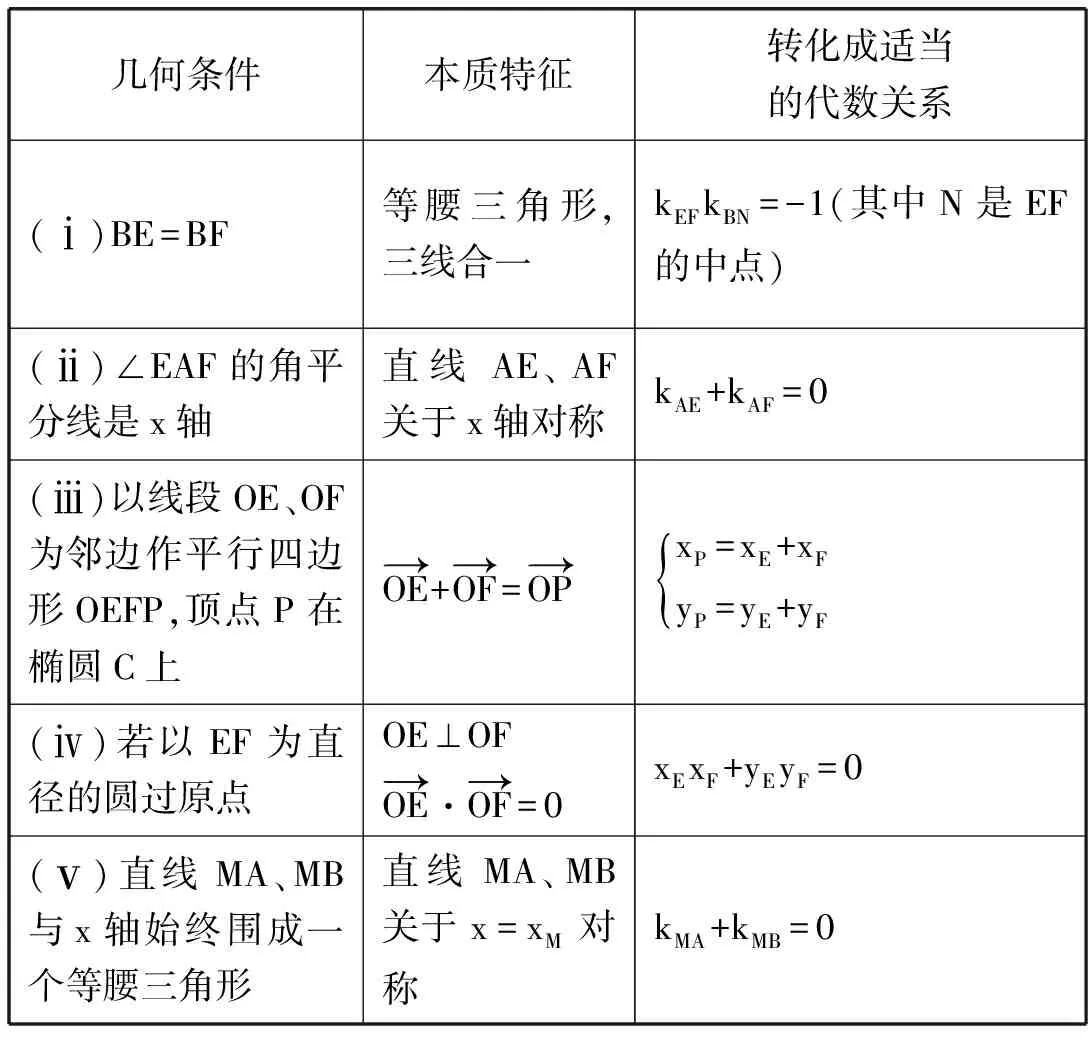
表1
通过这道例题,在不同问题情境中概括总结“几何条件转化成代数关系”的核心方法:分析几何条件的本质特征,选择适当的代数形式来表示.这种意识再提高就是“从现象到本质,抓住事物的本质认识事物”.常见的几何关系与几何特征的代数化有:①线段的中点:坐标公式;②线段的长:弦长公式;③三角形面积: 底×高,正弦定理面积公式;④夹角:向量夹角;两角差正切;余弦定理;正弦定理面积公式;⑤面积之比,线段之比:面积比转化为线段比,线段比转化为坐标差之比;⑥三点共线:利用向量或相似转化为坐标差之比;⑦垂直平分:两直线垂直的条件及中点坐标公式;⑧点关于直线的对称,点关于点,直线关于直线对称;⑨直线与圆的位置关系;⑩等腰三角形,平行四边形,菱形,矩形,正方形,圆等图形的特征.
要防止一种误区:基础题不讲,追求难题,背概念或公式,不提知识如何生成.教师应重视常规基础题的练习,从不起眼的解题细节抓起,利用“三种意识”:几何条件代数化、代数运算几何化、一般问题特殊化,打通解析几何的思路,夯实学生的基本知识和基本技能,提高学生的理解能力,才能解决更难的问题.
3 重过程,通思维,引领理性思考
面对问题,学生会经历审题、思考、解决、出现错误、修改、调整方案等一系列过程,在每个环节都会出现疑惑、纠结,而经过思考、实践产生的纠结也恰恰是解题能力提高的一个增长点.教学中我们要重视过程,做到:①要合理展示教师的思维过程.学生的思维往往是在模仿教师的思维中逐渐形成的,所以教师在课堂教学时应注意思维形式的“显化”.教师要尽量设法使学生看到,面对一个新问题,自己是怎样寻求解决思路的?其依据是什么?特别是在思路受阻后是如何调整思路的?为什么这样调整?等.千万不要给学生造成这样的错觉:老师很神,无论问题多难都能迎刃而解.要让学生在“跟随教师的思维过程”中学会思维,让数学变得自然.②要充分展示学生的思维过程.课堂教学中应给学生充分暴露和展示思维过程的机会,传统教学中的口头提问、板演等都是展示学生思维的方式.只有这样我们才能及时地发现学生的思维“闪光点”和存在的问题,并肯定正确、矫正错误,才能让学生在“过程”中有效地习得方法、达成技能、发展思维、建立思想、形成能力.
案例3试卷讲评片段.
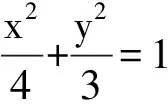
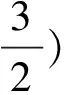
(2)设B(x1,y1),C(x2,y2),且3y1+y2=0,求当△OBC面积最大时,直线l的方程 .
教师:这道题你是怎样思考的?先分析第(1)小题.

图3
学生:由于本题没有给图,所以在读题时应该在草稿纸上先画个图(如图3),再从目标出发:要求△OBC面积的最大值,可以建立目标函数,设直线BC的方程为y=kx+b,把直线与椭圆方程联立,求出弦BC的长,再求出点O到直线BC的距离,我忘记讨论直线BC的斜率是否存在,被扣分了.
教师:这位同学的解题思路是常规方法,值得表扬. 如何表示△OBC面积是求解本题的关键,那么△OBC的面积还有其他表示方法吗?
学生:由于△OBC中,OB定长,故以OB为底边 ,问题转化为求点C到直线OB的距离的最大值.
教师:结合图形和已知条件,选择合适的解题路径,可以简化解析几何的运算 .
教师:下面我们请你谈谈对第(2)小题思考过程.
学生:我是仿照第(1)小题,设直线BC的方程为y=kx+b,把直线与椭圆方程联立,求出弦BC的长,……,然后做不下去了.
教师:那么△OBC的面积还有其他表示方法吗?
学生:由题意知,直线l与y轴不垂直,所以设直线l的方程为x=my+n,设直线l与x轴交于点A,把△OBC分割成便于表示底边与高的两个三角形求面积:
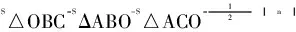
教师:这个思路值得大家借鉴,接下来请你尝试做一下.
……
教师:下面请哪位同学和大家分享一下解题过程.
……
4 重训练,通算理,培养运算能力
如何提高学生的运算能力?我们在课堂教学中做到以下四个方面:①要让学生准确理解和掌握基础知识、公式和法则;②注重学生基本运算技能的培养,课堂上要留出一定时间让学生进行当堂训练;③注重数学思想方法与运算技能的有机结合.运算能力发展到一定的水平,即形成了运算的基本方法和技能,此时还需不断运用有关的数学思想方法,如运算中的转化意识,将要计算的问题转化为容易求解的问题,这也是运算能力的一个重要组成部分;④重视算理算法,加强限时计算.注重积累,优化解题方法.教学中需要对学生的解题方法进行梳理、改造,让学生明白每一种方法的优点(适用面)和缺点(不适用面),从而在解题时根据具体情况,选择有效、便捷的方法解决问题.
比如,要两手抓. 一手抓基础:基本概念、基本方法、常见问题,“弦长公式”,“图形面积的计算”,“轨迹方程”,“定点定值——先猜后证”,“最值问题——目标函数”,“存在性问题——从特殊出发”, 运算基本功.一手抓思考:知其然更需知其所以然,带着思考去解题而不是带着套路去解题;帮助学生掌握处理解析几何问题的一般思维方法;给学生以“锻炼”思维的机会.
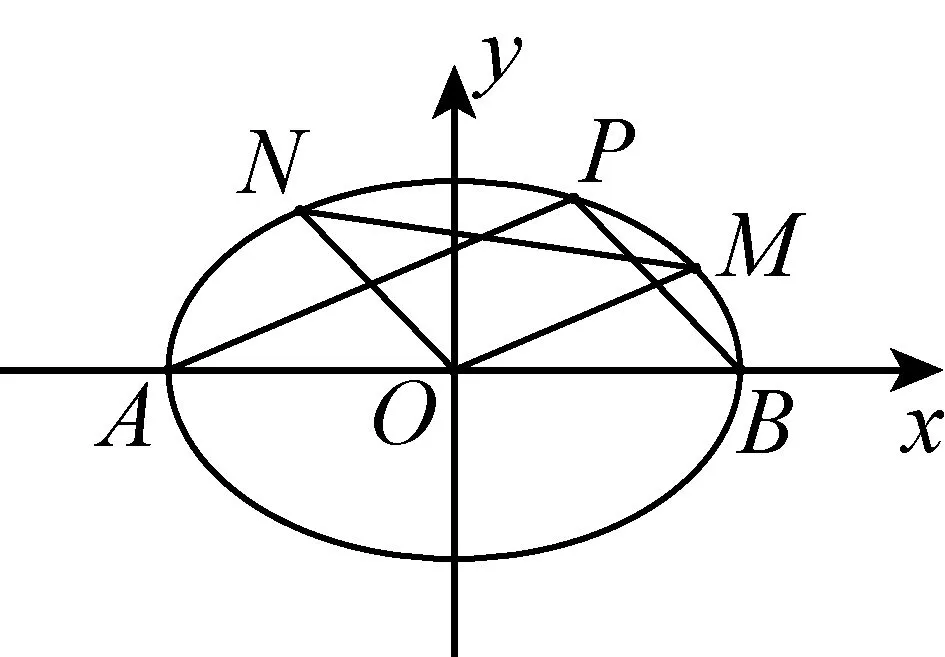
图4
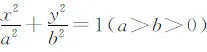
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点A作AP∥OM交椭圆C于点P,
求证:BP∥ON.
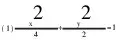
(2)教师:谈谈你对第(2)小题的理解,问题出在哪里?
学生:题目问题为求证:BP∥ON,但是我找不到所需证明的等价代数条件,因此无从下手.
教师:对于本题而言,需求证结论看起来确实突兀,我们来挖掘题目已有信息.
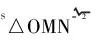
教师:题目中的条件AP∥OM意味着什么?
学生:意味着kAP=kOM.
教师:很好!因此,要验证kBP=kON,除了直接计算外,还可以如何进行验算?学生有所悟,但不是十分明确,教师进行第二次引导.
对圆而言,在圆周上找一点P与两点A,B连线斜率乘积为定值-1,即kAP·kBP=-1.对椭圆而言,是否有相似结论?
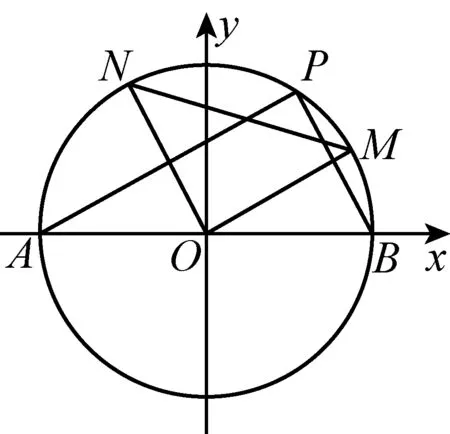
图5
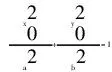
教师:对本题而言意味着什么?
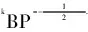
教师:很好!对于本题而言,我们接下来只需验证什么条件?
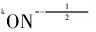
教师:我们研究解析几何问题可分为三步:生点、定点、译点.大家如何进行这三步?

教师:很好!还有其它思路吗?

教师:很好!下面请1、2小组按思路1计算,3、4小组按思路2计算.
5 重小结,通思想,提升数学素养
行为派心理学认为,初步形成的行为必须适时强化,不强化就会消退.高三复习通过课堂小结和单元小结对知识概括提炼,有利于学生建立良好的认知图式,强化知识,促进迁移.通过知识间的联系把知识进行整合,将难于理解的知识规律化,使学生零散的知识穿成串,结成网,变成“集成电路”印在学生的脑海里.此外,要重视解题过程中思想方法的提炼与运用,如①坐标法;②方程思想;③函数思想;④分类讨论;⑤数形结合;⑥对称思想;⑦参数思想.
案例5解析几何中变量的取值范围问题
问题1点P是抛物线C:y2=2x上的动点,点R,N在y轴上,圆(x-1)2+y2=1内切于△PRN,求△PRN的面积的最小值.
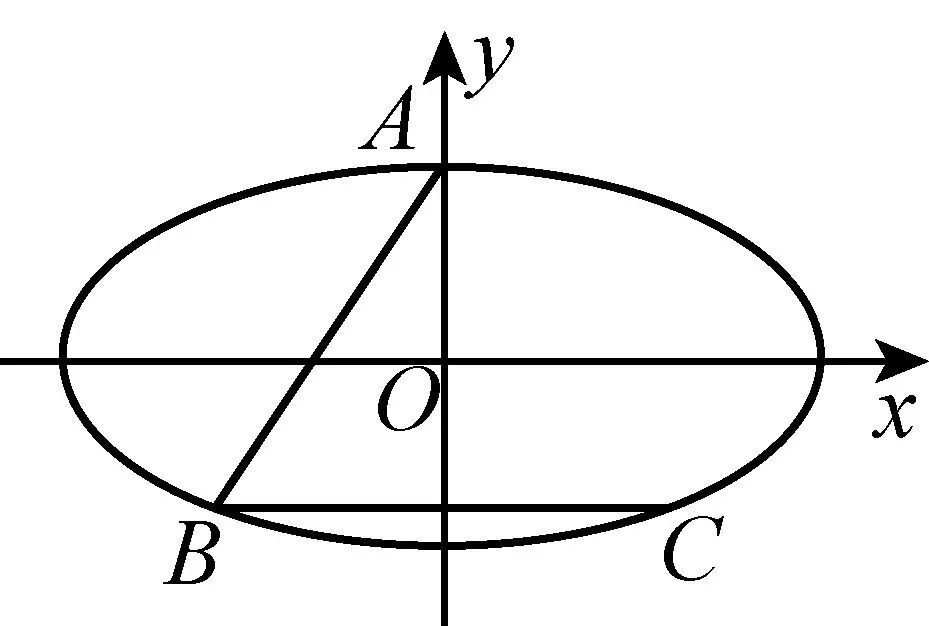
图6
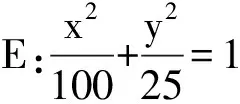
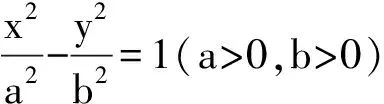
待学生尝试解决了三个问题后,归纳概括出解决解析几何中变量的取值范围(最值)问题的常见策略:
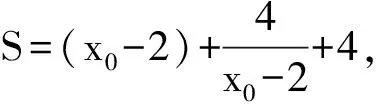
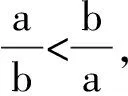
3个问题,方法各异,需要根据问题的特点,合理选择恰当的方法,学生在方法的比较中领悟各种方法的本质及适用的情境,从而实现突破瓶颈,以不变应万变.
总之,在解析几何一轮复习教学过程中,教师要以新课标理念为指导,转变教学观念,进行单元整体教学设计,重基础、重过程、重训练、重小结,注意站在学生的角度,想学生之所想,难学生之所难,疑学生之所疑,降低学生的认知难度,把课堂变成师生共同探索发现、共同提出问题、共同解决问题的阵地.从而使学生积极主动地学习,促进学生积极地参与课堂探究活动,让学生在亲身体验中了解数学知识发生、发展的过程,体会数学知识的应用价值,培养学习的兴趣,学会学习的方法,全面提高学生的数学素养.

