对排序不等式的教学理解
蔡佳宝 李 波 徐章韬
(华中师范大学数学与统计学学院 430079)
1 引言
排序不等式以其优美的对称结构著称,同柯西不等式一样是中学数学中的“重要而基本”的不等式.所谓“重要”,是指具有重大影响的,很有意义的.所谓“基本”,即根本,事物的本源.排序不等式的“重要”性不仅仅体现在它的应用方面,即由它可以推导出很多著名的不等式如:算术几何平均不等式、柯西不等式、切比雪夫不等式等,还体现在它是函数单调性证明的基础,是序结构的一种反映.序结构是布尔巴基学派运用结构观对数学进行分类时得到的一个母结构,它与代数结构、拓扑结构一起构成最普通、最基本的数学结构.从这个意义上来说,排序不等式又应是“基本的”.在进行排序不等式教学时,对教材的深入解读是必不可少的,若仅从证明的角度去理解排序不等式显然是不够的,作为数学教育工作者应该看到知识间的互通性与连贯性.下文从函数的单调性、向量、阿贝尔变换公式、微微对偶不等式等角度重新对排序不等式进行认识.
2 教学理解
2.1 看证明“基础”
设a1≤a2≤…≤an,b1≤b2≤…≤bn,k1,…,kn是{1,…,n}的任一排列,则

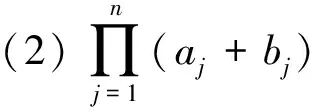
在用初等方法进行排序不等式证明之前,不妨先看例1的证明.
例1若a1≤a2,b1≤b2,则a1b1+a2b2≥a1b2+a2b1.
通过作差法显然有a1b1+a2b2-a1b2-a2b1=(a1-a2)(b1-b2)≥0成立.以此为基础,利用逐步调整法进行和排序不等式与积排序不等式的证明,实际上就是反复利用例1的证明过程.例1的证明过程是用逐步调整法证明排序不等式的一个“基础”.
(1)和排序不等式的证明

即为顺序和;当kj≠j时,存在某个aj0≠aj与bj搭配,现在调换bkj与bj的位置,于是原式Sn中的ajbkj+aj0bj通过调整变成了ajbj+aj0bkj,其余n-2项不变,两式相减,令
T=ajbj+aj0bkj-ajbkj-aj0bj
=(aj-aj0)(bj-bkj),
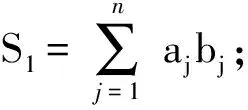
(2)积排序不等式的证明
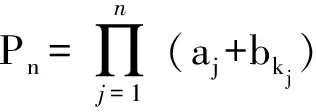
通过上述证明过程,不难发现,对于任意的x1≤x2,y1≤y2,始终有x1y1+x2y2≥x1y2+x2y1成立,此式即为排序不等式的“原型”.特别地,它是和排序不等式取n=2时的情形,当x1=y1,x2=y2时,我们还可以得到基本不等式,和排序不等式是在上式基础上得到的推广.事实上,对于任意给定的两个递增数列{an},{bn},Sn,Pn的最值是确定的.只需通过有限次的逐步调整来找到最值即可.逐步调整法实质上是一种算法.这种证明方法从直观上“看不到”完整的证明过程,它依赖于学生的思维活动,是学生在头脑中完成的.由此可见,在教学中使用逐步调整法进行排序不等式的证明有助于学生计算思维和逻辑推理能力的培养.
2.2 看等号成立条件

要证明和排序不等式成立,实际上就是证明下式成立
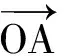
不妨先看n=2时的情形,
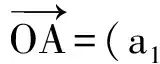
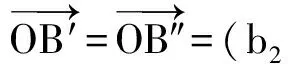
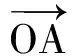
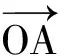
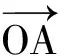
|OB|=|OB′|,cos∠AOB>cos∠AOB′,
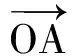
从向量的角度来看排序不等式,便于从几何直观上去理解排序不等式等号成立的条件.这种处理法类似于从向量的角度处理柯西不等式等号成立的条件.
2.3 从阿贝尔变换看
阿贝尔变换是指对一组乘积的变换.
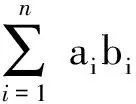
则
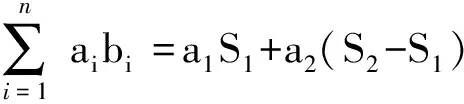
=anSn-anSn-1+an-1Sn-1+…+a2S2-a2S1+a1S1
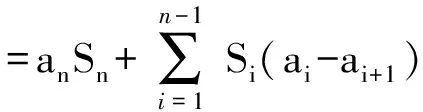
如果还嫌这个表达式难以记忆,画三个并在一起的长方形,长分别为a1,a2,a3,宽分别为b1,b2,b3,把面积算两次,自然得这个表达式.
现用阿贝尔变换证明正序和,乱序和,和反序和之间的关系.
不妨设ai≥ai+1,bi≥bi+1,
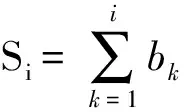
则有Sn=Tn=Rn,Si≥Ti≥Ri,
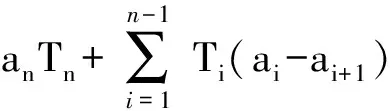

下面是利用阿贝尔变换证明排序不等式的另外一种方法[1].

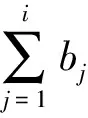
即Si≥Ti.
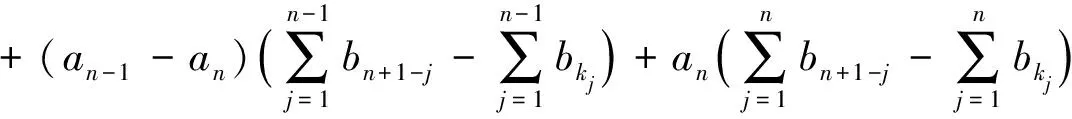
因此,对所有i=1,2,…,n,
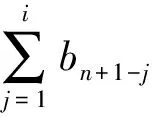
用高等数学方法证明排序不等式更简洁、明了.第一种证明方法是直接对不等式进行阿贝尔变换,而第二种证明方法则是先对所证不等式进行作差后再进行阿贝尔变换,究其实质都是在利用阿贝尔变换和单调性进行排序不等式的证明,这种方法相比起初等数学方法更直观、具体、能“看得到”证明过程.
2.4 看单调性
函数f(x)在区间D上是增函数,对于∀x1 单调性是函数的一种重要意义,用单调性证不等式是一种十分有效的技法.其根本原因在于用单调性证不等式,其实是在运用排序不等式,而排序不等式是序结构的反映,故单调性很基本,也很有用. 以三元排序不等式为例.把它们两两的乘积写成一个矩阵的样子, 很显然,主对角线上的元素之和是正序之和,副对角线上的元素之和就是反序之和.类似于三阶行列式的乘法,其它与主对角线、副对角线平行的位置上的元素之和就是乱序和.注意到矩阵中的所有元素之和为(a1+a2+a3)(b1+b2+b3). 一般地,可以列出不等关系 把这些式子相加,自然地就得到了切比雪夫不等式. 现在用排序不等式证柯西不等式. 由此得到矩阵的列积和为(a2+b2)(c2+d2), 由此得到矩阵的列积和为(ac+bd)2, 由微微对偶不等式,自然得到柯西不等式. 柯西不等式特殊化之后也能得到教材中的基本不等式. 现代数学学习理论认为数学有意义学习的实质是学习者能够将新知与认知结构中已有的适当知识建立非人为的实质性的联系.这意味着新知识在学习者的认知结构中有生长点或固着点,倘若教师在进行新知教学时能够帮助学生在原有的认知结构中找到新知的固着点,这无疑是有意义教学的前提.这也是奥苏泊尔所提倡的先行组织者策略.单调性是学生在学习函数时接触到的,因此单调性对于学生来说是十分熟悉的,用单调性证明不等式实质上是在运用排序不等式,倘若以此作为学生学习排序不等式的生长点,那么学生对于排序不等式的学习就不会感到陌生.这样可以帮助学生建立起单调性与排序不等式之间的联系,理解序才是单调性的基本,从而更深层次地理解单调性的意义.进一步地,教师可以引导学生思考三维排序不等式的情形,最后再考虑更为一般的情形,逐层递进,步步深入,引导学生进行思考,这种从特殊到一般逐渐抽象的思维过程有利于提高学生的抽象思维能力.这和柯西不等式的教学思路是一致的. 习得直观图景是数学教育的目标之一.本案例让学生看到,在维数上,排序不等式和柯西不等式一样,有二维、三维,乃至多维的情形,可以仿照柯西不等式来学习;在实质上,排序不等式反映了函数单调性,并把其推向了一般,是函数单调性的进一步抽象;在证明基础上,排序不等式的证明基础是阿贝尔变换,这其实是一种面积法.在知识生长上,微微对偶不等式是排序不等式矩阵形式的进一步推广.数学的眼光是抽象,但这种眼光的高境界是一种直观、一种直觉,一种不用“眼睛”的“眼睛”. 当数学从科学形态转变成教育形态时,便形成了数学教育.数学教学具有很强的专业性,它体现在两个方面,一个是“数学”方面,一个是“教学”方面.没有一定的数学修养的教师是不可能教好数学的,同样,有数学修养但没有一定的教育教学理论的教师也是教不好数学的.这就要求教师深入钻研和分析课程标准、教材、教学辅助资料以及相关数学史的研究等,理解和掌握教学内容.另一方面,数学教育究其根本是要育人,这就必然要求数学教育工作者具备一定的教育教学理论.数学本就以“抽象”著称,若教师不了解学生的学习心理,就容易给学生造成数学太抽象、不好学之感.因此教师需要用“两条腿走路”,既要不断提高自身的数学修养,又要不断提高自己的教育教学理论水平.这两方面能力的提高是相辅相成的.教师自身数学修养的提高,有助于教师对知识本质的理解,才知道“教什么”,而教育教学理论水平的提高有助于教师了解并理解学生,才知道“怎么教”.这就要求教师从不同视角,多角度去把握所授内容.不仅要看到初等数学与初等数学之间的联系,更要看到高等数学与初等数学之间的关联.从初等数学的角度去看初等数学,有助于教师找到知识之间的联结以及学生的认知起点.从高等数学的角度去看初等数学,有助于教师加深对知识本质的理解,掌握知识的“来龙去脉”,建立知识团,进一步理解所授知识的教育意义和价值.2.5 看生长性


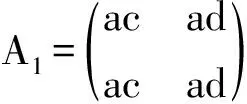

3 总结

