法随心动 心由境生
——由一道数学题的解法探究产生的若干思考
蒋 凯 钱云祥
(1.苏州胥江实验中学 215004; 2.无锡市蠡园中学 214072)
数学解题,解法往往千变万化.也就是说,一道试题,也许存在许多种不同的解法.这些解法究竟都是怎么想到的呢?也许是经验,也许是感觉,也许是运气.笔者认为,经验需要实践来积淀,感觉其实就是经验的一种看似有点模糊的成功体现,而运气则需要感觉作支撑.在对问题的解法进行探究之时,往往法随心动,心由境生,即法是偶然的,心是自由的,境是客观存在的.面对实际的数学问题,解题者即时产生的灵光一现,常常就能形成一种解法.而这些即时性的想法,往往又带有一定的偶然性,故而也就出现了一题多解.在日常教学中,无论是对于教师,还是对于学生,对问题的研究,其实毫无必要陷入题海,对一两个问题的深度研究,往往即可形成与积淀有效的解题经验.
试题呈现
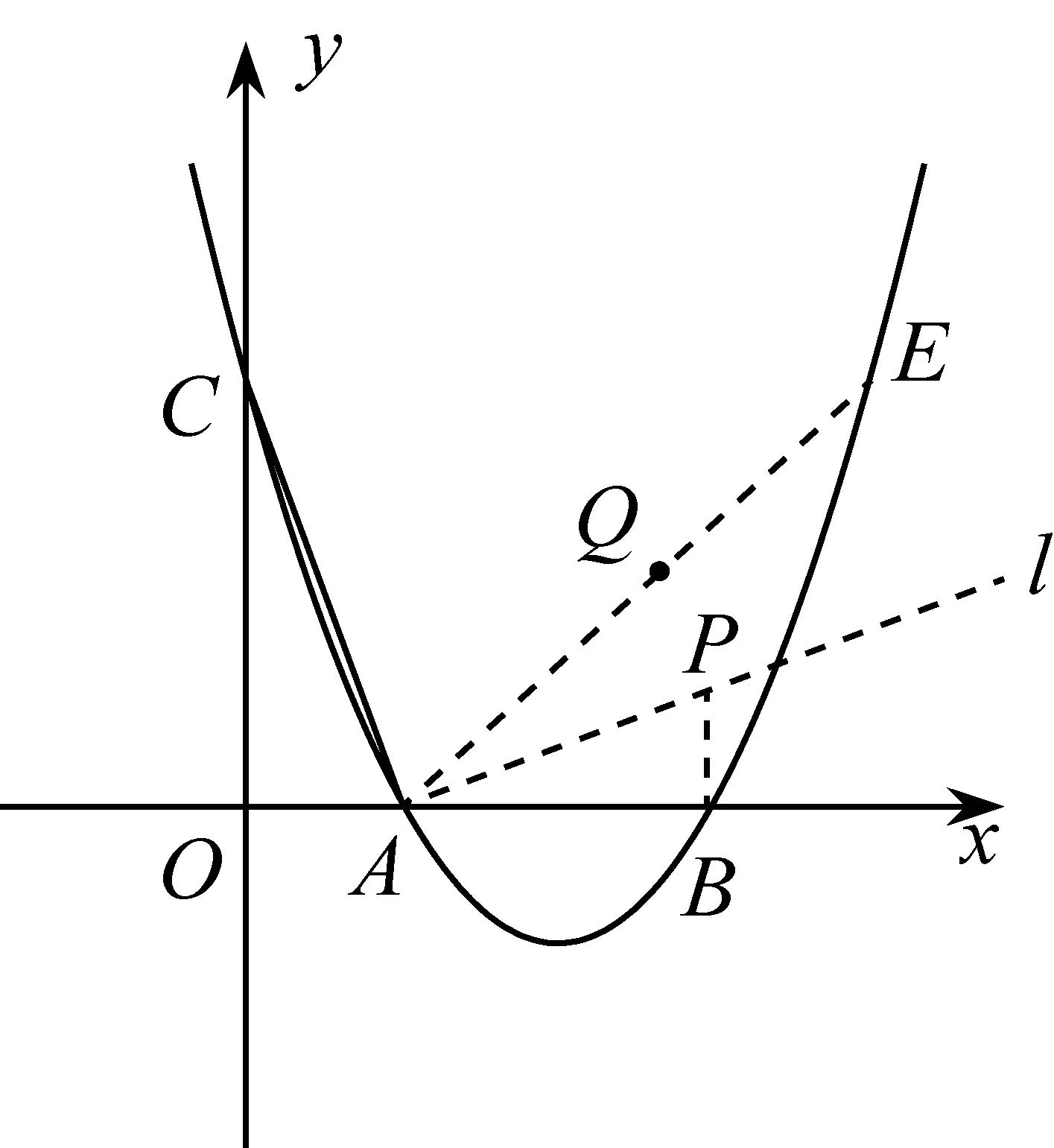
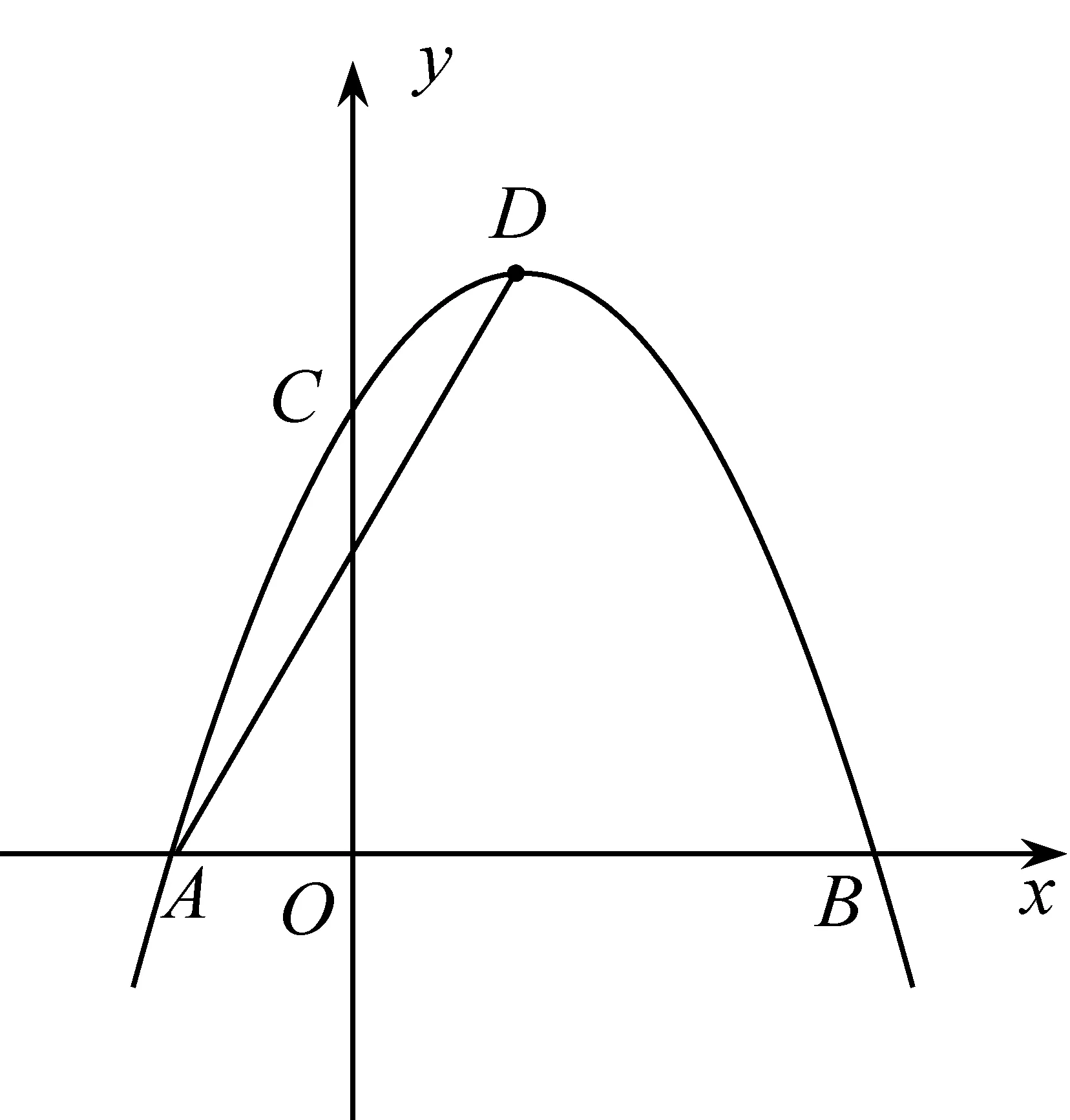
如图1,二次函数y=mx2-4mx+2m+1的图像与x轴交于A(x1,0)、B(x2,0)两点,与y轴交于点C,且x2-x1=2.
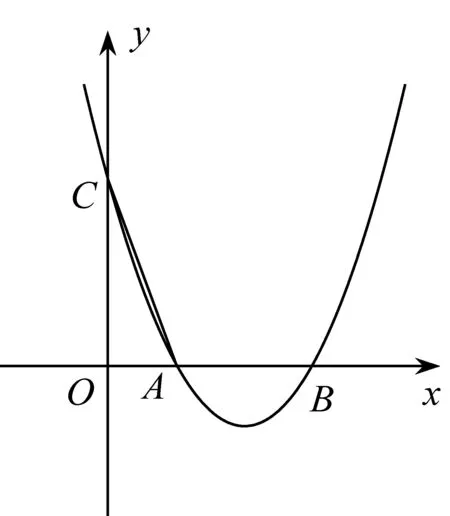
图1
(1)求这个二次函数的表达式;
(2)若E为这个二次函数的图像上一点,且∠EAB=2∠OCA,求点E的坐标.
问题初探
第(1)小题思路较为简单:不难确定二次函数y=mx2-4mx+2m+1的图像的对称轴为直线x=2.由题意知,这个二次函数的图像与x轴的两个交点之间的距离AB=2,故A(1,0)、B(3,0).把x=1,y=0代入y=mx2-4mx+2m+1可得m=1.所以这个二次函数的表达式为y=x2-4x+3.
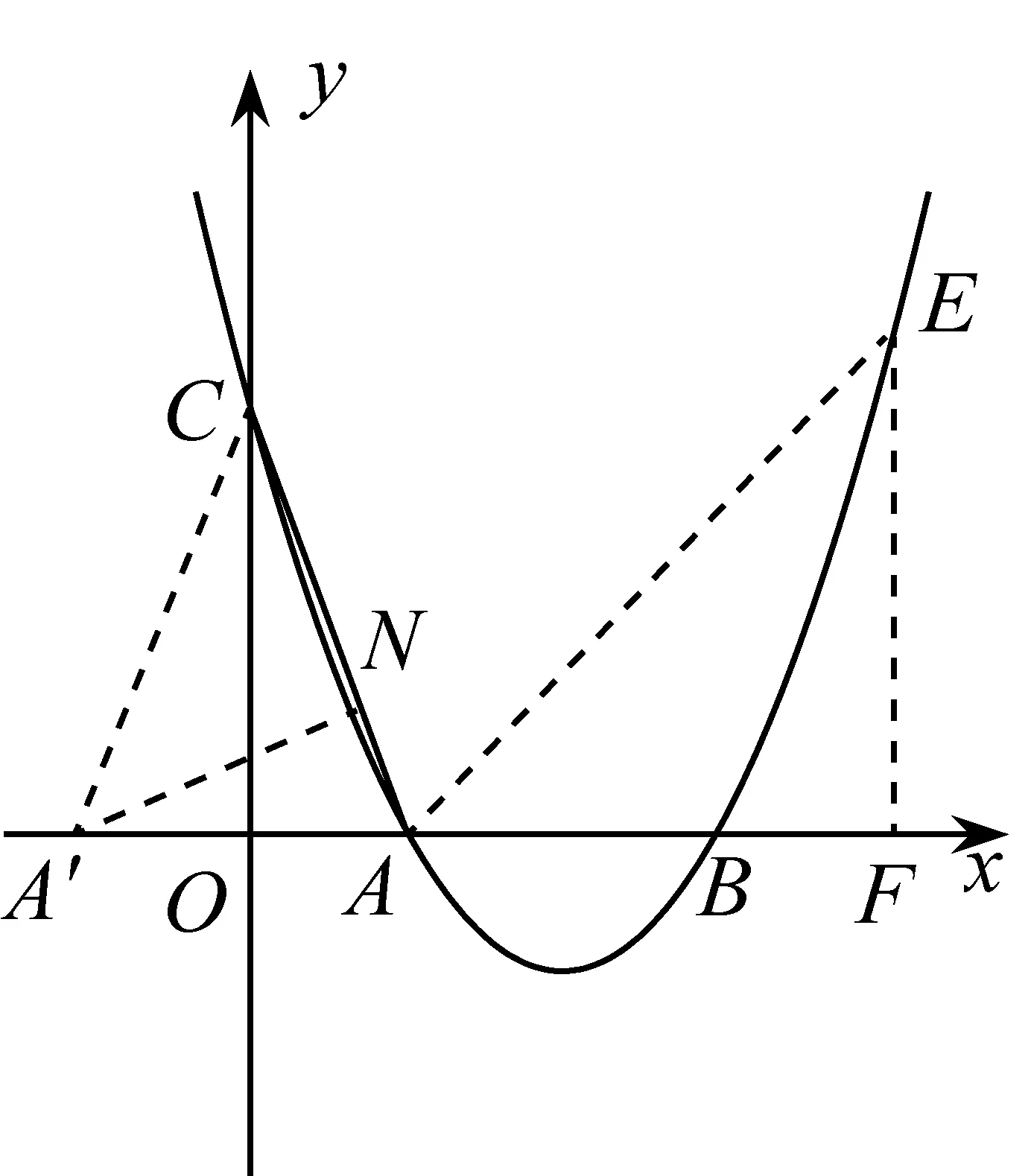
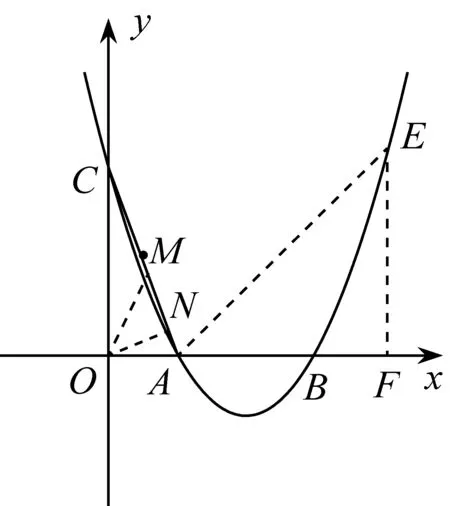
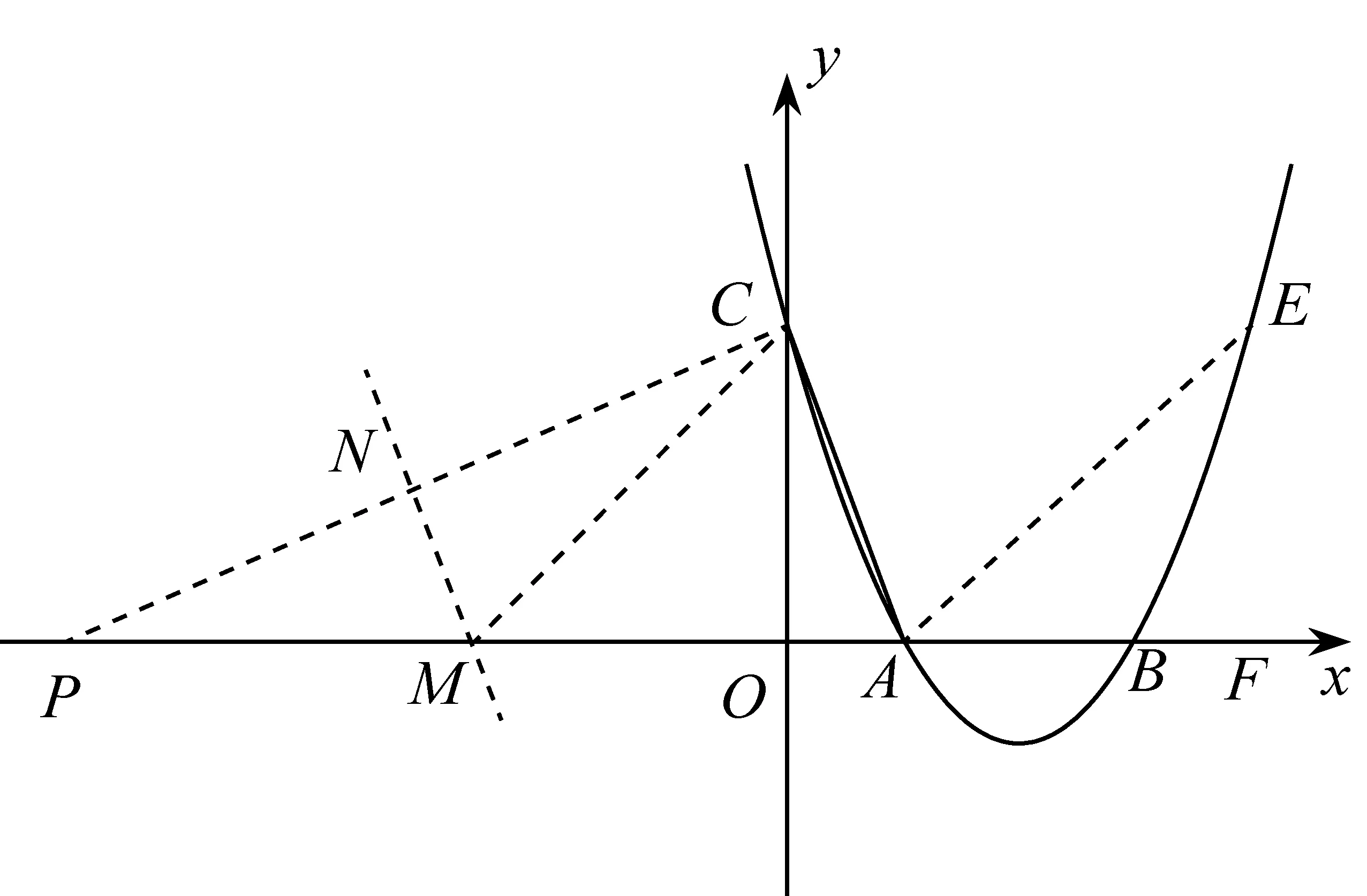
在对第(2)小题分析时,显然,C(0,3).结合A(1,0),可知OA 分析问题,可以看出,解题的突破点在于对点E所满足的条件“∠EAB=2∠OCA”的信息挖掘与利用.显然,图中不存在现成的角,使得其大小恰为2∠OCA,故需考虑构造,然后在此基础上确定点E的坐标.怎样构造?需放飞思绪,不同的想法产生不同的解法. 思路1如图2,可以作出点O关于直线AC的对称点M并求出其坐标,然后连接AM并延长交二次函数的图像于点E,则点E满足∠EAB=180°-∠OAM=180°-2∠OAC=2(90°-∠OAC)=2∠OCA.事实上,这种思路的出发点就是考虑构造∠OCM=2∠OCA,再构造∠EAB=∠OCM,故∠EAB=2∠OCA.此外,设点M关于x轴的对称点为M′,不难求出直线AM′与二次函数的图像的另一点E′的坐标,若点E′在点A的右侧,则符合题意,否则第四象限内的函数图像上就不存在符合题意的点. 图2 思路2如图3,作点A关于y轴的对称点A′,连接CA′,则∠ACA′=2∠OCA.接下来只要构造∠EAB,使其等于∠ACA′.具体怎么构造?似乎有点难度.考虑到确定点的坐标一般要构造直角三角形,所以可以设法构造一对相似的直角三角形:如图4,过点A′作A′N⊥AC于点N(构造Rt△A′CN).设第一象限内二次函数图像上的一点E符合条件,连接AE,过点E作EF⊥x轴于点F(构造Rt△EAF),易证△A′CN∽△EAF,然后根据“相似三角形的对应边成比例”可求出点E的坐标……同样地,也可利用构造一对相似的直角三角形求出第四象限内满足条件的点E′的坐标,或者,利用对称性先求出直线AE关于x轴的对称直线所对应的函数表达式,再联立方程组从而求出点E′的坐标. 图3 图4 图5 比较上述几种思路,我们可以发现,思路1与思路2都是在∠OCA的基础上构造一个角,使其等于2∠OCA,而思路3则是先构造∠PAB=∠OCA,然后在∠PAB的基础上进行相关构造……最终殊途同归. 上述三种思路的共同之处,都是通过“翻折”构造二倍角.那么,除了“翻折”之外,还有没有其他常见的构造二倍角的方法呢? 思路4如图6,取AC的中点M,连接OM,由于∠AOC=90°,故OM=CM,∠MOC=∠MCO,所以∠OMA=∠MOC+∠MCO=2∠OCA.接下来只要构造∠EAB,使其等于∠OMA.如图7构造一对相似的直角三角形,具体解法与思路2类似.限于篇幅,不再赘述. 图6 图7 图8 …… 图9 不同的念头,产生不同的解法.当然,对于问题的解法探究,作为教师,在实际教学中毫无必要无休无止地一味追求解法的多样性;同样地,作为学生,在学习过程中也没有必要对每一道题目都想法设法采用不同的方法去分析、解决.但是,我们知道,不同的学生,其思维习惯与思维品质是有差异的.其中,有些是有优劣之分,但也有很大比例其实并无优劣之分.换句话说,有些解法的差异取决于学生的思维品质差异,而有些差异则取决于学生的即时心理反应.之所以说法随心动,正是因为心之所向,身之所往.也就是说,在数学解题的实践中,有了内心的想法与向往,行动自然也就有了或模糊或清晰的方向.所以说,数学强调思维,学习数学,能让人变得越来越聪明.在对上面问题的分析与解答中,不同的思路就源自于不同的心理活动.事实上,上述不同思路,正是笔者的一次真实课堂教学实录.课堂上,学生尽情地表达自己的真实想法,尽情地流淌出即时的思维火花…… 法随心动,那么心又如何动呢?我们知道,数学问题的解法探究讲究自然生成.在解题的过程中,当面对问题情境时,不同的学生,其视角是不同的,相应的想法自然也就不同了.此外,不同的学生,其已有知识储备水平尤其是解题经验的积淀基础是不一样的,这样就造成了他们审题之后头脑中即时形成的解题计划会有明显的差别.所以说,法随心动,心由境生.从某种程度上讲,解法的形成既是自然生成的,也是讲缘分的. 我们不妨再回到上述问题的不同解题思路上来进行分析:思路1和思路2,这两种想法的出发点,都是基于∠OCA,通过翻折构造2∠OCA.而思路3则先将∠OAC转换成∠PAB,然后基于∠PAB通过翻折构造2∠PAB.孰优孰劣?很难作出恰当的评判,完全看学生的即时心境. 再如,思路4是利用“直角三角形斜边上的中线等于斜边的一半”这一性质构造已知角的二倍角,但后续解法则与思路2相同.同样是构造二倍角,思路5、思路6则是借助“线段的垂直平分线上的点到线段两端的距离相等”这一性质进行构造,相比于图7中的∠OMA,图8中的∠OMA及图9中的∠OMC明显“好”多了,因为图8中的∠OMA及图9中的∠OMC各有一边落在坐标轴上,这样就为后面的进一步构造带来了极大的便利.尤其是思路6,“过点A作AE∥CM”,则直线AE与CM所对应的函数表达式中x的系数相同,即斜率相等.如此一来,后续解答中就省却了再进一步构造一对相似的直角三角形,然后利用“相似三角形的对应边成比例”进行求解. 俗话说,仁者见仁,智者见智.不同的心境产生不同的灵感.即使对同一个问题,不同的人从不同的立场或角度去看也有不同的看法.正因为如此,所以许多数学问题,其解法往往是多样的.一方面,我们没有必要去追求解法的一致性.异彩纷呈的多样解法,岂不正是培养学生创新思维的良好契机?思维的灵动,需要合适的环境与土壤.这种环境与土壤,不需要刻意地去打造,但却需要教师恰到好处的培育与呵护.另一方面,在课堂教学的现场,当多样解法或如约而至或不期而遇之时,其实倒也提供了思辨的绝佳素材,同时也是引发学生进一步深层探究的导火索. 从教师角度看,应确立这样一个观点:最好的解法绝不是教师事先设计出来的,而是学生最容易想到的,是课堂自然生成的.所以,教师在课堂上应营造一种民主平等的教学氛围,要让学生敢于自由表达自己的真实想法,哪怕是一些很不成熟的一闪而过的念头.这种理念支撑下的教学,将充分彰显课堂的活力与魅力,因为课堂的真实,能给教师和学生带来一种真实的享受. 从学生角度看,不能仅停留在“得到一道题的答案”这一层面的自我要求上,而应善于思索“解法到底是怎么想到的”.只有这样,才能不断形成、获取与积淀解题经验,从而形成一定的解题策略.此外,还要善于主动表达与理性对比分析不同的解法,以探寻成功解题的共性,进而不断地在实践中提升解题的信心. 经验的获得虽然带有一定的随机性,但却又是可移植的.同时,一次次的成功体验,对学生学习信心的获得与提升,也大有裨益.对数学问题的每一次思索,未必一定能得出一种可行的解法或成功的思路,但是要坚信,对问题的深度思索,一定能促成对问题的更好理解,一定能给解题者带来新的解题方向的启示. 练习:如图10,已知二次函数y=-x2+2x+3的图像与x轴交于A、B两点(其中A在B的左侧),D为顶点,P为x轴上一点,设∠DAO+∠DPO=α,若tanα=4,求P点的坐标. 图10 分析问题,不难求得图中A、B、C、D四点的坐标分别为A(-1,0)、B(3,0)、C(0,3)、D(1,4).在此基础上,要确定点P的坐标,关键在于能否有效挖掘条件“tanα=4(其中α=∠DAO+∠DPO)”的价值.带着对问题的进一步思考,也许会产生许多新的思索:(1)α大概有多大?(2)符合条件的点P应该有几个?(3)∠DAO与∠DPO的和能不能转化为某一个角?(2)图中有没有哪个角的正切值恰好等于4?……诸如此类问题,必将促成心由境生、法随心动,其结果就是问题逐渐变得明朗. 解题研究,无论是对教师而言,或是对学生而言,都很有必要.面对一道陌生的试题,需要用心地咬文嚼字般地审题,需要结合相关条件在头脑中快速搜索曾经获得的解题经验与策略,需要不断尝试……期间,每个人对试题中的每一个信息的解读都是有差异的,所以,不同的人审题后的心理变化也是不一样的.但是,我们不应也不必过度担心自己的思路可能行不通而不愿尝试.事实上,一方面,可行的解题方案未必是唯一的,不尝试又怎么知道自己的想法一定不可行呢?另一方面,只有“敢想”才会逐渐走向“能想”、“会想”.用敏锐的眼光去审视问题情境,以丰厚的经验积淀为基石,放飞思绪自由驰骋,相信自己,一定能在实践中找寻到走向成功的解题密钥.法随心动

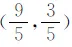

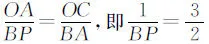



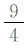
心由境生
触类旁通
感悟提升

