数学解题教学要引领学生走理解之路*
——一次自习辅导课学生的意外“落水”与教学设计及思考
刘亚平 黄晓学 赵 波
(1.江苏省睢宁高级中学 221200;2.江苏师范大学教育科学学院 221116;3.江苏省睢宁李集中学 221221)
通过高三数学一轮复习,学生解题的思路已形成、方法已具有、思想已领会、思维已优化.然而,时常会出现令人费解的一幕:教师认为应该做得很好的题,学生却做得不尽人意.下面通过一道试题的教学来一探究竟.
1 试题的呈现
已知函数f(x)=a(2-x)ex,g(x)=(x-1)2(e为自然对数的底数).若关于x的方程f(x)=g(x)有两个不相等的实数根x1,x2,求实数a的取值范围.
这是一位高三学生在数学自习课上独立研究的一道试题,该题条件简洁,但高度抽象、内涵丰富、综合性强,涉及分类讨论、转化与化归、数形结合、函数方程等思想,考查函数零点、构造法、分析法等知识与方法.该学生说,虽然题后有详细的解答过程,但仔细研究后仍对某些细节感到困惑、多次被迫“落水”,让学习者很“痛苦”.于是,笔者决定采取一对一指导教学模式,探究学生因何缘故多次“落水”.
2 教学设计及意图
2.1 选择转化,准备“搭桥”
问题1已知f(x)=g(x)有两个不相等的实数根x1,x2,你能直接求出此方程的两个根吗?如果不能求出方程的根,那又如何处理?
设计意图学生遇到方程根的问题,第一反应可能是想把方程的根直接求出来,由于f(x)=g(x)是超越方程,没有固定的求根公式,显然强攻硬取是不明智的.既然求不出方程的根,那必须用转化思想把方程根的个数转化为相应的函数零点个数,看看学生有无转化意识.
学生:因为f(x)=g(x),所以(x-1)2-a(2-x)ex=0有两个不相等的实数根x1,x2,由于此方程是超越方程,通过尝试也无特殊值的根,所以无法直接求根.对于类似问题,运用函数、方程思想转化为函数h(x)=g(x)-f(x)在R上有两个不同零点.
2.2 找准方法,准备“过河”
问题2已知函数零点的个数,求参数的取值范围.有几种常见的研究方法?如何运用这些方法?对问题1你选择哪种方法?
设计意图学习数学需要一定的记忆与模仿,不单单是归纳、理解与反思.数学概念、定义、定理、基本方法、基本技能等该学生记忆与理解的,教师就要不耐其烦地反复渗透,直到学生耳熟能详为止.
学生:有四种方法:1求方程的根;2零点存在性定理;3构造一个函数;4构造两个函数.方法1与方法2实质是函数零点定义;运用零点存在性定理需要满足两个条件:一是连续函数;二是函数在区间端点函数值异号;构造两个函数时,两个函数图象有几个交点原函数就有几个零点,交点的横坐标就是原函数的零点.另外,在构造两个函数时,使用参变量分离法时尽量使构造的两个函数中一个为常函数或一次函数,这样便于画图.解决本题我选择方法3与方法4.
2.3 踏着“险桥”,被迫“落水”
问题3请你把解题过程写出来,解题中涉及哪些思想方法?你有哪些困惑点?
设计意图困惑产生问题,问题来自困惑.有时候,提出问题比解决问题更弥足珍贵.只有让学生亲身经历解题过程才能提出真问题,这有利于教师准确把脉学生解题思维的困惑点.
学生:解题过程用到分类讨论、数形结合等思想,解题中我有三个困惑点.
因为函数h(x)在R上有两个不同零点,所以h(x)的图象与x轴有两个不同交点.
因为h′(x)=2(x-1)+a(x-1)ex
=(x-1)(aex+2),
①当a=0时,h(x)=(x-1)2只有一个零点x=1,故a=0不成立;
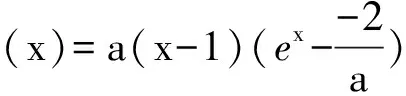
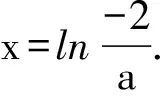
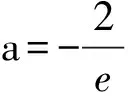
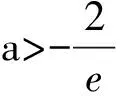
所以函数h(x)在R上只有一个零点;
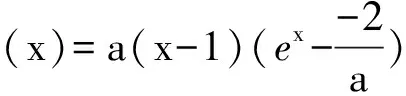
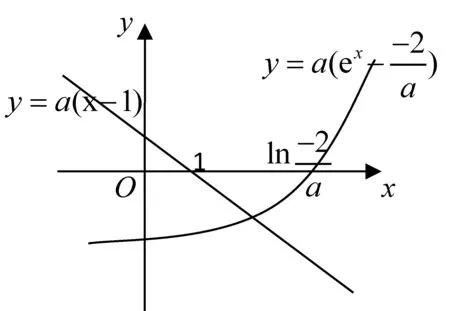
图1
③当a>0时,h′(x)=(x-1)(aex+2),令h′(x)=0,得x=1.
列表判断得h极小值=hmin(x)=h(1)=-ae<0,根据函数h(x)的大致图象可以判断有两个零点(如图2).

图2
但判断h(x)有两个零点时,学生又遇到两个困惑:一是因为h(3)=ae3+4>0,所以h(1)·h(3)<0,又因为h(x)在(1,+∞)为单调递增连续函数,所以由零点存在性定理知h(x)在(1,+∞)有一个零点,同样也可以取h(4),h(5),……,为什么这些值都大于0,难道仅仅是巧合?
二是为什么h(-4),h(-5),……,符号不确定?如何在(-∞,1)上取值才能使其函数值大于零?
2.4 数学经验,辅助“过河”
问题4.1我们在画函数p(x)=a(2-x)(a∈R)的图象时,能否任意画?理论依据是什么?
问题4.2在刚刚过去的月考中,我们解决过一个类似问题:已知函数f(x)=ex+m(x+1),其中m<-1,e是自然对数的底数.求证:f(x)在R上有两个零点.大家当时是如何运用零点存在性定理判断零点的?
设计意图普通高中数学课程标准明确提出要培养学生的四基,即培养学生的基本知识、基本技能、基本思想与基本活动经验.对于学生提出的上述两个困惑点,教师通过激活学生已有的活动经验启发学生深度思考.

教师追问:能否再举出其他函数值大于0,学生回答:f(-3m),f(-4m),……,函数值都大于0.因势利导,教师接着问道:为什么f(3),f(4),……,甚至f(100)=e100+101m的函数值不一定大于0?学生思考交流:因为m<-1,所以从f(100)=e100+101m解析式本身就能看出函数值不一定大于0;又因为极小值点ln(-m)能取遍一切正数,更能诠释f(100)的函数值为什么不一定大于0.
2.5 积累经验,成功“上岸”
问题5我们来继续探究问题3中尚未解决的问题:如何在(-∞,1)上取值才能使其函数值大于零?
设计意图在学生合作交流与情感体验中积累数学经验后,通过问题5培养学生的知识方法迁移能力,领悟取值方法——放缩法.
学生:因为a>0,所以h(-4)=25-6ae-4符号不确定,因此不能在(-∞,1)取确定数的函数值,若取x=b(b<0),h(b)=(b-1)2+a(b-2)·eb,但我不知下一步如何放缩?
教师:h(b)=(b-1)2+a(b-2)eb(b<0)是关于b的超越函数,能不能通过放缩把它变为关于b的基本函数?
学生(恍然大悟):让我试一试,h(b)=(b-1)2+a(b-2)eb>(b-1)2+(b-2)=b2-b-1,但b2-b-1>0对一切b<0不成立,学生通过多次尝试,终于放缩函数值成功,并给出取值理由.
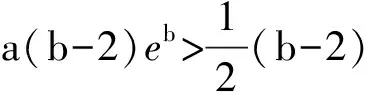
教师追问:还有其他放缩方法吗?你能否给出更一般的放缩方法?在教师的循循善诱的引导下,学生探究如下:
取b<0,不妨设h(b)=a(b-2)eb+(b-1)2>λ(b-2)+(b-1)2=b2+(λ-2)b+(1-2λ),其中λ>0,要使p(b)=b2+(λ-2)b+(1-2λ)>0对一切b<0成立(如图3).
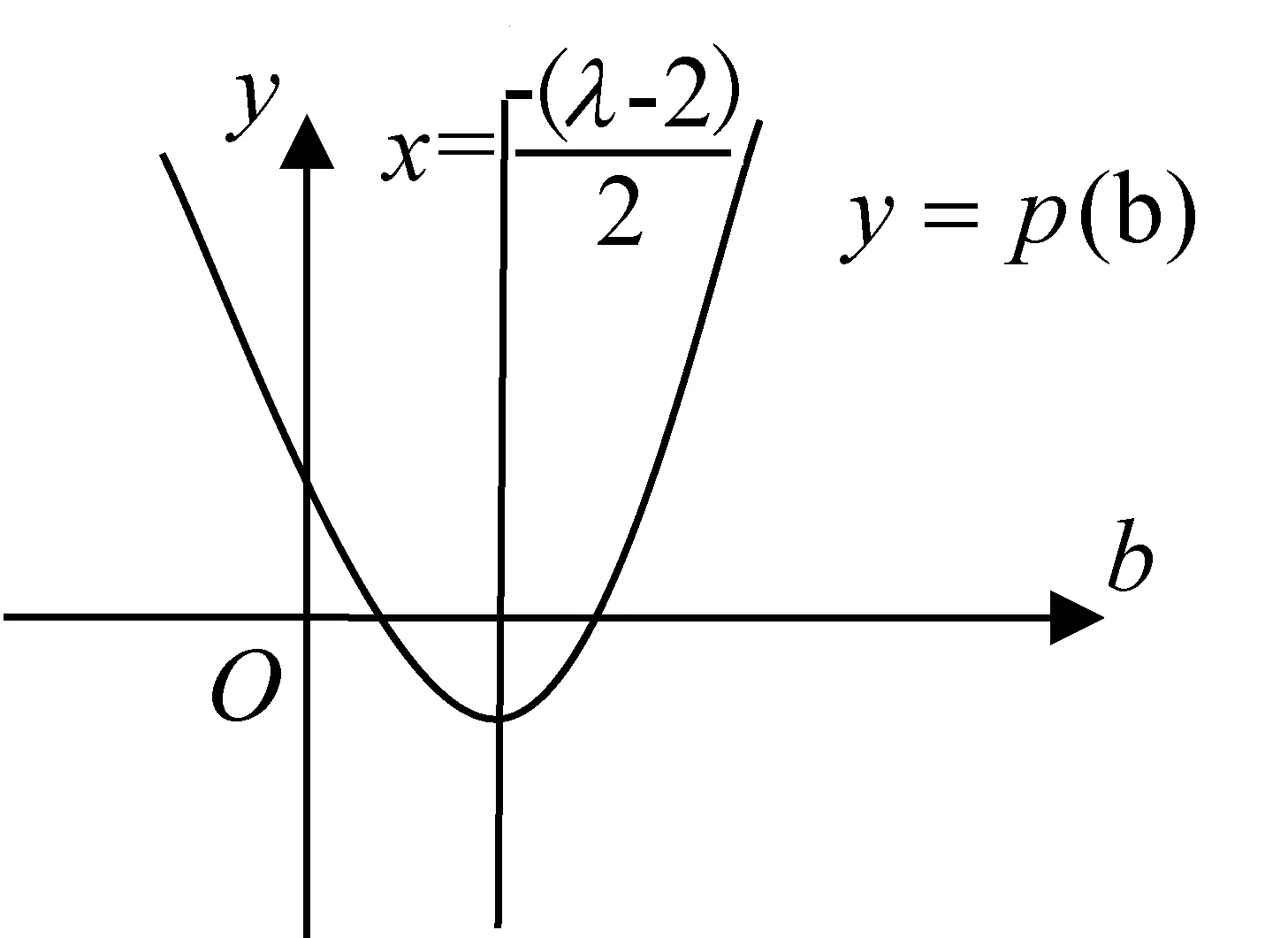
图3
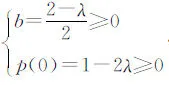
2.6 顺流而下,再探优法
问题6你能给出更简洁的解法吗?并指出这种解法的优缺点.
设计意图考查学生的转化与化归、数形结合等思想,甄选优法的能力.
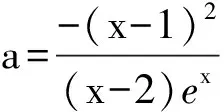
3 思想“缺失”,再次“落水”
听到学生对选择构造两个函数法“真实”的缘由,笔者又让学生解决如下问题.
(2015年江苏省高考数学第19题)
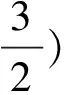
设计意图创设认知冲突,让学生深刻地认识到注重通性通法及挖掘题设中蕴含的数学思想方法,才是解决数学问题的“正道”.
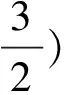
4 教学思考
理解数学、理解学生、理解教学是教师专业发展的基石,是数学教学质量的根本保证,是广大数学教师提高教学效益的法宝.学生是学习的主体,理解学生教师可以准确地找到学生的“潜在思维发展区”,调动学生学习的积极性,让学生觉得知识的发生、发展自然而徜徉,进而更好地理解数学.如何引领学生走上数学解题教学理解之路呢?本人有如下三点的思考.
4.1 解题内容的设计要关注学生的理解
现在高三数学复习课流行这样一个模式:三个例题、几个变题、一系列训练题,数学复习课俨然成了数学题目的堆砌课.教师一开始就滔滔不绝地忙于分析讲解、规范展示,学生忙于听讲记录,积极思考!但一考试,学生的成绩就让师生“苦恼不已”.理解性教学认为,教师在关注三维目标教学时,更要关注建构学生的理解能力,而不仅仅是解法的获得与思维的提炼,要急学生所急,想学生所想,惑学生所惑,需学生所需,才会真正设计出适合学生思维发展需要的“真内容”.
由于试题1有详细的解答过程,学生仔细研究多遍,教师在与学生的交流讨论中,没有发现学生在数学思想方法方面有太多的认知障碍.但在“顺流而下,再探优法”的教学环节中,构造两个函数法优点是构造函数中不含参数,不需要分类讨论,竟然成为这位学生“情有独钟”此方法的最主要的理由.涉及函数零点问题的通性通法主要有四种,至于运用哪种方法好,要因题而异,学生仅仅凭借“感情用事”,显然学生的理解方向出现的偏差.
关注到学生的理解,遵循“顾客是上帝”的服务原则,笔者设计了试题2,使学生产生“不愤不启、不悱不发”的强烈的释疑愿望,学生在特定的情境中,用自己的头脑去发现解决问题的办法,为学生发现新方法和认识新思想创造了一个最佳的心理环境.毋庸置疑,一个恰当的例题胜过一打理论,也胜过“结构松散”的多道例题的讲解与示范.
4.2 解题活动的设计要促进学生的理解
著名国学大师王国维在《人间词话》中对诗人的最高境界给予精辟的描述:“诗人对宇宙人生,须入乎其内,又须出乎其外.入乎其内,故能写之;出乎其外,故能观之.”同样,最高境界的数学解题教学何尝不是如此呢?入乎其内,就是要鼓励学生亲力亲为的实践,从自己砥砺前行的探索思考中获得体验,通过积极思考、动手操作、自主探究、合作交流等学习方式,慢中求悟、悟中求道;出乎其外,就是学生通过丰富多彩的数学问题的顺利解决觉得“数学好玩”,能感悟“题在书外,理在书内”的深刻道理,对数学本质的理解大彻大悟.
在教学过程中,笔者根据对学生的已有认知进行了分析,所设计的学习活动紧紧围绕学生理解的思维生惑点进行.江苏师范大学黄晓学教授在其《少教多学模式研究》中指出:“‘惑’这种心理现象在数学教学中主要发生在学生遇到数学知识发生发展的生长点和衔接点、数学思想方法的转折点、数学思维的症结点等时机.这些关节点、转折点、症结点都是典型的思维生惑点.并进一步指出,这些思维生惑点的解除必须通过发展认知能力才能实现”[1].为了帮助学生顺利突破思维生惑点,教师要适时帮助学生解释困惑,支撑学生的理解.
例如,对于第一个困惑,教师通过引导学生学会作图方法(一个坐标系内画两个函数的图象)解除学生的困惑;对于第二个困惑,根据函数h(x)在区间[1,+∞)为单调递增函数,且h(x)恒过定点(2,1),学生容易理解;对于第三个困惑,教师并没有把取值方法强塞于学生,而是借助学生已有的数学活动经验,从另外一个角度进行再回顾,给学生带来新鲜感,促进学生从多个角度思考问题,学生再次感悟放缩法取值的真谛,使学生获得真正意义上的理解,实现知识的正迁移.
4.3 解题评价的设计要落实学生的理解
对数学解题教学的评价,是数学教学的重要一环节,但往往被部分数学教师所忽略.有的数学教师仅通过学生解题方法的优劣来评价学生;有的是通过学生对数学知识与方法收获多少来评价学生;更有甚者只是通过学生作业、反应快慢、考试成绩的多少来评价学生等.其实数学解题教学的评价既要评估学生掌握数学知识和技能的状况,又要考量学生的提出、解决问题的能力和思维发展状况,还要关注学生学习的情感、态度与价值观的取向.数学知识的获取不仅取决于学生的智力,还与学生的学习态度、学习习惯、参与的积极性、努力的程度、内在的动力等密不可分.教育家苏霍姆林斯基说:“要像对待荷叶上的露珠一样,小心翼翼地保护学生幼小的心灵.”在数学教学时教师要对学生多一点耐心,多一点等待,多一点倾听,多一点激励性评价,学生就会多一点学习数学的信心与勇气,多一点对数学本质的挖掘与理解.
如“学生(恍然大悟):让我试一试,h(b)=(b-1)2+a(b-2)eb>(b-1)2+(b-2)=b2-b-1,但b2-b-1>0对一切b<0不成立,学生通过多次尝试,终于放缩函数值成功,并给出取值理由.”;“教师谆谆教导:可见,套题型、记方法不是学习数学的根本啊!那怎么办呢?”;“学生豁然开朗:真没想到运用函数、方程思想把‘不等式解集’向‘方程解集’转化后是如此的简单啊!”等等.不经意间,这些都调动了学生的探究热情,让学生觉得他是学习的主人,师生的情感得以沟通,和谐学习的氛围得以保证,学生的活力得以激发,学生的理解得以落实.
学生是主体,教师是主导,这个教学的双主体是内涵丰富的话题,双主体的基础是理解学生,数学解题教学一定要从理解学生做起[2].要做到理解学生,就要充分关注“学情”;其次是理解数学,就是教师要研读教材,窥探数学本质,从数学思想方法角度给学生一双睿智的“眼睛”;再次是理解教学,教师教学要从学生的认知规律出发,选择适当的教学方法,帮助学生给通性通法寻求一个合理合情的“辩护”,让学生体会优秀的解法是自然的、有人情味的.

