高考试题探“源”之例谈圆锥曲线几个结论的直接应用

云南 马孟华

课本是高考试题的“策源地”，从近几年的高考数学试卷中，总是能找出许多与教材中的例题相似或来源于教材的例题、习题改编的试题，这些试题考查的都是现行教材中最基本、最重要的数学知识和技能，所有方法也往往具有普遍性和一般性，即我们所谓的通性通法，这既体现了高考的公平公正，也对中学数学的教学进行有效的建议，所以每年高考试题给大家的感受都是“年年岁岁题不同，岁岁年年均相似”，每一年的试题都给人以似曾相识的感受.

1.高考试题源于教材、回归教材

纵观近十年来的高考数学试题，总能在试题中找到课本习题、例题的影子，有些高考试题甚至直接来源于习题或例题，有些高考试题来源于例题、习题的改编，而有些高考试题的结论、方法来源于课本，所以，在吃透课本例题、习题的基础上深入挖掘其潜能，举一反三，灵活变题、解题，就能在高考中立于不败之地.下面通过一些例子说明高考试题无论形式还是方法上很多都来源于课本，最终还可通过课本例题、习题引申推广出相关结论直接解题，达到“意想不到”的效果.

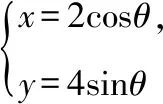
(Ⅰ)求C和l的直角坐标方程；

(Ⅱ)若曲线C截直线l所得线段的中点坐标为(1,2)，求l的斜率．

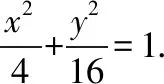
当cosα≠0时，l的直角坐标方程为y=tanα·x+2-tanα，

当cosα=0时，l的直角坐标方程为x=1．

(Ⅱ)【解法一】设直线l与曲线C交于A,B两点，将l的参数方程代入曲线C的直角坐标方程，整理得关于t的方程为(1+3cos2α)t2+4(2cosα+sinα)t-8=0． ①

因为曲线C截直线l所得弦AB的中点(1,2)在C内，所以①式有两个解，设为t1，t2，不妨设参数t1，t2分别为点A,B在直线参数方程中的参数，

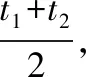
同时由于直线l恒过点(1,2)，故点(1,2)对应参数t=0，

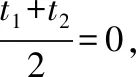
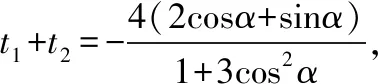
即tanα=-2，

故直线l的斜率k=tanα=-2．

该题的源头：人教版教材选修4—4:坐标系与参数方程第37页的例题2.

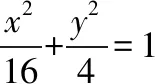
整理得(3sin2α+1)t2+4(cosα+2sinα)t-8=0，

由t的几何意义知|MA|=|t1|,|MB|=|t2|，

因为点M在椭圆内，这个方程必有两个实根，

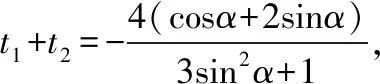
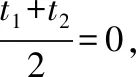
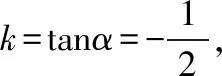
故直线l的方程为x+2y-4=0.

【评析】2018全国卷Ⅱ理科22题几乎完全采用了教材习题的解法思路来呈现高考试题，所以从根本上说明了高考试题源于教材，同时由于要兼顾其选拔功能，又将高于教材的出题思路体现的淋漓尽致.但此题的解法确实复杂了一些.一线的教学经验告诉我们，绝大多数学生对直线参数方程中的参数的几何意义是理解不到位的，只会单纯的解题，而忽略了参数方程的实际意义和应用价值，甚至如果出题时考虑将直线方程设置为非标准参数方程后，直线参数方程中参数的几何意义发生了变化，那么学生就更难解决这些问题了.如果我们不执着于此题的题型背景，在教材中寻找到更能被广大学生所接受的解决此类问题的方案，岂不更有价值和意义.

上述例题第二问如果抛开极坐标系与参数方程的题型背景，从直角坐标方程的角度直接分析，会有令人耳目一新的解法产生，解法如下：

【解法二】 设直线l与曲线C交于A,B两点，弦AB的中点为M(1,2)，设A(x1,y1),B(x2,y2)，则有

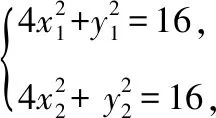
因为点M(1,2)为弦AB的中点，故有x1+x2=2,y1+y2=4，从而

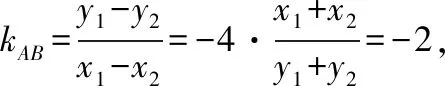
【评析】该解法完全抛开了直线参数方程中参数的几何意义的用法，而是采用了解析几何中处理圆锥曲线问题的常用手段——“点差法”.通过“点差法”建立了弦所在直线斜率和弦中点与坐标原点连线斜率之间的联系，这个联系就是解析几何中常用到的“中点弦公式”，值得注意的是该公式在近年来的高考中属于高频考点，在全国卷和各自主命题省份的高考题中频频出现，而其本身又是以教材例题、习题的形式出现的.可以看到，一方面教材的内容特点决定了高考的命题依据和走向，另一方面，高考的命题特点和规律又提醒我们回归教材，重新认知教材，二者相辅相成，相得益彰！教材就是高考试题的“根”，而高考试题就是在对教材的再认知、再探索中升华的产物.下面来看看此题中解法二的“根”在哪里.

人教版数学教材选修2—1第80页复习参考题A组中的第9题：

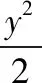
【分析】抛开该习题的“位置背景”(由于该题是教材2-1中圆锥曲线与方程后的习题，显然可以使用本章节的知识点解题，但这样就会束缚学生的思维)，如果是这样的习题作为“高考题”形式出现，那么考生在考场上就得各显神通了！其实作为高三复习备考的对象来讲，综合数学各方面系统知识可以知道此题有三种解法 .思考如下：

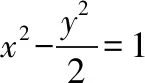
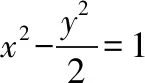
【小结】从以上几个教材例、习题与高考试题的对比分析中不难发现，高考试题源于教材又不局限于教材，它将数学中的系统知识融合起来，进行纵向联系，从而寻求最佳的考查数学思维的思路，而此时如果掌握了相关的已知结论就可以达到事半功倍的效果，不仅提升解题效率，而且还能培养学生的数学学科素养，下面我们就来谈谈解析几何中利用已知结论来提升解题效率的几个案例.

1.1圆锥曲线中的中点弦结论及其直接应用

若直线l与对称中心在坐标原点O的椭圆或双曲线交于两点A,B，且线段AB的中点为M，则直线l的斜率与直线OM的斜率存在以下关系：

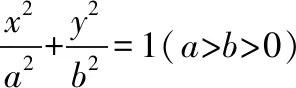
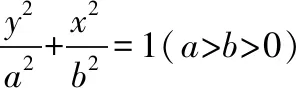
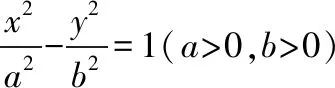
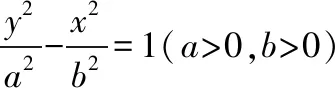
中点弦公式的推导方法常用“点差法”，此法也可以用于推导抛物线中与弦的中点有关的结论，如：

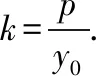
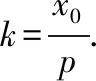
如果我们抛开上述结论的推导过程，直接将上述结论作为已知结论来用，那么在高考中将会大大提升解题效率.下面我们来看看几个源于教材又高于教材，同时利用已知结论快速解决问题的实例！

( )

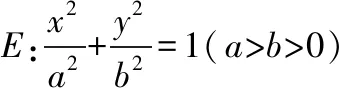
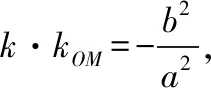
【评析】显然，如果使用通法求解，即联立直线和椭圆方程，利用韦达定理求解，则此题的难度就集中在了计算、化简上，这样将会浪费大量时间，是不值得的.

例3.(2010·全国卷Ⅰ理·12)已知双曲线E的中心为原点，P(3,0)是E的焦点，过P的直线l与E相交于A,B两点，且AB的中点为N(-12,-15),则E的方程式为

( )

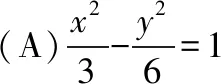
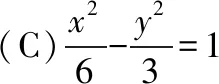
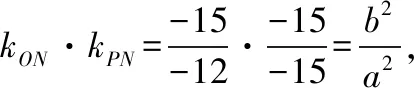
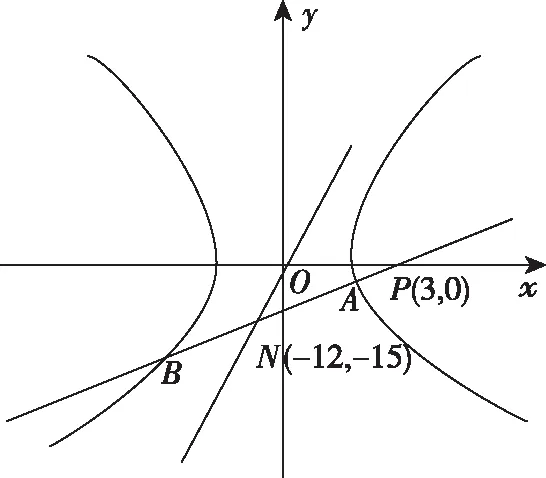
【评析】该题为2010年高考选择题的压轴题，利用已知结论就可秒杀考题，如此轻松就解决问题，大大地提升了解题效率，为解决其他问题节约了时间.

而2013年高考全国卷Ⅱ理科的21题也考查了椭圆中点弦公式，原题如下：

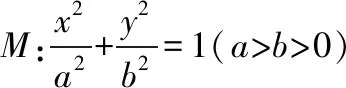
(Ⅰ)求M的方程;

(Ⅱ)C,D为M上的两点,若四边形ABCD的对角线CD⊥AB,求四边形ABCD面积的最大值.

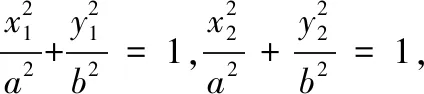
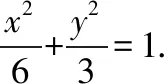
2015年全国卷Ⅱ文科更是直接考查了中点弦公式的证明，原题如下：

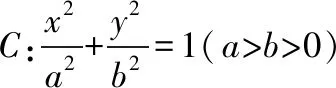
(I)求C的方程；

(II)直线l不经过原点O,且不平行于坐标轴,l与C有两个交点A,B，线段AB中点为M,

证明：直线OM的斜率与直线l的斜率乘积为定值.

这里我们就不再证明了，下面来看看抛物线.

1.2抛物线的几个重要结论及其直接应用

设直线l与抛物线y2=2px(p>0)交于A(x1,y1),B(x2,y2)两点，弦AB的中点为M(x0,y0)，则有以下结论：

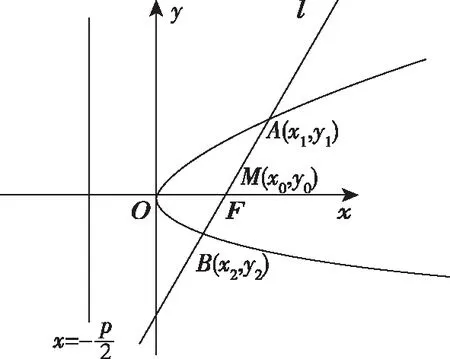
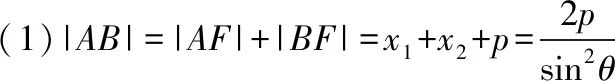
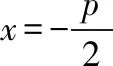
(5)以AF(或BF)为直径的圆与y轴相切；

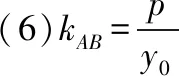
事实上推导以上结论的必经过程是：

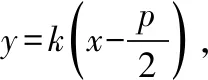
下面我们利用以上结论中的几个直接结论来快速解决高考试题.

( )

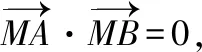
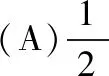
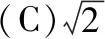
【分析】此题若采用一般方法处理，则需要设出直线方程并与抛物线方程联立，最后结合韦达定理进行求解，方法并不复杂，但是过程较多，计算量大.总体上看，其实就是用解答题的解题流程来解决选择题，这是很“不划算”的，而使用抛物线的相关结论直接解题，就可避免中间一系列的解题流程，找到快速解题的突破口，其实这里并没有技巧，只是我们记下了“结论”，省略了“推导过程”，这样就大大地提升了解题的效率.

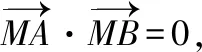
由图中的几何关系可知y0=2，再由结论(6)得：

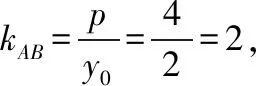
该解法使用了两个抛物线的结论就“秒杀”了该题，规避了大量的化简和计算，提升了解题的效率.

下面来看看2018年全国卷Ⅲ理科16题.

例7.(2018·全国卷Ⅲ理·16)已知点M(-1，1)和抛物线C:y2=4x，过C的焦点且斜率为k的直线与C交于A，B两点．若∠AMB=90°，则k=________.

此题竟然与例6惊人的相似，几乎是以原题的形式呈现出来，且处理方法一模一样，当然这也再次强调了研究高考题的价值和必要性.同样也说明了掌握现成结论解题能提升解题效率.其他结论的直接应用,读者可以在高考试题中发现，这里就不详细说明了.

2.高考试题是对教材例题、习题的再挖掘和再探索

高考试题源于教材、回归教材的同时又高于教材，如果我们对教材中的典型例题进行深入的挖掘和探索，就会找到很多高考试题源于对教材例题、习题的再开发和再利用.

下面我们来看看圆锥曲线中源于对教材例题的深入研究和探索得到的直接结论在解决高考试题上的直接应用.

源于人教版选修2—1第41 页的例题3：

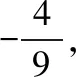
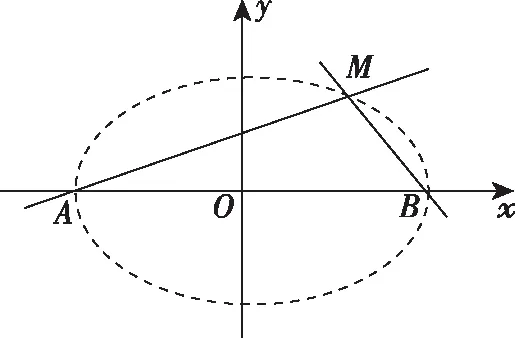
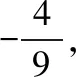
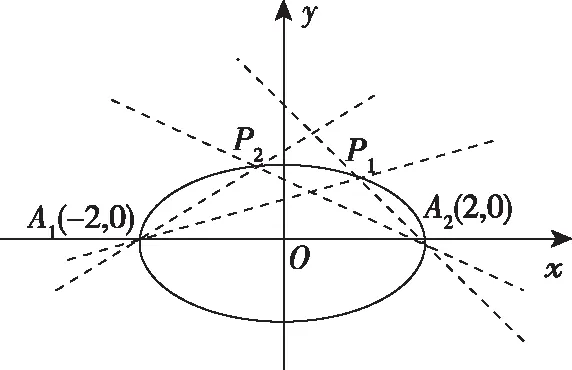
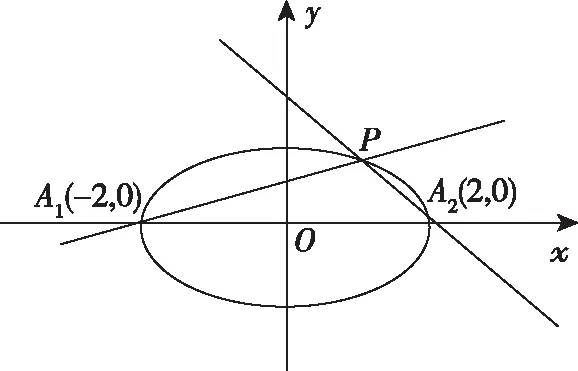
如果对该例题进行逆向思考和探究可以猜想：椭圆上异于左右顶点的动点与左右顶点的斜率乘积应该为一定值，定值为多少？经过推导和推广可以给出如下两个结论.

2.1已知A,B为椭圆：的左右顶点，点P为椭圆上异于A,B的动点，则有：

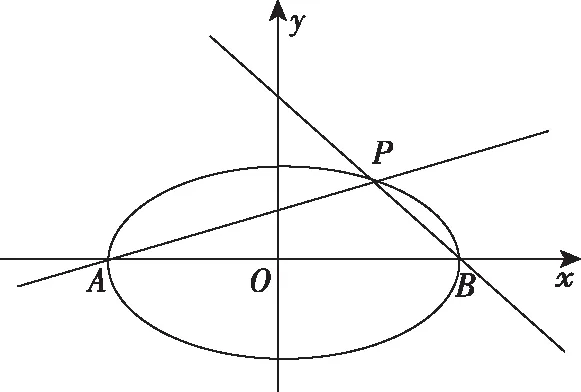
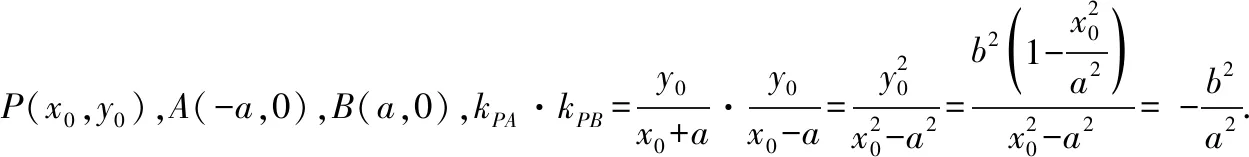
对于双曲线也有类似的结论.而教材也以探究的形式给出了其结论的一种形式.

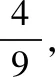
2.2已知A,B为双曲线的左右顶点，点P为双曲线上异于A,B的动点，则有：

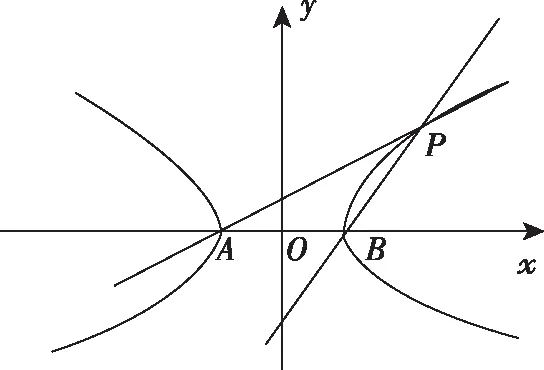
证明略.

事实上，以上两个推广的结论就是椭圆、双曲线的第三定义.而通过对以上两个结论与椭圆、双曲线的中点弦公式进行比对发现，结果的定值结构是一致的，故可在学习时一并记住，而记住了这些结论就可以快速地解决一些使用常规方法比较复杂的题型，从而在解法上给试题“瘦身”，大大提升了解题效率.

( )

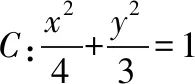
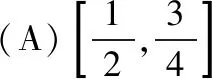
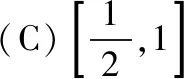
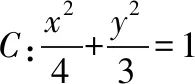
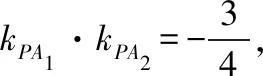
【点评】常规解法较容易想到和执行，但其计算量较大，对于一个选择题而言，用解决大题的方法和时间去处理是不太合理的，如果掌握了相关结论就可省去许多复杂的计算，直接利用结论来快速解题，这样既节省了时间又提高了解题的正确率，何乐而不为！

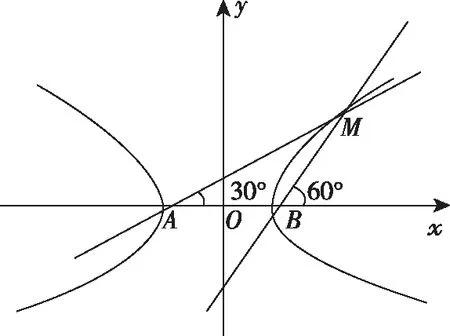
例10.(2015·全国卷Ⅱ理·11)已知A，B为双曲线E的左、右顶点，点M在E上，△ABM为等腰三角形，且顶角为120°，则E的离心率为

( )

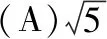
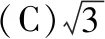
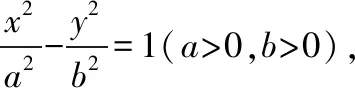
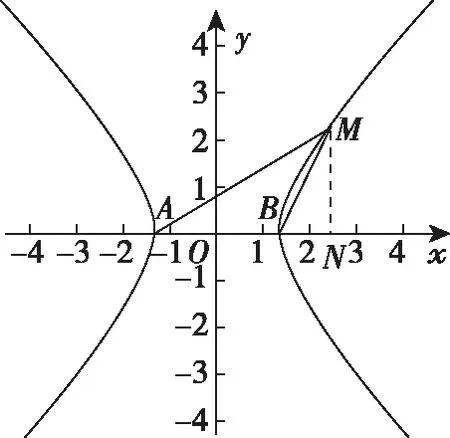
【快速解法】如图，据已知条件可知∠MAB=30°,∠MBx=60°，故有：

这里要提醒读者，利用现成结论快速解决高考试题时需要记清、搞懂现成结论的前提条件，如果忽略条件而一味只记住结论直接应用往往就会得不偿失.当然，利用一些结论直接解题一方面提高了解题效率，但另一方面值得注意的是，不是所有的问题都可以直接用现成结论或技巧去解，掌握解决问题的通法才是拿下数学高分的利器，近年来高考试题的命题规律和方法已充分说明了这一点.高考试题强调解决问题的通性通法，淡化技巧，如果广大考生能够在掌握好这一原则的同时，在适合的题目、题型的背景下利用现成结论秒杀考题，就会锦上添花！

3.深入挖掘教材中的例题、习题的几点思考

(1)要善于从课本的例题、习题中归纳总结出解决问题的基本思想、基本方法，做法是：可以将近几年高考试题中利用通性、通法解决的问题汇编成题组(该项工作由教师完成)，再利用练习课的时间进行限时训练，及时进行讲评.讲评过程中建议将高考题涉及的课本原型题进行对比分析，并归纳总结出解决问题的思想、方法，这样学生更能感受到教材的重要性；

(2)重视对教材典型例题、习题的深层分析，并在可能的情况下根据高考试题的命题特点和考点将例题、习题进行延伸、推广和拓展，这些深入挖掘得出的结果将会帮助学生快速解决问题.当然这就需要教师把课本的典型例题、习题讲透、适当加深，最终使学生在高考考场上左右逢源；

(3)需要注意的是，不是课本上的每一个例题、习题都需要去挖掘和深究的，结合高考的命题特点和走向以及在《课程标准》、《考试大纲》的指导下有目的的对教材进行“再开发”、“再利用”才是重点.学生听到了老师“回归教材”的建议，就想当然地觉得通读一遍教材即可，这就大错特错了，只有带着对高考试题的认识回归课本、深究知识，才能真正抓住高考试题所考查问题的本质，在从容应对高考试题变化的同时提升对教材的理解.

4.对高考复习备考的建议

(1)教学中要认识到“回归课本、回归本质”的重要性，高考试题其实就是对课本知识的再重复和再升华，最后还是要回归到知识的本质上来.所以复习时脱离教材，过分依赖教辅材料，不花时间和力气去研究教材就会导致学生对课本中的概念、基本思想方法模糊不清，对解决问题的通性、通法不熟练，最终导致高考中的失利.

(2)用好高考试题，毋庸置疑，无论对于教学还是考试，高考试题具有较强的指导意义.高考试题源于教材、又回归教材，同时遵循“立足基础，考查能力”这一重要原则，其宗旨是：测试中学数学基础知识、运算能力、空间想象能力以及分析运用知识解决实际问题的能力，不管高考命题如何改变，我们都能在每一份高考试题中找到大量的教材原题或由这些原题进行引申、变化而来的试题，甚至可以用挖掘而来的结论直接、快速地解决高考试题.因此，我们应当用好高考题，带着它提出的问题回归课本，挖掘课本例题、习题的潜在价值，重视通性通法的同时提升解题效率.