随机振动下偏心隔振系统仿真分析

杨 强，董万元，邵 闯

（中国飞机强度研究所 结构冲击动力学航空科技重点实验室, 西安710065）

航空装备研制生产、训练使用、作战保障过程中长期存在的随机振动问题是国防科技领域研究的重点。现代飞机的超音速巡航、高机动、高隐身等要求使得其振动环境日益严酷，统计数据表明：飞机所发生的重大事故中，有40%与振动有关[1]。据美国军方的统计，振动导致航空电子设备失效的因素约占27%[2]。为了保证各类机载设备在复杂振动环境下正常工作，最经济可靠的方法是加装隔振器。

现代飞机装有大量机载设备，空间资源十分有限，导致部分机载设备的安装中心无法与设备重心重合，这增加了设备隔振安装设计的难度。仿真分析方法被引用到偏心设备前期隔振设计中，可明显节约设计成本，降低产品开发周期。彭超[3]、杨文芳[4]通过有限元法分析了机载设备的振动特性，根据分析结果设计减振系统。姜伟伟[5]采用Bushing 单元模拟了减振系统中的减振器，分析了光电成像设备减振系统在正弦扫频激励下的隔振参数，并用实验验证了仿真分析结果的精度。夏张辉[6]研究发现车下设备偏心会使设备的6个自由度振动发生耦合现象，导致各阶刚体振型及振型频率产生较大变化，致使车下设备固有频率偏离了原始设计最优值，减振效果降低、车辆运行平稳性变差。李晓波[7]通过有限元法研究了安装中心与弹性中心不重合所导致的线振动和角振动耦合。章博[8]通过有限元分析法调整减振器刚度，可以实现惯性测量系统的振动解耦。

针对某安装中心与结构重心不重合的机载设备，首先对偏心载荷解耦，计算各支撑点的载荷，依此设计偏心设备的隔振系统；建立隔振系统有限元模型，采用基础激励法分析隔振系统的加速度响应并与试验结果作对比，通过优化隔振系统的刚度和阻尼参数，获得较精确的动力学分析模型，为随机振动环境下偏心机载设备的隔振安装设计提供分析方法。

1 隔振原理

1.1 机载设备

某机载设备是控制发动机启停的重要设备，重量M=2.02 kg，外形尺寸为190 mm×120 mm×90 mm。以安装面中点为原点O，长度方向为X 轴，宽度方向为Y 轴，Z 轴由右手定则确定，建立O-XYZ 坐标系，设备重心坐标为(10,-33,-5)，安装点坐标分别为1#(0, 55, 0)、2#(0,-55, 0)、3#(90, 17, 0)和4#(90,-17,0)，安装中心与设备重心存在严重的偏心。设备在O-XYZ 坐标系下绕坐标轴的转动惯量为Ixx=3.460×10-3kg·m2，Ixy=-12.698×10-3kg·m2，Ixz=-0.453×10-3kg·m2，Iyy=4.897×10-3kg·m2，Iyz=0.383×10-3kg·m2，Izz=6.563×10-3kg·m2。

1.2 振动环境

机载设备振动谱是在宽带随机谱上叠加4个窄带尖峰，如图1所示。

图1 随机振动谱

窄带的基频为F1=178.5 Hz，其余3 个频率分别为F2＝2F1、F3＝3F1、F4＝4F1，每个谐振频率带宽等于对应中心频率的±5 %，每个频率对应的峰值为1.6 g2/Hz。

1.3 隔振原理

隔振主要作用是减小设备和振源之间的动态耦合，减少不良振动传递到设备中。典型的隔振系统是假设被隔振物体为刚体，基础为刚性，隔振器简化为弹簧K 和阻尼器C 的无质量部件，其力学模型见图2。

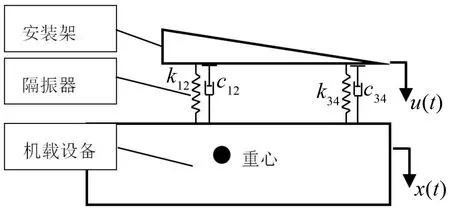
图2 隔振系统示意图

则该系统用动力学方程表示

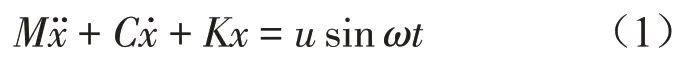
隔振系统的传递系数T为[9]

其中：M为设备质量；C隔振系统的阻尼；K为隔振系统的刚度；

当f=fn时，传递系数T 称为隔振系统的放大倍数Q。

2 隔振系统设计

航空机载设备内部结构复杂，集成度高，零部件众多，较难保证设备重心在几何中心，又因机上安装空间及方式受限，常常导致安装中心与结构重心无法重合。因此，本文以某偏心机载设备垂向为例，设计了一套隔振系统。

2.1 偏心质量计算

偏心系统设计首先要精确计算各支撑点承受的质量载荷。机载设备的4 个安装点已经给定，且为垂向吊挂形式，因此，垂向的质量计算是隔振设计首要考虑的因素，先计算每个安装点的垂向质量。因3#和4#点距离很近，设为一个安装点，那么，系统在垂直方向就可以看作3 点支撑，则各点在垂直方向的质量计算公式[1]为

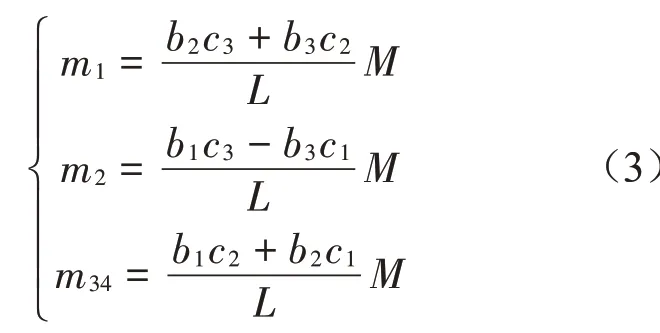
其中：L=b1c2+b1c3+b2c1+b2c3+b3c2-b3c1；

bi、ci(i=1,2,3)分别是i#隔振器在X 轴和Y 轴方向与重心的距离。

通过计算可得3 点垂直方向的质量分别为m1=0.707 kg，m2=1.089 kg，m34=0.224 kg。

由于3点质量不同，且差别较大，需设计不同载荷的隔振器，且要保证各点变位相同，隔振器刚度设计应满足

得到

即k1=0.65k2，k34=0.206k2。

2.2 固有频率计算

由图1 知机载设备振动谱有4 个高量值的窄带尖峰，隔振系统的固有频率需要避开此频率。由隔振理论可知，系统的固有频率应小于126.22 Hz。由式（2）传递系数计算系统不同固有频率和放大倍数Q下的隔振效率，见表1。

由此可以初步确定隔振系统设计选择工况5，即固有频率为90 Hz，放大倍数Q 为3，则阻尼比ξ 为0.15，此时系统的隔振效率为56.59%。

2.3 刚度计算

由工况5可以计算隔振系统固有频率总刚度为645.95 N/mm，隔振器的刚度分别为k1=226.08 N/mm，k2=348.24 N/mm，k34=71.63 N/mm。

2.4 阻尼计算

由式（2）中阻尼比ξ公式可以计算各隔振器的阻尼分别为c1=139.93 N/(m/s)，c2=15.54 N/(m/s)，c34=44.33 N/(m/s)。

3 有限元建模及分析

随机振动响应分析采用基础运动法[10]施加激励，采用模态叠加法计算振动响应。

3.1 有限元模型

安装架是长和宽为250 mm×140 mm、厚度为2 mm的薄板，中间带一条加强筋，长和宽都远大于厚度尺寸，因此采用三维壳模型，选择S4R 壳单元，单元长度为1，共划分29 024 个单元。安装架材料为30 CrMnSiA，经过热处理，弹性模量为210 GPa，抗拉强度为1 180 MPa，σ0.2为835 MPa，泊松比为0.33，密度为7.75 g/cm3。机载设备在隔振系统中只是一个辅助质量件，采用解析刚体分析，采用R3D4 单元，共划分26 227 个单元，刚体参考点RP 设在设备的重心上，设备的重量和惯性矩等载荷施加在参考点RP上。

将隔振器简化为线性弹簧阻尼单元，采用Springs/Dashpots 单元模拟，单元底部通过Coupling中Kinematic 方式与设备RP 参考点连接，单元顶部采用相同方式与安装架的隔振器安装孔连接，建立机载设备隔振系统的有限元模型，如图3所示。

图3 有限元模型

根据隔振器性能参数计算Springs/Dashpots 单元的刚度和阻尼矩阵。为了便于表述，将安装架6个连接孔编号为1#至6#，安装架与34#隔振器连接的边缘孔编号为7#。

隔振系统有限元计算的载荷谱是1.2 小节给定的振动环境谱，采用基础运动法施加到隔振系统中。

隔振系统的边界条件为1#至6#连接孔固支。

3.2 分析方法

进行随机振动响应分析时先做模态分析，计算固有频率和振型，获得大于最高激励频率2 000 Hz的固有频率。经预分析，得到第13、14 阶固有频率分别为1 860.8 Hz 和2 306 Hz，因此在Random response分析中选取1至14阶模态，分析频率范围为15 Hz～2 000 Hz，每阶模态设置45 个分析点，偏置系数为3；每个分析步输出设备参考点RP 的加速度响应结果。对于隔振系统，前6 阶模态与隔振器有关，第7阶之后的模态与安装架结构有关，安装架为30CrMnSiA材料，其自身的阻尼较小，因此设置第7阶至第14 阶模态阻尼比为0.025，对应品质因数为20。随机振动分析采用基础运动法，运用Acceleration base motion 法将激励载荷谱施加到隔振系统约束边界上，即1#至6#点对应的载荷方向。

表1 不同固有频率和放大倍数计算表

3.3 随机振动响应分析与优化

经过初步随机振动分析，得到隔振系统中机载设备的振动加速度响应，见表2中优化前类别，机载设备加速度响应功率谱密度曲线如图4中计算曲线所示。将初步分析结果与试验数据对比发现，X 向加速度响应误差为26.14 %，固有频率误差为33.34%；Y 向加速度响应误差为44.95%，固有频率误差为37.43%；Z 向加速度响应误差为62.72%，固有频率误差为-44.44%。系统的响应、固有频率、放大倍数和隔振效率等参数的计算结果误差都很大，为此，依据试验结果继续优化有限元模型。

对于隔振系统，影响隔振参数的主要因素是隔振器的刚度和阻尼。因此，以1# 、2#和34#隔振器的刚度和阻尼为优化参数，以隔振系统加速度响应和固有频率为优化目标，优化隔振系统的Y向，然后计算其他方向结果。优化结果如表2中优化类别所示，加速度响应功率谱密度曲线如图4 中优化曲线所示。

4 结果对比与分析

4.1 结果对比

将隔振系统通过夹具固定到在电磁振动台上，按照图1给定的随机振动试验谱，采用GJB150.16A-2009 规定的试验方法，分别完成隔振系统3 轴向的振动试验测试，测得机载设备加速度响应曲线如图4所示，试验结果如表2所示。

4.2 分析与讨论

由表2中隔振系统仿真优化与试验结果对比可知，优化后隔振系统各参数仿真计算的精度均有较大程度提高。优化后Y 向的振动响应误差从44.95 %降到7.47 %，固有频率的误差从37.43 %降到-0.25 %；X 向的振动响应误差从26.14 %降到3.82%，固有频率的误差从33.34%降到7.79%；Z向的振动响应误差从62.72%降到37.16%，固有频率的误差从-44.44%降到15.87%。

由图4(a)和图4(b)可以看出，优化后的X 向和Y向功率谱密度响应曲线与试验测试曲线在1阶固有频率处吻合较好，而图4(c)中Z向优化和试验均有两个响应峰值，优化的第2阶频率为117.81 Hz，对应放大倍数为3.717，而试验的第2阶频率为230.0 Hz，对应放大倍数为2.023，仿真结果比试验值都偏低了，这是由于机载设备重心在Z 向偏心最严重，导致设备在Z向振动中激起绕X轴摆动模态。

图4 随机激励下机载设备加速度响应曲线

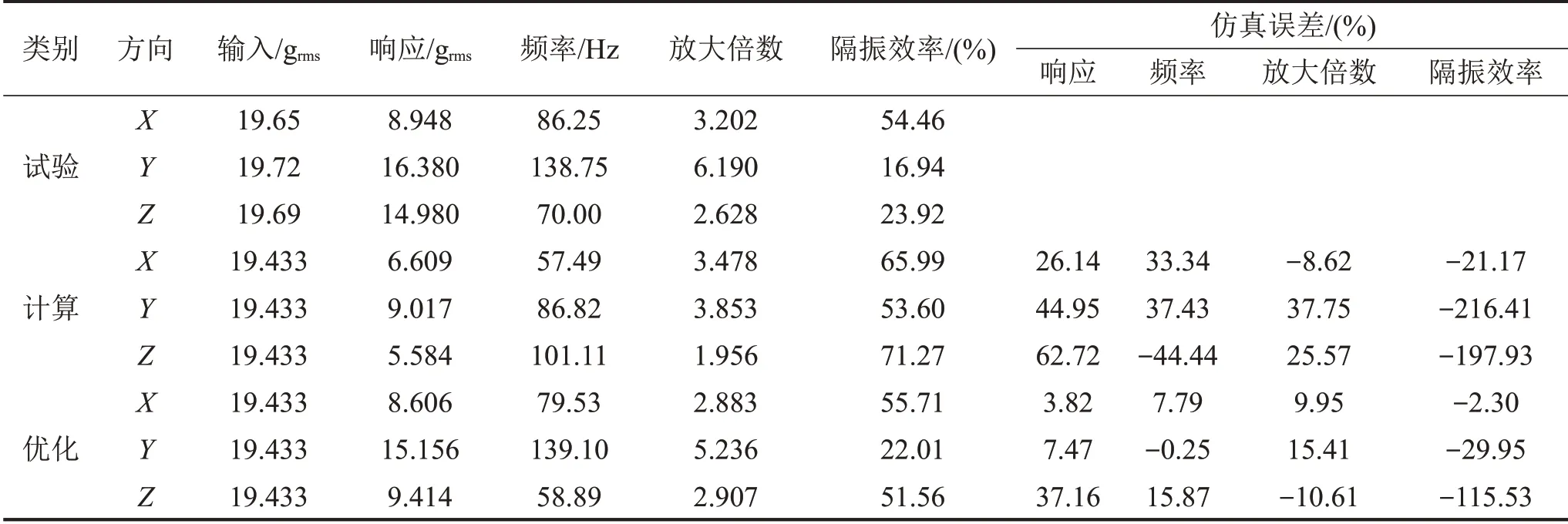
表2 机载设备随机振动仿真与试验对比表

由表2 中隔振系统优化与试验结果对比可知，优化后的放大倍数与试验测试结果误差最大的是Y向，最大误差为15.41%，其余两轴向的误差也都在10%左右，这是因为在仿真计算时很难将隔振器的阻尼预计准确，本文所用隔振器为金属丝网类，其阻尼比ξ一般在0.1～0.2之间，优化后ξ=0.175。

由图4中隔振系统优化和试验功率谱密度曲线对比可以发现，功率谱密度曲线在中低频段内与试验响应吻合较好，而在较高频段内，仿真分析的响应曲线均低于试验结果。这是由于仿真时将隔振器简化为线性弹簧阻尼单元，而弹簧系数和阻尼系数只能按照隔振器刚度曲线拟合得到，未能考虑隔振器内部弹性元件因高频振动而产生的驻波效应对隔振系统的影响。因此，也导致了仿真分析时隔振系统的隔振效率都优于试验测试的结果。

5 结语

在飞机中，常存在机载设备安装中心与重心偏离较大的情况，给设备的隔振安装设计带来很大难题。本文针对某偏心机载设备，设计了一套隔振系统，并建立隔振系统有限元分析模型。通过加速度响应动力学仿真分析，证明本文设计的隔振系统可以满足偏心机载设备的隔振要求；通过优化分析，得到隔振系统较精确动力学模型，为随机载荷环境下偏心机载设备的隔振安装提供分析方法。