基于Euler Bernoulli理论的压电系统集中参数模型修正

宋伟志，周 辉，张晨骏，陈智勇，赵海军，2，岳遂录

（1.洛阳理工学院，河南 洛阳471023； 2.天津职业技术师范大学，天津300222）

近些年，微电子机械系统（MEMS,Micro-Electro-Mechanical System）及集成电路超低功耗技术（Ultra-low power integrated circuit technology）得到快速发展，无线电子设备的功耗降到了微瓦数量级，这使得利用振动能量收集器为这些设备提供电能变为可能。压电俘能系统由于结构简单、抗电磁干扰能力强而得到国内外学者的广泛研究[1–7]。常用的俘能系统设计是基于悬臂梁结构，如图1所示。

在系统建模分析中，多采用集中参数模型[2–4,8–10]，如图2所示。这种模型以集中参数描述悬臂梁的运动机理（一般描述自由端运动）。这些参数包括等效刚度keq、等效质量meq、等效阻尼ceq。keq可以通过在悬臂梁自由端施加集中荷载，测量其静态形变量来求得，meq可以在基础静止情况下，借助瑞利商数[11]将悬臂梁的动能表示为自由端速度形式获得，ceq可通过振子半衰期或阻尼振动曲线来求得。

图1 基础平动及转动时悬臂梁示意图

然而，压电俘能系统悬臂梁结构振动属于基础激励问题，悬臂梁振动由本身惯性激励引起，在悬臂梁质量不可忽略的情况下，悬臂梁分布质量对激励项贡献一惯性力，而当M/meq≤1（M为悬臂梁末端质量，meq表示悬臂梁质量）时，上述惯性力对激励幅值影响显著，此时使用集中参数模型会产生较大误差。

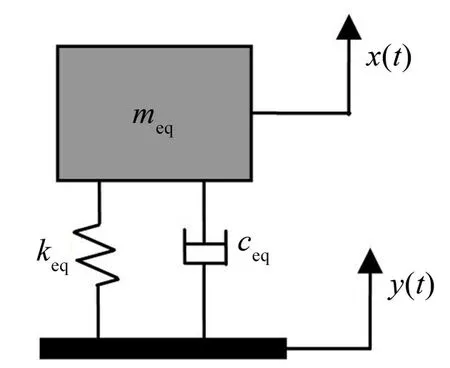
图2 悬臂梁基础激励下集中参数模型

针对上述存在问题，本文基于Euler Bernoulli理论，分别分析了Euler Bernoulli模型和集中参数模型自由端位移响应，利用悬臂梁末端相对位移传递函数，研究了在一阶模态下集中参数模型峰值传递率的误差，在理论推导的基础上，对集中参数模型进行了修正，仿真及有限元分析表明，在1 阶模态附近，修正后的集中参数模型峰值传递率误差大幅降低。

1 集中参数模型修正分析

1.1 简谐激励下集中参数模型运动学分析

如图2 所示，为便于分析，以y(t)表示基础位移、x(t)表示等效质量meq位移响应建立系统运动学方程，如式（1）所示。

在简谐激励下，基础激励表示为：y(t)=Y0ejωt，设meq位移响应为：x(t)=X0ejωt，可分别求得

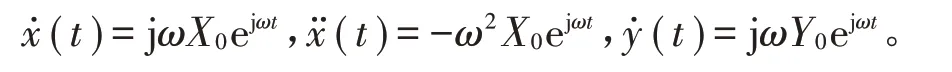
将上式分别代入方程式（1）可求得

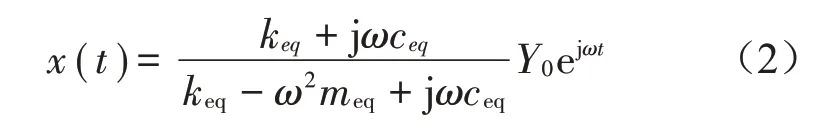
鉴于压电系统工作过程中，工作效率取决于等效质量与基础间的相对运动，故引入等效质量与基础相对运动z(t)，易知

将式（2）代入式（3）可得

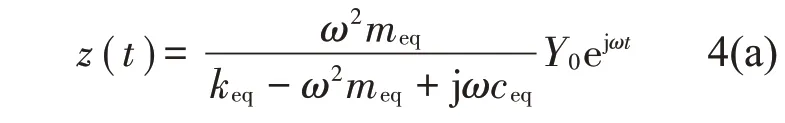
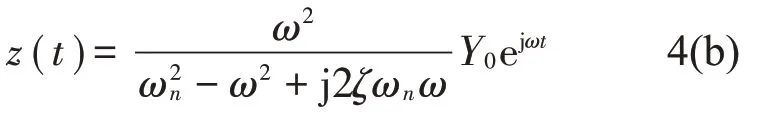
1.2 简谐激励下Euler Bernoulli模型运动学分析

对于图1 所示悬臂梁结构，以g(t)表示悬臂梁横向运动，h(t)表示悬臂梁小幅转动，以w(x,t)表示悬臂梁上任一点横向位移，则悬臂梁振动方程为

式中：E 表示悬臂梁弹性模量，I 为悬臂梁截面关于中性轴惯性矩，m 表示悬臂梁单位长度下的质量，cs为悬臂梁应变率阻尼系数，在机电复合结构下通常表示为csI，ca为空气阻尼系数。

同上，为分析悬臂梁末端与基础间相对运动，引入wb(x,t)、wr(x,t)。其中wb(x,t)表示基础位移，wr(x,t)表示悬臂梁末端相对于基础位移，则

将式（6）代入式（5）可得到

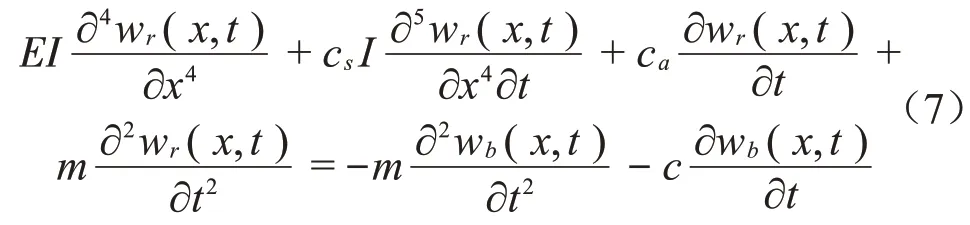
即为悬臂梁末端相对位移的运动方程。由式（7）可知，悬臂梁激励包括惯性力及外部阻尼效应。

方程式（7）的解可表示为收敛本征函数级数的形式[12]

对于悬臂梁结构，相对运动的边界条件为

在比例阻尼情况下，质量归一化本征函数φr(x)同样适用于无阻尼自由振动，则边界条件可简化为

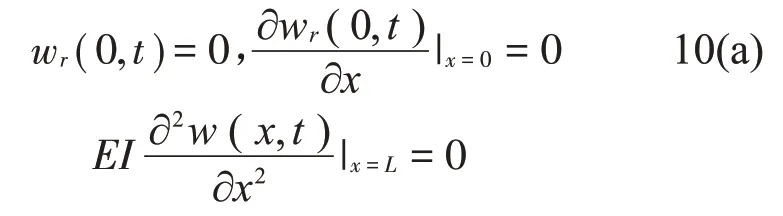
由上述公式及边界条件可得第r 阶模态下质量归一化本征函数

其中：λr为r 阶模态下的无量纲频率，由特征方程式（12）求得。

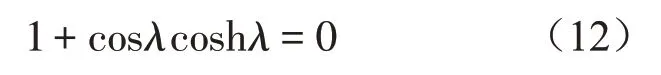
参数σr如式（13）所示

以δrs表示克罗内克尔符号表示第r 阶模态的固有频率，则式（11）满足以下正交条件[12]

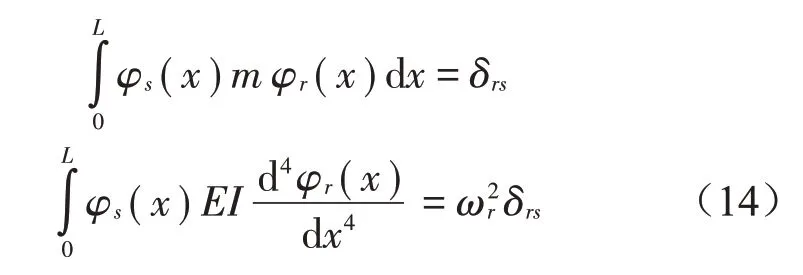
结合式(7)、式(9)、式(14)，可将偏微分方程转化为无限常微分方程集合[13]

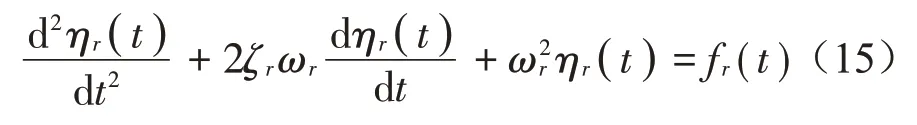
其中：ζr为系统阻尼比，fr(t)为模态力函数，可具体表示为

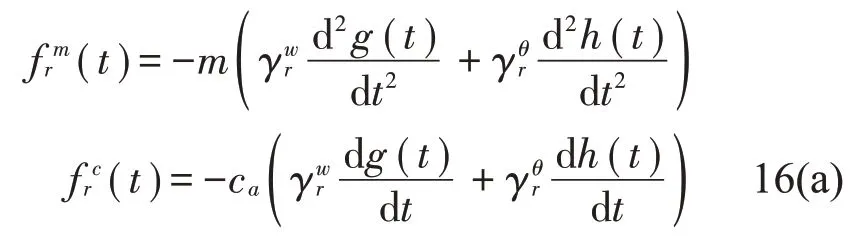
其中：

在初始条件为0时，求得模态力函数情况下，利用杜哈梅积分可求得模态响应：

综上，结合式（11）、式（17），可求得式8(a)中悬臂梁任何部分的振动响应

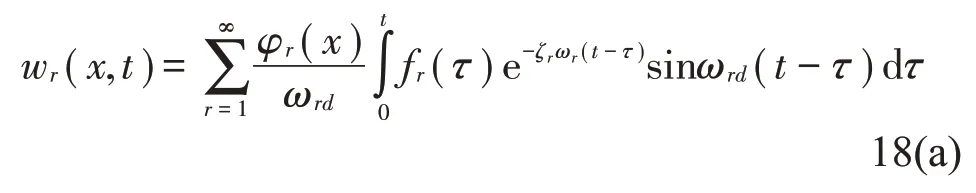
在压电俘能系统研究中，悬臂梁运动一般采用简谐平动来化简问题，基础平动如式18(b)所示，且基础不会发生转动，故h(t)=0。

式中：A0为基础简谐振动的振幅，ω为激振频率，j为虚数单位。

将式18(b)代入式（17）可求得简谐激振下的模态响应

由式18(b)、式（11）、式18(b)、式（19）可求得在简谐激励下悬臂梁自由端（x=L）的振动响应，如式（20）所示

1.3 Euler Bernoulli及集中参数模型对比分析

利用上一小节推理结论，分析对比Euler Bernoulli及集中参数模型在简谐激励下的相对位移传递率，相对位移传递率定义为悬臂梁自由端相对位移响应与基础位移输入间的比值，同时对方程进行无量纲化，引入频率比Ω =ω/ωr，则可分别得到两种模型下的相对位移传递率

根据两模型传递率函数，对系统1 阶模态（r=1）进行分析，式中λ1、σ1可通过式（12）、式（13）确定。同时，由于传递率公式为阻尼比的函数，所以有必要对两模型在不同阻尼比时的传递率函数进行分析，分析结果见图3。

由图3易知，在阻尼比相同情况下，集中参数模型传递率峰值存在较大误差，阻尼比较小情况下，1阶固有频率附近其误差达到36.14%。此外，由于集中参数模型为单自由度模型，不能反映悬臂梁高阶模态，故随着频率比的增大，其误差会进一步加大。

2 悬臂梁集中参数模型修正

当悬臂梁在低频附近受到激励时，由Euler Bernoulli 模型推出的相对位移传递率函数，可只取求和中的首项，而对于r ≥2 的项可忽略不计，则Euler Bernoulli模型中相对位移传递率函数为

图3 阻尼比不同时两模型传递率比较

引入传递率幅值修正参数α1，式（22）可简化为

其中：

结合式（12）、式（13）、式（23）可求得修正参数值α1≅1.565 98。即：如果集中参数模型固有频率足够精确，集中参数模型乘以修正因子α1即可得到Euler Bernoulli模型在低模态的简化解。

为对上述修正因子的正确性进行验证，分别做出集中参数模型、集中参数修正模型以及Euler Bernoulli 模型在阻尼比为ζ=0.05 时的相对运动传递率曲线进行对比，结果如图4所示。

由图4可知，修正后的集中参数模型在1阶模态附近较大的频率比范围内和Euler Bernoulli 模型吻合很好，在1阶模态之前，其相对位移传递误差不超过5%，在2阶模态附近开始有所偏差。但根据未修正的集中参数模型所求得的相对运动幅值存在很大偏差。

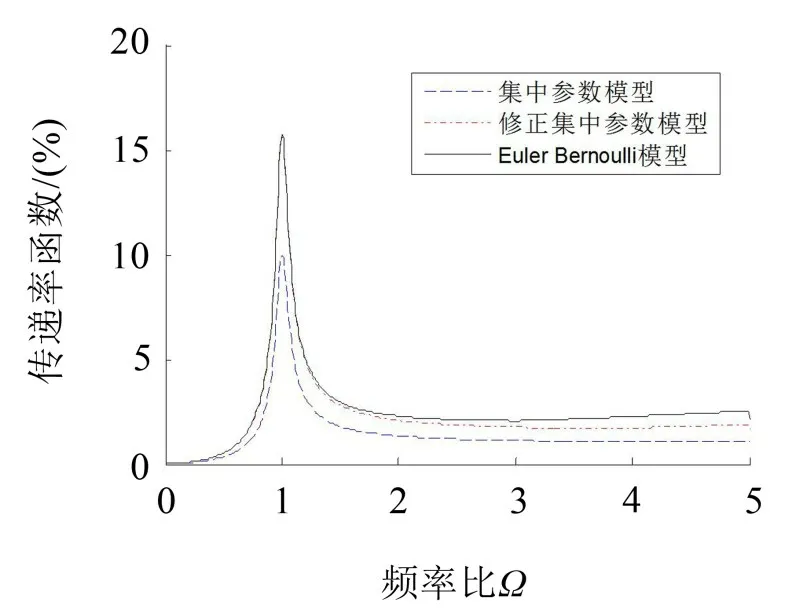
图4 集中参数、修正集中参数及Euler Bernoulli模型相对位移传递率函数曲线（ζ=0.05）

对上述修正后的集中参数模型进行验证，利用HyperMesh 建立了悬臂梁的有限元模型，有限元分析中，模型选用的参数及边界条件如下。

表1 （a）模型信息

表1 （b）材料信息

边界条件：

扫频范围：1 Hz～81 Hz；

阻尼比：0.05；

载荷：约束点施加竖直方向的强制位移，为便于分析，位置幅值为定值1 mm。

分析中悬臂梁约束端及自由端振幅、位移传递率结果见图5。

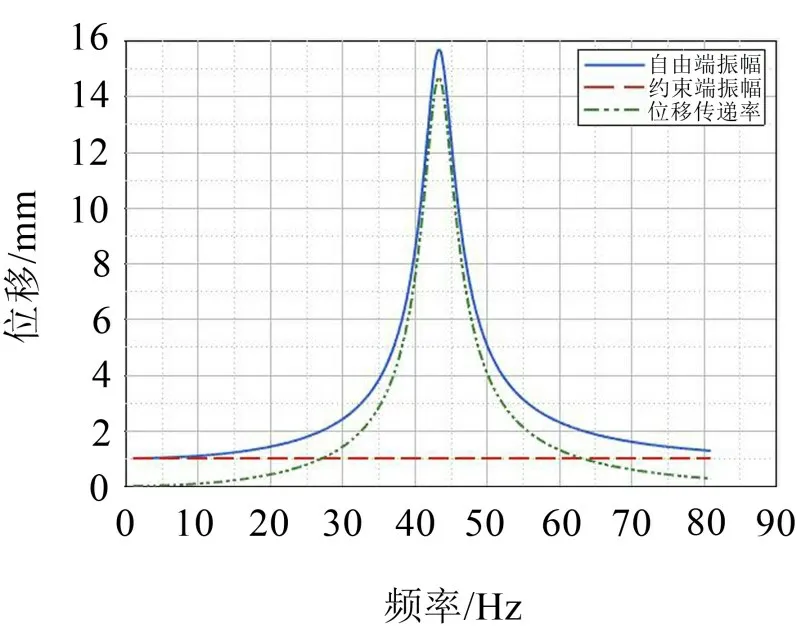
图5 悬臂梁约束端及自由端位移、位移传递率

为便于表示系统1 阶模态附近的响应特性，做出悬臂梁系统在频率比下的位移传递率曲线，如图6所示。

分析系统在1 阶模态处位移传递率误差，结果见表2。

表2 1阶模态处悬臂梁位移传递率误差

图6 悬臂梁位移传递率

由上述结果可知，修正后的集中参数模型与有限元分析结果较为吻合，其在1 阶模态处位移传递率误差为4.71%，而未修正的集中参数模型误差达到32.75%。综上可得，利用修正后的集中参数模型在低频阶段分析运动响应特性更为准确。

3 结语

为提高悬臂梁压电系统集中参数模型的预测性能，利用Euler Bernoulli模型对集中参数模型进行了修正。通过模型结果对比及数值分析得到：未修正的模型相对位移传递率存在较大误差，其误差值一度达到32.75%，而修正后的集中参数模型相对运动幅值传递率曲线在1 阶模态附近与Euler Bernoulli模型吻合很好，其误差不超过5%，只有在2 阶模态以后开始出现偏差。这说明提出的修正模型在低频工作频段具有较好的预测性能。利用上述结论，在简化悬臂梁模型的基础上，可进一步提高分析模型运动特性的准确性，这对悬臂梁结构在工程应用中的建模分析具有一定价值，尤其在悬臂梁式压电俘能系统建模分析中，可更加准确地对系统输出功率进行预测及处理。