逆压电条件下压电悬臂梁可靠性计算
方永锋,程正伟,张卫华
(贵州工程应用技术学院机械工程学院,贵州毕节 551700)
0 引言
压电智能结构由于其自身特有的正压电与逆压电效应,在航空航天、汽车、建筑等领域得到广泛的应用,关于压电材料的正压电效应研究成果比较多[1-3]。文献[4-6]研究了正压电效应下的压电结构的应用,给出了不同场合、不同工况下的压电结构的应用原理与方法。相对来说,关于逆压电条件下的结构分析研究起步较晚,成果较少,文献[7]研究了空间桁架结构自适应控制,发现压电结构在逆压电条件下,可以使空间桁架结构达到自我控制、自我适应的效果。文献[8]研究了压电驱动装的输入域输出,为月面巡视器提供了技术基础。关于逆压电条件下的结构可靠性研究的成果较少,文献[9-10]研究了结构与系统的可靠性,给出了大数据条件下与区间条件下的结构与系统可靠性的计算方法。文献[11-12]研究了压电桁架结构在电载荷和机械载荷联合作用下的可靠性分析,给出了压电桁架结构的失效路径,表明在逆压电状态下,可以明显的提高结构的可靠度。文献[13]研究了压电陶瓷执行器的力学行为,给出了其力学行为的计算模型,说明研究压电陶瓷的力学可靠度对于工程实践很有意义。
本文通过对逆压电条件下的压电悬臂梁的力学可靠性与电学可靠性进行研究,给出压电悬臂梁在逆压电状态下的可靠度的计算方法。在此基础上,对计算模型做进一步的简化,用一个工程算例说明本文方法的优点。
1 逆压电条件下压电悬臂梁抗力与电场强度分析
根据压电悬臂梁服役条件、服役环境等条件与相关文献[1-3],本文采用压电材料第二边界条件的压电本构方程,即机械加持,电路短路边界条件的压电本构方程为:
σ=cEε-eEE
(1)
D=eε+ΞE
(2)
式中:σ为应力向量;cE为短路弹性刚度系数矩阵;eE为短路压电应力常数矩阵;ε为应变向量;e为压电应力常数矩阵;E为电场强度向量;D为电位移向量;Ξ为极化后的夹持介电常数矩阵。
一般来说,压电悬臂梁结构为中间是矩形铁芯,上下两层从内到外依次粘上PZT,采用电学串联与力学叠加的方式,如图1所示。
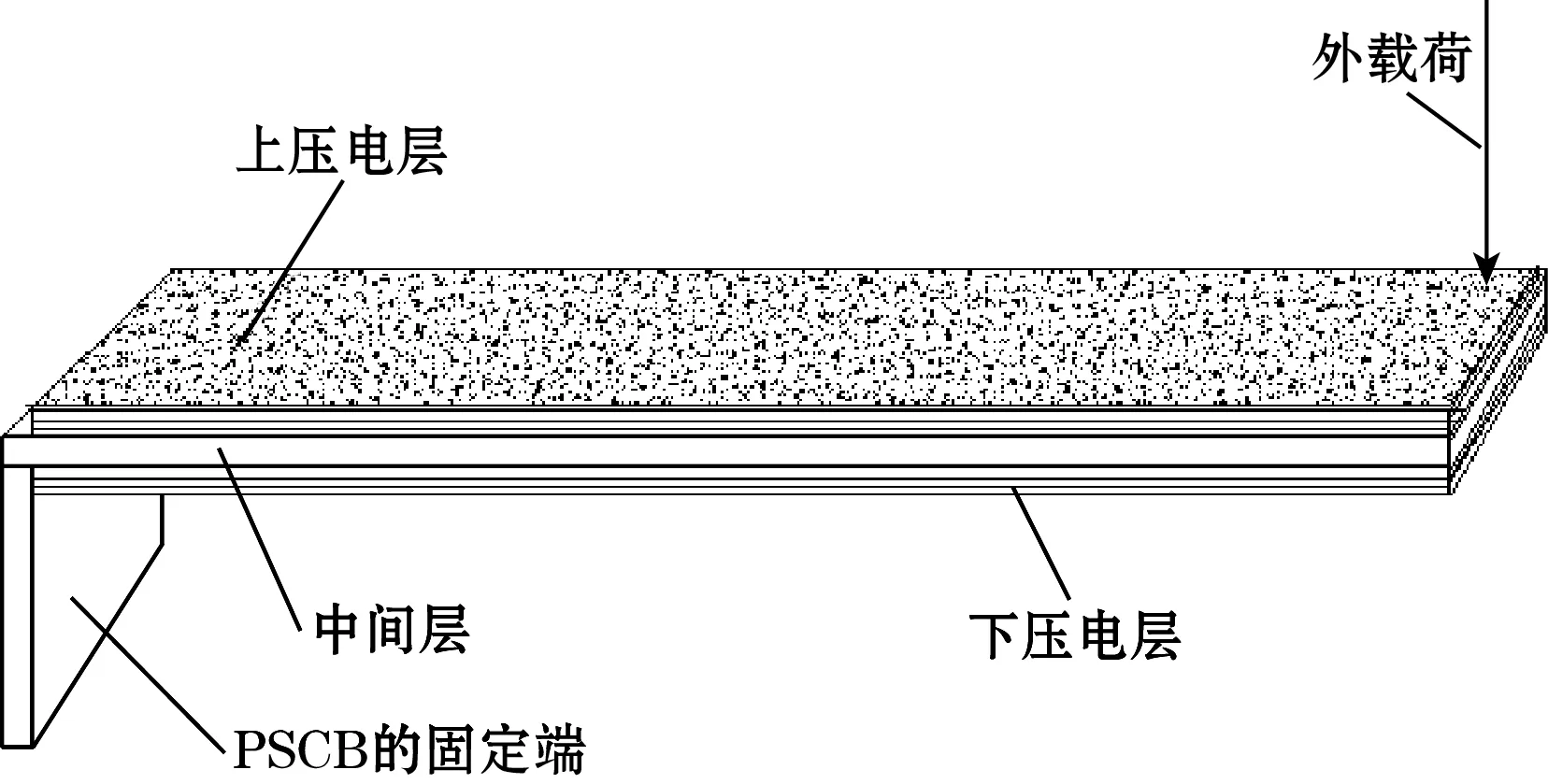
图1 压电悬臂梁
对于双面粘有压电材料的压电悬臂梁,考虑其沿轴向伸长与缩短,则由式(1)、式(2)可得:
(3)
(4)
(5)
(6)
式中:Nu、Nd分别为压电悬臂梁上、下压电层产生的抗力;c11为cE在轴向的弹性模量;Au为压电悬臂梁上压电薄片压电层的截面积;Lu为压电悬臂梁上压电层的长度;Δuu为悬臂梁上压电层的轴向变形量;e33为e的垂直于轴向的压电应力常数;hu为悬臂梁上压电薄片的厚度;ΔEu为悬臂梁上压电薄片的电势差;Ad为压电悬臂梁下压电层的截面积;Ld为压电悬臂梁下压电层的长度;Δud为压电悬臂梁下压电层的轴向变形量;hd为悬臂梁下压电薄片的厚度;ΔEd为悬臂梁下压电薄片的电势差;Qu、Qd分别为压电悬臂梁上、下压电层的电荷量;nu为压电悬臂梁上压电薄片层数;Ξ33为Ξ的垂直于轴向的压电夹持常数;nd为压电悬臂梁下压电薄片层数。
2 逆压电条件下压电悬臂梁可靠度计算
逆压电悬臂梁对于普通悬臂梁来说,具有智能化的微调作用,当悬臂梁的挠度超过一定范围时,压电层就会收到反馈,利用逆压电效应对悬臂梁的进行修正,使得悬臂梁在规定的挠度范围内服役。
设压电悬臂梁允许超过的向下最大挠度为wl,其对应的转角为θl,则压电悬臂梁上层压电层缩短位移为
(7)

压电悬臂梁下层压电层伸长位移为
(8)
式(7)和式(8)代入式(3)~式(6)分别计算得到在不同ΔEu和ΔEd下的压电悬臂梁的力学输出与电学输出。
压电悬臂梁中间铁芯在外界载荷下,允许的向下最大挠度为wl,其产生的抗力为
(9)
式中:L为悬臂梁铁芯的长度;E为铁芯的弹性模量;I为铁芯的惯性矩。
由式(3)~式(6)和式(9)可得到逆压电条件下压电悬臂梁的极限状态方程:
(10)
(11)

式(10)、式(11)计算所得可靠度为P(f)和P(J),由于压电悬臂梁既要考虑力学可靠又要考虑电学可靠,因此逆压电条件下的压电悬臂梁可认为由两者组成的串联系统。因此逆压电条件下压电悬臂梁的最终可靠度为
P=P(f)·P(J)
(12)
式(10)和式(11)是隐式方程,为方便计算,用一次二阶矩法进行进一步的简化运算。
3 逆压电条件下压电悬臂梁可靠度计算的简化
式(3)~式(9)中参数的均值与标准差如表1所示。

表1 式(3)~式(8)中参数的均值与方差

续表
假设表1中的所有参数都是无关的,则由式(3)~式(6)可得各式的均值与方差计算公式如下:
(13)
式中:
μu1=μc11μAuμΔuu
μu2=μe31μAuμΔEu
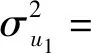

(14)
(15)
(16)
式中:
μd1=μc11μAdμΔμd
μd2=μe31μAdμΔEd


(17)

(18)
式中:
μu11=μe31μAuμΔuu
μu22=μΞ33μAuμΔEu

(19)

(20)
式中:
μd11=μe31μAdμΔud
μd22=μΞ33μAdμΔEd
由式(9)可得Δuu的均值与方差:
(21)
(22)
式中:
由式(8)可得Δud的均值与方差:
(23)
(24)
式中:

由式(9)可得F的均值和方差:
(25)
(26)
式中:
μElw=3μEμlμwl
由式(10)和式(11)得到逆压电条件下压电悬臂梁的力学可靠度计算公式:
(27)
式中:
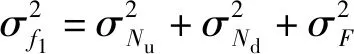
(28)
式中:μQJ、σQJ分别为QJ的均值与标准差;μQM=max{μQu,μQd};σQM=max{σQu,σQd}。
P(f)=P-1(βf)
(29)
P(J)=P-1(βJ)
(30)
由式(27)、式(28)及式(14)也可得逆压电条件下压电悬臂梁的可靠度。
4 算例
压电悬臂梁参数都服从正态分布,其均值如表2所示,变异系数为0.005[8]。

表2 压电悬臂梁参数及其均值
在不同电压下,由式(27)、式(28)计算所得可靠性指标与可靠度如表3所示。

表3 不同电压下的压电悬臂梁的力学与电学可靠度指标
由式(10)、式(11),用蒙特卡洛方法(MC)分别计算106次,所得可靠度如表4所示。
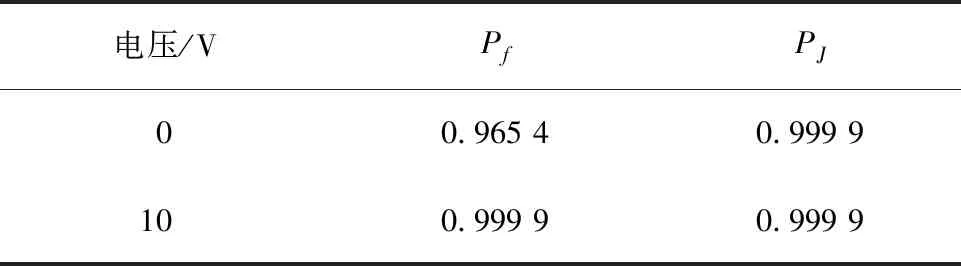
表4 MC计算不同电压下的压电悬臂梁的力学与电学可靠度
压电悬臂梁最终可靠度如表5所示。

表5 不同电压下的压电悬臂梁的可靠度
由表3可以看出,在未加电压的情况下,压电悬臂梁的初始设计的力学可靠度要比加电压之后的可靠度要低,而加电压之后,压电悬臂梁的可靠度要明显的提高不少,这也是设计智能压电悬臂梁的目的。对于电学可靠度来说,未加电压的可靠度表中显示是一样的,这是由于数据精度的原因,但实际上在仿真时,未加电压的可靠度要比加载电压的可靠度高,这是因为悬臂梁的压电层在空载状态下,加载电压后,悬臂梁的电学可靠度在使用状态下降低。从表4可以看出,本文处理方法与极限状态法结果一致,说明一次二阶矩法是可行的。表5根据串联系统原理,取得最后的可靠度,显示加载电压后的可靠度比未加载电压的可靠度高。
5 结论
文中给出了逆压电条件下压电悬臂梁的力学输出与电学输出数学模型;由逆压电条件下压电悬臂梁力学可靠性和电学可靠性计算的极限状态方程,按照串联系统可靠性计算方法,给出了逆压电悬臂梁的可靠度计算公式;利用一次二阶矩法,给出了逆压电状态下压电悬臂梁的的可靠度简便计算模型,2个算例说明,该模型简便易行,具有实用性和可行性。

