孔冷挤压有限元仿真中的铰削分界面位置确定方法
杜旭,张腾,何宇廷,张天宇,张胜,冯宇
空军工程大学 航空工程学院,西安 710038
螺栓孔、铆接孔是影响飞机结构寿命和服役使用安全的关键部位,紧固件连接孔发生疲劳断裂是飞机结构常见的失效形式之一。20世纪60年代,波音公司为了减缓飞机金属结构连接孔疲劳裂纹扩展,提出了开缝衬套冷挤压强化的基本概念。美国FTI(Fatigue Technology Inc.)在此基础上开发了更加经济高效的挤压强化工艺,并成功应用到了铝合金和高强度钢材料抗疲劳设计之中。80年代中期,FTI建立了完备的润滑开缝衬套孔冷挤压强化工艺流程和行业标准,从此该技术被国内外各大制造公司采用[1]。国内外学者针对开缝衬套冷挤压强化技术工艺改进[2]、工艺参数优化[3],以及挤压过程数值计算[4]、残余应力场获取[5]、疲劳寿命预测[6-9]和裂纹扩展行为研究[10-12]等方面开展了大量工作。近年来国内学者,在挤压强化铝合金、钛合金、高强度钢的残余应力分布、增寿效果研究方面,开展了大量有意义的工作[13-17],推动了挤压强化技术在中国航空制造等行业的应用[18-19]。
开缝衬套孔冷挤压强化是飞机结构制造维修中最常用的抗疲劳技术。其基本原理:将带润滑效果、轴向开缝的衬套装入待挤压孔中;然后用直径大于开缝衬套内径、硬度大于被强化材料的芯棒挤过连接孔。当芯棒挤过开缝衬套时,衬套张开并挤压孔壁,迫使靠近孔壁区域发生塑性变形;进而在孔边区域引入残余压应力层,实现改善结构受载后孔边应力状态,达到提高裂纹萌生寿命和阻碍裂纹扩展目的。孔冷挤压强化加工包括制预制(初)孔、孔挤压、铰制终孔和检查孔径4个基本工艺步骤。
开缝衬套可避免芯棒和孔壁接触摩擦,有效降低材料向芯棒挤入端和挤出端方向的塑性流动,极大改善残余应力沿厚度方向分布的均匀性;衬套内壁附着的润滑材料,可显著降低芯棒与衬套间的摩擦力,提高挤压加工成品率;同时衬套的存在,使芯棒工作段直径可小于预制孔径,让单边挤压加工成为了可能。工程采用的开缝衬套多由FTI供应,研究衬套加工制备工艺,尽快实现开缝衬套加工国产化,已迫在眉睫[18]。材料在衬套开缝处因发生塑性流动,而导致孔壁处形成“凸脊”。凸脊根部的微裂纹,在疲劳载荷作用下极易发生应力集中[4];凸脊的存在还会影响到紧固件的装配精度。铰制终孔作为挤压强化工艺中的关键环节[1],不仅能够去除凸脊,而且能改善挤压后孔的腰鼓状态,确保装配精度。铰制终孔势必会造成孔壁区域材料约束状态的变化,残余应力场的释放与重构。张飞[4]通过试验和数值计算,定量研究了铰制终孔工艺中铰削量对疲劳寿命的影响规律,指出不同挤压量下的最佳铰削量不同。
基于有限元法(FEM)的孔冷挤压过程数值计算是残余应力场获取的重要方法,相对于机械破坏法、X射线等残余应力测试方法,成本低效率高,且更容易获取沿厚度方向的残余应力分布规律[20-21]。通过数值计算获取挤压强化孔受载后应力集中度是进行疲劳寿命预测的关键,Sun等[9]和关迪[14]在各自的研究中,利用ABAQUS对挤压过程进行三维模拟,并利用ABAQUS软件的用户材料子程序(UMAT)功能,将连续介质损伤力学应用到铝合金强化孔疲劳寿命预测中,取得了满意的结果。朱海[8]针对飞机结构中最常见的连接结构,在对挤压过程三维模拟的基础上,采用应力场强法对连接孔进行疲劳寿命估算。Chakherlou等[22]基于强化结构三维有限元仿真,开展了双侧搭接结构中挤压强化孔的疲劳寿命预测工作。美国空军、加拿大和ersdTM高度重视挤压过程数值模拟方法和软件的开发,并在裂纹扩展分析软件中考虑了残余应力区的影响[11]。
孔冷挤压过程数值计算分为芯棒挤压、移除衬套和铰制终孔3个基本步骤,模拟挤压后精铰孔过程的铰制终孔步骤,是为了确保仿真得到的强化孔直径等于要求的终孔直径。常见的终孔铰销模拟方法有两种:一种是通过删除(Deleting)/杀死(Deactivating)单元层模拟铰制终孔过程;另一种是采用赋应力场法,将芯棒挤压、移除衬套模拟得到的残余应力场作为初始应力状态赋予未变形中心孔板,再删除预先划分的铰销层,模拟铰制终孔。王幸等[7]详细介绍了上述两种方法,并重点分析了不同单元删除方式对残余应力分布的影响。虽然赋应力场法简单易操作、计算成本低,但其无法考虑材料被挤压后的塑性变形,在仿真分析中采用较少。本文中所说的铰制终孔模拟,特指采用直接删除/杀死单元层法。
采用直接删除/杀死单元层法模拟铰制终孔时,需要在有限元建模阶段建立铰销单元层和基体材料单元分界面,将绞削层单元与基体分开;然后在完成芯棒挤压、衬套撤离模拟后,直接删除或杀死铰销层单元[7]。在孔挤压抗疲劳技术的工程应用中,通常依据终孔尺寸、预期增寿目标等,优化设计初孔尺寸和挤压量。由于挤压过程孔壁处塑性变形、卸载过程孔壁处回弹,以及芯棒和衬套压缩量的存在,准确确定铰削分界面相对位置就成为了一个难题。为了便于说明,用铰削分界面距挤压变形前孔壁的距离,表征分界面的相对位置。
确定铰削分界面相对位置的常规方法,是采用多次重复模拟孔冷挤压过程,在摸索中确定分界面位置,这将大大增加计算成本[7]。弹塑性力学分析为有效解决该问题提供了可能,本研究通过挤压强化过程弹塑性分析,得到了连接孔挤压强化过程的二维残余应力应变分布和径向位移变化量,据此建立了铰销分界面相对位置计算模型,并对模型关键参数进行了敏感性分析。
1 孔冷挤压强化过程弹塑性分析
在整个挤压强化工艺流程中,孔挤压步骤进一步可分为挤压和卸载两个基本过程。挤压过程中,开缝衬套和试件被芯棒挤压,并一起沿着径向膨胀;在卸载过程中,材料反向回弹。Guo[5]率先给出了带孔冷挤压孔有限平板的弹塑性分析模型,其强调了卸载过程反向屈服特性的重要性。Zhang等[23]在Guo[5]的模型基础上,详细介绍了卸载过程中应力分布模型,但并未考虑径向位移变形量对应力分布的影响。
1.1 材料的应力-应变行为描述
采用修正的Ramberg-Osgood模型[24]描述被挤压强化连接孔结构材料的应力-应变行为
(1)
式中:σ和ε分别为被挤压强化连接孔结构材料真实应力、应变;E为被挤压材料的弹性模量常数;σy为被挤压材料初始屈服应力;n为被挤压材料的应变强化指数。
1.2 弹塑性分析基础
衬套开缝处通常远离结构的危险截面,那么因开缝所导致的危险截面应力分布不均匀性将非常弱[25-26]。在弹塑性分析中可以采用全衬套代替开缝衬套,即挤压强化导致的径向和周向应力均匀分布。则待挤压连接孔将被简化为二维厚壁圆筒受内压的情形。径向应力σr和周向应力σθ满足
(2)
式中:r和θ分别代表极坐标下的径向方向和周向(环向)方向。
对应的径向应变εr和周向应变εθ满足
(3)
根据几何方程,应变分量εr、εθ与径向位移量u之间满足如下基本关系
(4)
(5)
塑性变形区的总应变为弹性应变εe和塑性应变εp之和
ε=εe+εp
(6)
塑性区的应变分量满足
(7)
(8)
根据Hooke定律,弹性应变与应力满足
(9)
(10)
式中:ν为被挤压材料的泊松比。
考虑因材料塑性流动导致的各向异性,塑性区应变和应力满足
(11)
(12)
式中:参数R用来描述材料塑性变形下的各向异性水平,其定义是平面塑性应变向三维塑性应变的转换比,当R=1代表各向同性;Et是单轴应力-应变曲线的切向模量,具体定义为
(13)
如式(9)和式(10)所示,应变由应力制约,那么泊松比ν的取值并不会影响到应力分量求解。令ν=R/(1+R),则弹塑性总应变的分量εr、εθ与应力分量间的关系可表述为
(14)
(15)
需要强调的是,根据σr、σθ计算弹性应变分量时,应采用被挤压材料真实泊松比ν。
1.3 挤压过程残余应力分析
芯棒和开缝衬套材料刚度相对较大,在弹塑性应力分析中,假设芯棒和衬套仅发生弹性变形。
1.3.1 衬套应力分析
挤压过程中,衬套受到如图1所示的内外均布压力作用。图1中ts为衬套厚度;D0为连接孔被挤压前的直径;D0-2ts为挤压时开缝衬套的内径;pm和ps分别为挤压时衬套内壁和外壁上的压力值。
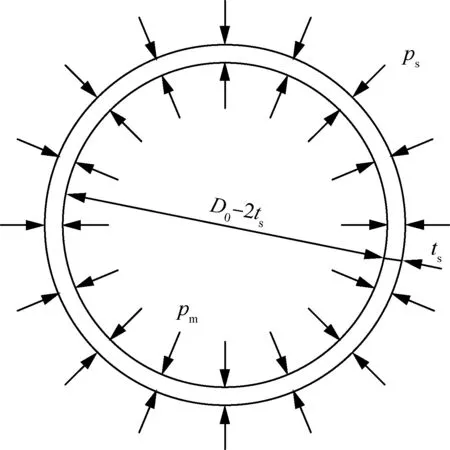
图1 挤压过程中衬套受内外压力作用Fig.1 Split sleeve subjected to internal and external pressures during extrusion
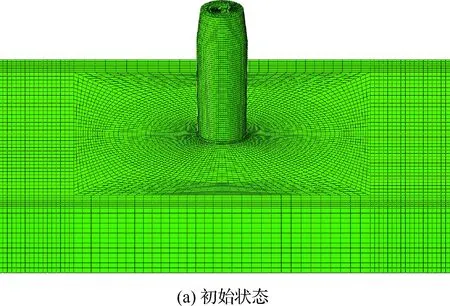
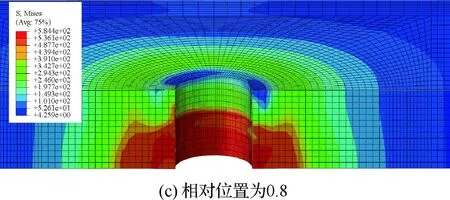
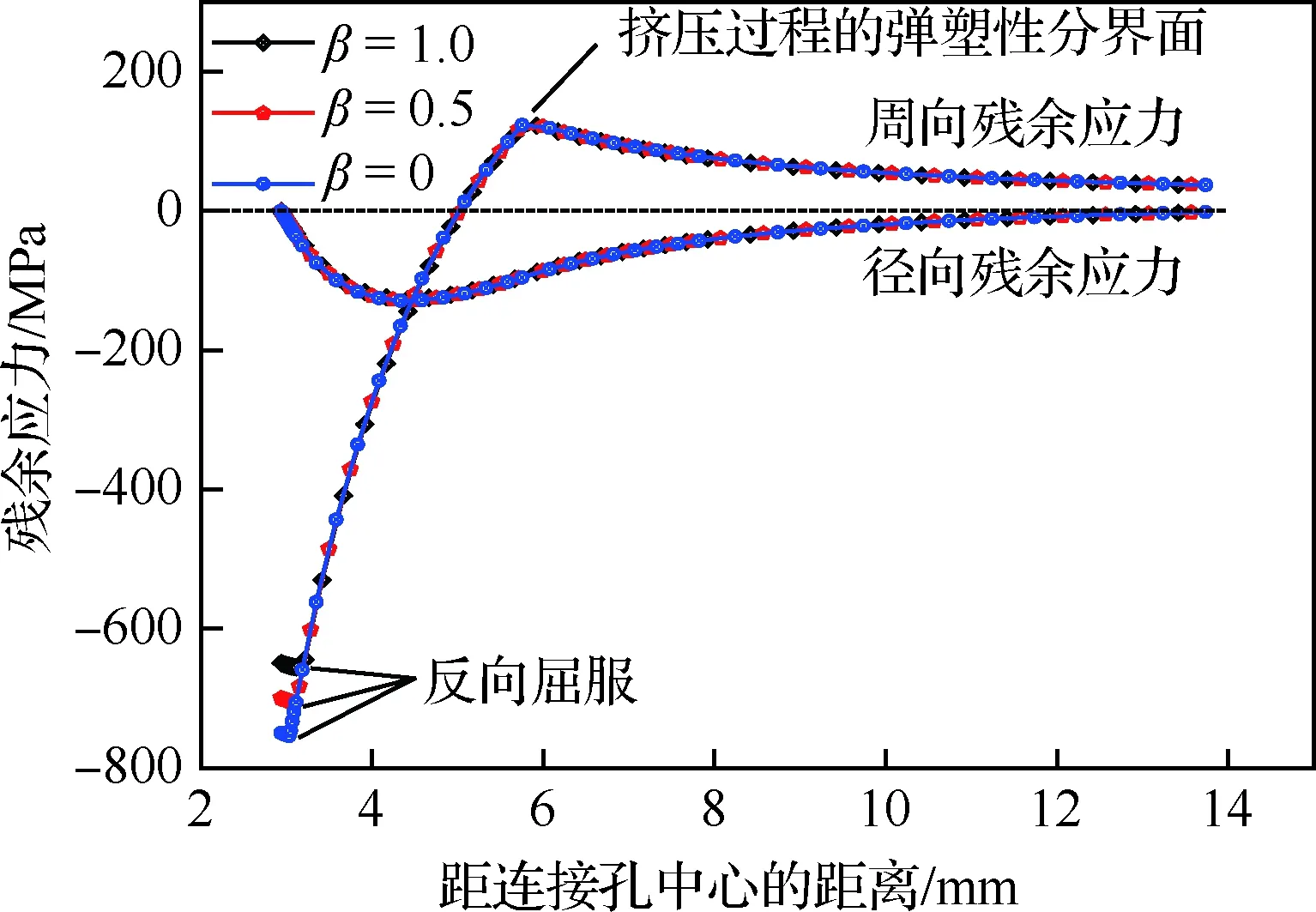
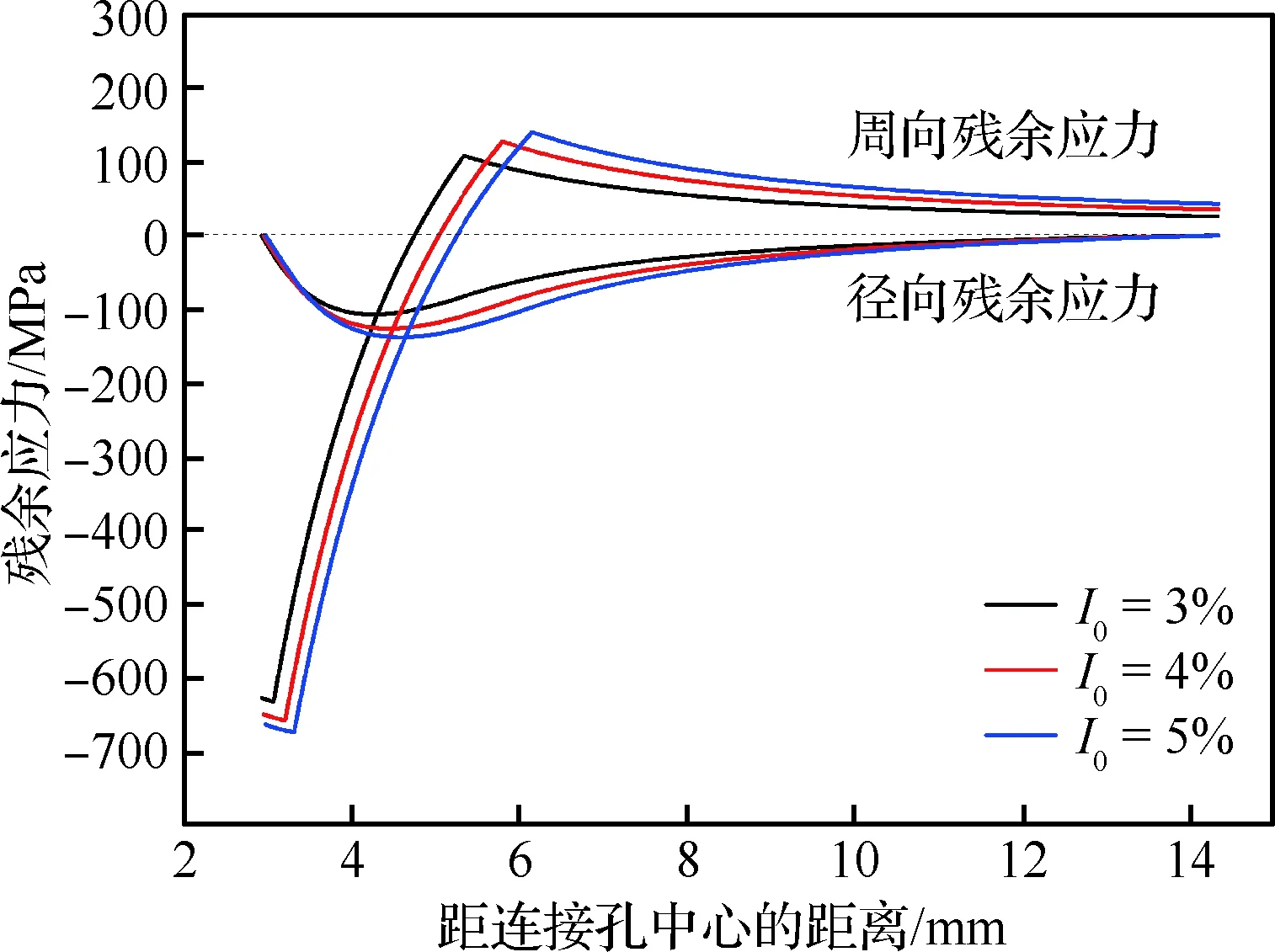
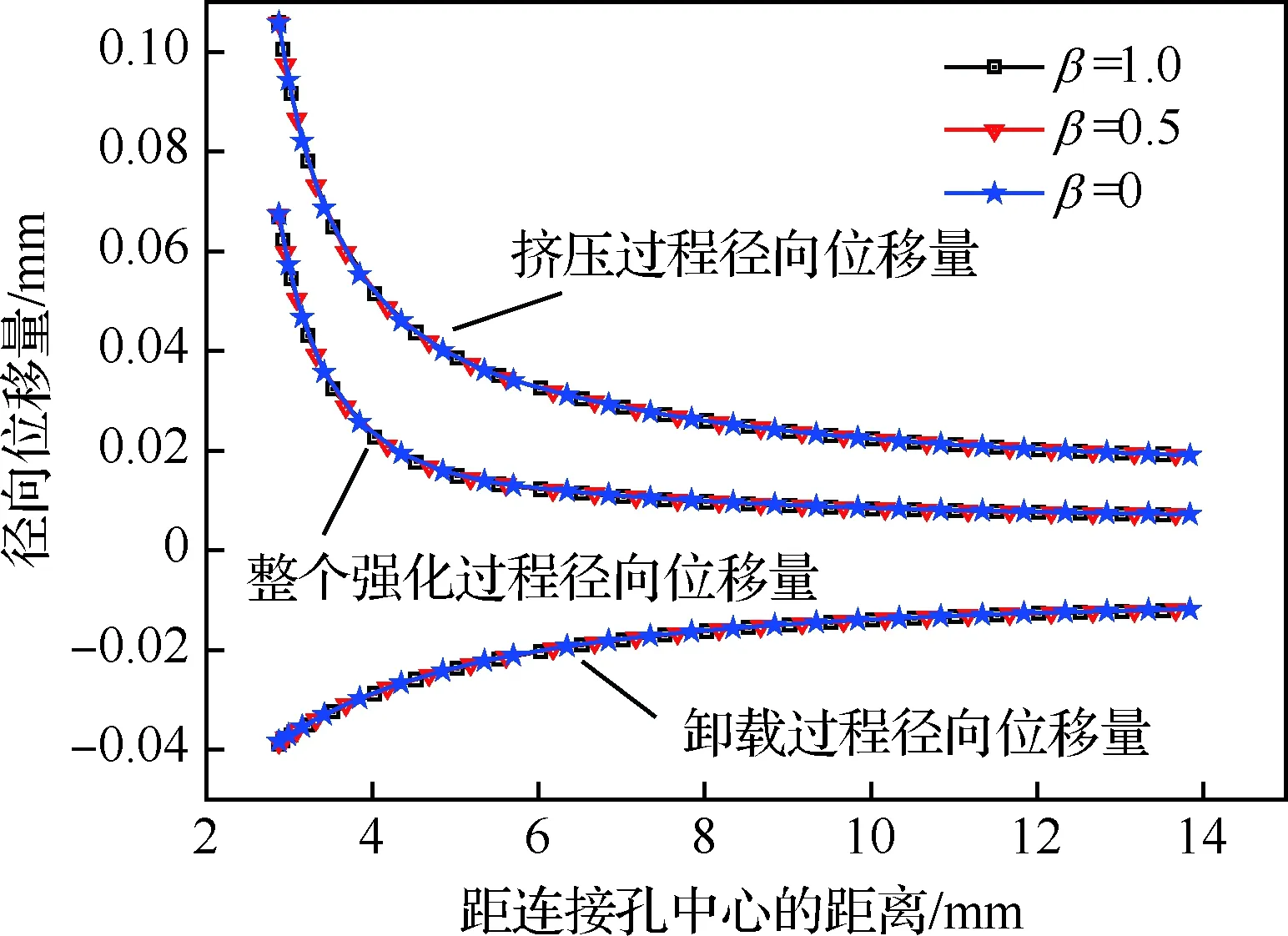
衬套厚度通常较小(0.15~0.25 mm),仅取衬套作为分析对象,不属于厚壁圆筒受压范畴。但在挤压过程中,衬套外壁紧贴连接孔孔壁,可以将衬套和连接孔看作一个整体。那么衬套就是厚壁圆筒中的一部分,在仅发生弹性变形情形下,衬套(a-ts (16) (17) 衬套内壁处(r=a-ts)的应力分量为 σr=-pm (18) (19) 那么,衬套内壁处的径向位移量为 us1= (20) 式中:Es和νs分别为衬套的弹性模量和泊松比。 衬套外壁处(r=a)的应力分量为 σr=-ps (21) (22) 那么,衬套外壁处的径向位移量为 us2= (23) 1.3.2 被挤压强化连接孔应力分析 芯棒挤压衬套内壁时,衬套向外膨胀挤压孔壁,靠近孔壁的区域发生塑性变形,远离孔壁区域则发生弹性变形。被挤压连接孔可简化为如图2所示,其中内径为a、外径为b,a代表连接孔的初孔半径(a=D0/2)、b代表分析区域大小。 图2 被挤压连接孔孔壁受内压示意图Fig.2 Schematic diagram of internal pressure on wall of worked hole edge 假设孔壁处(r=a)受到衬套外壁传递的均匀压力ps(ps>0)、外径处(r=b)的压力为零;并假设弹-塑性变形区虚拟分界线半径rp(a (24) (25) 塑性区内(a (26) 选择的材料屈服准则为 σ=σy (27) 根据弹塑性分界线(r=rp)上应力连续性,式(24)和式(25)确定的应力分量应满足式(26)和式(27),联立后有 (28) 将式(28)分别代入式(24)和式(25)中,则得到用rp表示的弹性区应力分量σr和σθ (29) (30) 基于关键参数α,Ball给出了极坐标系下塑性区应力分量σr和σθ解析式[29] (31) (32) 因此在弹塑性分界面上,可以得到用参数αp表示的应力分量。将其与式(29)和式(30)联立,则可得到rp和αp之间的三角函数关系为 (33) (34) 由式(14)和式(15),得 (35) 再联立式(2)和式(3),可得 (36) 将式(15)代入式(36),可得 (37) 再将式(13)、式(31)和式(32)代入式(37)中,经过微分运算得 (38) 对式(38)进行定积分运算: (39) 积分后得 (40) 基于式(40)可得塑性区(a≤r≤rp,αp≤α≤αa)内任意点的有效应力值,由孔壁处径向应力σr=-ps,则可得到孔壁处的压力为 (41) 将式(31)和式(32)代入式(2)中,可得 (42) 对式(31)进行微分运算,得到径向应力σr的微分形式 (43) 将式(40)和式(43)代入式(42)中,可得 (44) 对式(44)进行定积分: (45) 积分后得 (46) 当r=rp时,则可联立建立rp、αa和αp的关系 (47) 对式(47),假设b→∞、ps→∞、rp→∞,则可以得到αmax为 (48) 被挤压试件的孔壁处通常发生塑性变形,那么其孔边的径向位移量为 (49) 将式(10)、式(12)、式(13)、式(31)和式(32)代入式(49)中,则可得到孔壁处位移量为 (50) 式中:σa/σy根据式(40)可表示为 (51) 挤压过程中,衬套和孔壁一起沿着径向方向被挤压,那么衬套外径处的径向位移量应与被挤压试验件孔壁处径向位移量一致,即us2=ua。 1.3.3 芯棒应力分析 挤压过程中,假设芯棒仅发生弹性变形,则可将芯棒工作段受载情况简化为实心圆柱受均布径向压力作用。那么芯棒工作段壁面(r=d0/2)上的应力分量可表示为 σr=-pm (52) σθ=-pm (53) 根据式(52)和式(53),可以得到芯棒工作段圆柱边的应力分量,结合式(5)和式(10),则芯棒工作段圆柱边的径向位移量为um(um>0) (54) 式中:Em、νm分别为芯棒弹性模量和泊松比;d0为芯棒工作段直径。 1.4.1 边界条件 工程中,通常采用绝对挤压量Ia或相对挤压量I0描述挤压强化干涉程度。绝对挤压量Ia定义为芯棒工作端半径与开缝衬套厚度之和与初始孔半径D0/2之差。即 (55) 相对挤压量I0指绝对挤压量与初始孔径的百分比 (56) 根据终孔尺寸、预期增寿目标和连接孔材料性能等,优化确定的相对挤压量,常称其为设计相对挤压量,对应于设计绝对挤压量。对应于上述挤压过程的弹塑性分析,工程绝对挤压量Ia等于芯棒工作段位移量和衬套内壁处位移量之和 Ia=um+us1 (57) 值得说明的是,连接孔真实绝对挤压量为ua,其值通常小于设计绝对挤压量。 1.4.2 求解思路 确定弹塑性分界线位置是挤压过程求解的关键。挤压过程求解思路如图3所示。 图3 挤压过程求解思路Fig.3 Solution flow of expansion process 芯棒撤离后,被挤压材料会沿着径向发生反向回弹,该过程被称为卸载过程。卸载阶段,可能会发生纯弹性卸载或弹塑性卸载。在纯弹性卸载中,不发生反向屈服;弹塑性卸载中,材料发生反向屈服。 1.5.1 弹塑性卸载 假设卸载过程中材料发生反向屈服,则称其为弹塑性卸载。 1) 反向屈服准则 弹性变形区发生反向屈服的条件为 σy′=σy+σ (58) 式中:σ为挤压过程产生的最大有效应力。 根据Ball的基本理论,塑性区的反向屈服准则为 σy′=(1+β)σy+(1-β)σ (59) 式中:β为包申格效应参数,且0≤β≤1。当β=0代表各向同性强化模型;β=1代表随动强化模型,研究表明随动强化模型可以较好的描述材料卸载行为中的包申格效应。 分析表明,卸载阶段中反向屈服通常发生在挤压产生的塑性区内,下述重点介绍该情况。 2) 反向屈服分界面确定 类似于挤压过程的弹塑性分析,在弹塑性卸载过程中,r=a′(α=αa′)处的压力值-ps与卸载过程弹塑性分界面r=rp′(α=αp′)的屈服应力σy′关系为 (60) 卸载过程弹塑性分界面对应的rp′、αp′与孔边对应的a′、αa′关系为 (61) 式中:a′为挤压后孔壁距离连接孔中心的距离。 3) 卸载过程塑性区应力 弹塑性卸载中,塑性变形区(a′≤r≤rp′)的应力分量为 (62) (63) 其中有效应力σ′为 (64) 类似于挤压过程,r、α′与a′、αa′的关系为 (65) 4) 卸载过程弹性区应力 弹性变形区(rp′≤r≤b)应力分量为 (66) (67) 卸载过程求解思路与1.4.2节所示的挤压过程求解思路基本一致,在此不再赘述。 1.5.2 纯弹性卸载 假设卸载过程中材料发生未反向屈服,则称纯弹性卸载。纯弹性卸载中,孔壁处的边界条件为 σr=-p (68) 则纯弹性卸载中的应力分量为 (69) (70) 根据应力叠加原理,整个孔冷挤压抗疲劳强化过程中的残余应力为 Δσr=σr+σr′ (71) Δσθ=σθ+σθ′ (72) 基于解析法获取的应力应变分析结果,建立了铰销层单元与基体材料单元之间分界面相对位置的确定模型。 假设距连接孔中心距离为r0的微单元,挤压过程中的径向位移量为ΔrL(r0)(ΔrL(r0)>0)。根据上述分析,塑性区的径向位移量为 ΔrL(r0)= (73) 弹性区的径向位移量为 (74) 距离连接孔中心r0处的微单元,经过挤压过程后,距离连接孔中心的距离为 rL(r0)=r0+ΔrL(r0) (75) 卸载过程,ΔrL(r0)处微单元的回弹位移量表示为ΔrU(r0)(ΔrU(r0)<0)。根据上述分析,卸载过程反向屈服塑性区的径向位移量为 ΔrU(r0)= (76) 弹性区的径向位移量为 (77) 那么,距连接孔中心r0处的微单元,经过挤压过程和卸载过程后,距离连接孔中心的距离为 rU(r0)=r0+ΔrL(r0)+ΔrU(r0) (78) 假设工程要求的终孔直径为Dz,根据式(79): r0+ΔrL(r0)+ΔrU(r0)=Dz/2 (79) 求解得到未知数r0,即为铰销层单元与基体单元之间的分界面距里连接孔中心的距离,r0与初孔半径之差(r0-d0/2)即为铰销层厚度。由于式(79)的高度非线性,通常可采用插值法确定未知数r0。 选取下述实例进行分析,对6.35 mm厚带中心孔的7075-T6铝合金板材进行挤压强化,要求连接孔终孔直径为6 mm。经优化分析,初孔直径为5.738 mm、开缝衬套厚度为0.152 mm、芯棒工作段直径为5.664 mm,设计相对挤压量为4%。 根据文献[9]相关数据,7075-T6铝合金弹性模量E=71.5 GPa、泊松比ν=0.33、初始屈服应力σy=503 MPa、应变强化指数n=16.44。选择的芯棒材料弹性模型Em=210 GPa、泊松比νm=0.295,开缝衬套材料弹性模型Es=210 GPa、泊松比νs=0.295。 2.4.1 残余应力分布 通过芯棒挤压和开缝衬套移除过程弹塑性有限元模拟,可以准确获取被挤压连接孔的残余应力分布状态。在对本实例数值计算中,芯棒挤压移动到的不同相对位置下,孔边等效Mises应力分布如图4所示。提取得到的入口层、中间层和出口层的残余应力分布分别如图5和图6所示。 取参数b=5a=14.345 mm、包申格效应参数β=1,利用本文的残余应力分析方法得到的径向和周向残余应力分布分别如图5和图6所示。 图4 芯棒不同相对位置下孔边等效 Mises应力云图(MPa)Fig.4 Von Mises stress at different normalized mandrel positions (MPa) 图5 径向残余应力分布对比Fig.5 Comparison of radial residual stress distributions 图6 周向残余应力分布对比Fig.6 Comparison of hoop residual stress distributions 图5和图6中对比,本文模型得到的残余应力分布规律与有限元方法中间层吻合度较好,印证了残余应力理论解析模型的正确性。 2.4.2 铰削分界面位置确定 在本实例弹塑性理论解析模型分析中,挤压过程、卸载过程以及两个过程叠加后的径向位移量如图7所示。 图7 不同过程径向位移量Fig.7 Radial displacement at different stages 由图7可知,挤压过程径向位移量与卸载过程方向相反,即挤压过程导致材料沿径向方向扩张,而卸载过程相反。虽然卸载过程径向位移量的绝对值明显小于挤压过程,但在铰削分界面位置确定中是不能被忽略的。 以图7中数据为基础,以挤压变形前微单元距孔中心的距离为横坐标,以挤压强化后微单元距孔中心的距离为纵坐标,建立如图8所示的对应关系图。 图8 挤压前后微单元距连接孔中心距离对应关系Fig.8 Corresponding relationship of the distance from hole center to micro-elements before and after expansion 在基于图8的绞削分界面相对位置确定中,终孔孔径尺寸是目标值,即当纵坐标值等于目标值时,所对应的横坐标值即为分界面距连接孔中心的距离。值得说明的是,该方法与基于式(79)的插值法在本质上没有区别。 包申格效应参数β、相对挤压量I0是残余应力分析和分界面位置确定中的关键参数,需要对其进行敏感性分析。 定量开展包申格效应参数β和相对挤压量I0的敏感性分析,确定其对残余应力分布的影响。 3.1.1 包申格效应参数β 在采用式(59)描述材料卸载反向屈服行为时,参数β将影响到中反向屈服应力的大小。基于2.4节实例,计算得到的不同β取值下的径向和周向的残余应力分布如图9所示。 由图9不难发现,参数β对周向残余压应力的最大值以及最大值分布位置有较大的影响,而对径向残余应力分布影响较小。因此,在采用该模型进行残余应力分析时,要确保选取的参数β能准确描述材料卸载中的反向屈服行为。 图9 不同β取值下残余应力分布Fig.9 Residual stress distribution of different parameters of β 3.1.2 相对挤压量 取参数β=1,改变设计相对挤压量I0的取值,计算得到的不同相对挤压量下的残余应力分布规律如图10所示。 图10 不同挤压量I0下残余应力分布Fig.10 Residual stress distribution at different interference ratios I0 根据图10易知,相对挤压量I0对周向残余压应力区域大小和塑性变形区域大小影响较大,但是对残余压应力值的最大值影响有限。该结论与Amrouche[30]的结论基本一致,但王强等[3]研究结果却表明,挤压量对残余应力区域和峰值均有较大影响。因此挤压量对周向残余压应力分布的影响规律,还需要进一步通过残余应力测试加以研究。 周向残余压应力对增寿效应的显著贡献度已经得到了同行的普遍认同。相关研究表明,对铝合金而言4%左右的相对挤压量时,增寿效果最显著[31]。由图10可知,随着挤压量从3%~4%的增大中,虽然周向残余压应力最大值变化不大,但是增寿效果非常显著,这是由于残余压应力区域显著增大了,极大改善了结构受载后孔边的应力分布状态。 挤压过程和卸载过程的径向位移量是铰削分界面位置确定模型中关键变量。进行铰削分界面确定模型敏感性分析,实质上是进行关键参数对挤压强化过程径向位移量的敏感性分析。 3.2.1 包申格效应参数β 参数β不同取值下,挤压过程、卸载过程和叠加后的径向位移量如图11所示。 图11 不同β取值下径向位移量Fig.11 Radial displacement at different values of parameter β 由图11可知,包申格效应参数β不影响挤压过程的径向位移变化量,这是由于参数β控制的是卸载中的反向屈服行为。参数β的变化会影响反向屈服应力大小,进而影响到卸载过程径向位移量的大小。值得说明的是,参数β的变化对径向位移量影响效应相对较弱,且卸载过程径向位移量的绝对值相对较小,因此在图11中,不同参数β取值下的卸载过程径向位移量曲线近似重叠。 3.2.2 相对挤压量 取参数β=1,改变相对挤压量I0值,得到了3种取值下的径向相对位移量,具体情况如图12所示。 图12 不同相对挤压量I0下径向位移量Fig.12 Radial displacement under different interference ratios I0 根据图12不难发现,相对挤压量越大,挤压过程、卸载过程的径向位移量绝对值也就越大,这与理论分析结果一致。 1) 本文建立的绞削分界面相对位置计算模型,为有限元建模阶段设置铰削分界面提供了有效方法。 2) 相对挤压量I0对周向残余压应力区域和塑性变形区域大小影响较大,但对残余应力值的最大值影响有限。随着I0从3%~4%的变化中,残余压应力区域显著增大了,结构受载后孔边应力状态将得到显著改善。 3) 包申格效应参数β是描述卸载屈服行为的关键参数,特别是对周向残余应力最大值以及最大值的位置有较大影响。因此在使用本文模型,获取二维残余应力分布或计算铰削分界面相对位置时,采用的模型要能准确描述材料卸载中的反向屈服行为。


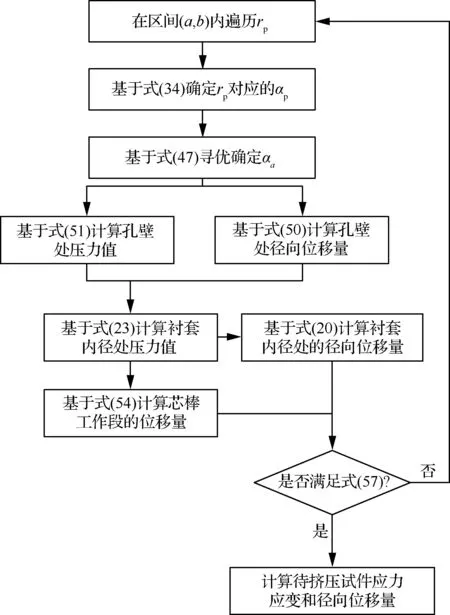
1.4 边界条件与求解
1.5 卸载过程应力分析
1.6 残余应力
2 铰销分界面位置确定方法
2.1 挤压过程径向位移量
2.2 卸载过程径向位移量
2.3 铰销层厚度确定方法
2.4 实例分析






3 分析与讨论
3.1 残余应力分析模型敏感性分析
3.2 铰削分界面确定模型敏感性分析

4 结 论

