基于动力学边界的结冰飞机安全预警方法
郑无计,李颖晖,周驰,武朋玮,董泽洪
空军工程大学 航空工程学院,西安 710038
飞机结冰破坏飞机的气动特性,使升力降低、阻力增加,同时使飞机失速迎角大幅度下降,恶化飞机的飞行性能,导致传统的边界保护系统和操纵方法失效,因此对飞行安全造成严重的威胁[1],另外由于飞机结冰导致的飞行事故具有强破坏性[2]和高发性[3],因此引起了广大航空领域专家学者对飞机结冰后飞行安全问题的关注。国外对飞机结冰机理[4-5]、气动特性影响[6-8]、防/除冰方法[9]、动力学特性[10-13]等相关理论的研究较早且涉猎内容较为广泛,而国内针对结冰飞机相关理论的研究起步相对较晚且致力于对飞机防/除冰系统[14]及致灾机理方面[15-17]的研究,针对飞机结冰后动力学特性的研究相对较少,然而这部分内容却对提高结冰飞机的飞行安全十分重要。
Bragg教授团队[10, 18]指出从规避结冰条件和带冰飞行两方面入手可有效减少或防御结冰引起的飞行事故,其中通过规避结冰条件来防止飞机结冰事故是非常理想的方法,但在一定程度上是无法实现的[18-19],因此研究飞机带冰情况下的动力学特性是至关重要的。另外,飞机结冰使飞机飞行品质下降,导致驾驶员无法准确评估飞机的动力学特性,因此也经常发生由于驾驶员误操纵而引发的飞行事故。例如:2002年台湾复兴航空的ATR72-200飞机由于机翼严重结冰而失速坠海;2006年在安徽地区同样因为机翼严重结冰引发重大飞行事故。
为解决飞机带冰飞行问题,首先必须获得结冰飞机准确的气动特性。鉴于此,2000年NASA[20]关于飞机结冰的报告中详细地分析了飞机结冰对气动特性的影响,与此同时Bragg团队[10]提出了结冰飞机气动参数的结冰因子影响模型,为后续对结冰飞机的动力学特性及边界保护的研究奠定了坚实的理论基础。在此基础上,2008—2010年,美国田纳西州大学(University of Tennessee Space Institute,UTSI)与Bihrle应用研究(Bihrle Applied Research, BAR)技术公司合作,构建了结冰污染边界保护系统[21-22](Icing Contamination Envelope Protection system, ICEPro),提出了结冰边界告警与保护方法。
另外,综合分析上述边界保护系统及相关理论的文献可知[13, 18, 23-25],构建精确、有效的边界保护系统,必须有可靠的飞行风险预警预测方法。然而现有飞机装备的边界保护系统很难准确评估结冰情况下的潜在危险,例如1994年的ATR72事故[26],该飞机由于结冰导致迎角为5°时就发生了滚转异常现象并最终导致飞行事故。而文献[27]提出了一种基于微分流形理论确定的可考虑飞行状态耦合情况的动力学边界,并初步确定了飞机结冰情况的动力学边界。因此,本文在微分流形理论确定的动力学边界基础上详细分析了结冰对该动力学边界的影响,提出基于动力学边界进行结冰飞机飞行风险评估的方法,并以此为基础结合飞行仿真相关理论构建结冰飞机的飞行仿真训练系统;以着陆为测试科目对系统的正确性进行验证,最后利用该系统初步对驾驶员的结冰风险感知能力进行训练。结果表明该系统可对驾驶员进行结冰应对策略训练,可为结冰飞机飞行训练模拟器的构建提供理论支撑。
1 基于流形理论的结冰飞机动力学边界
稳定域作为微分动力学系统稳定与不稳定的界限,充分地反映出微分动力学系统空间状态的运动趋势,而飞机本质为复杂微分动力学系统,其飞行包线在一定程度上也具有分割安全飞行与不安全飞行的性质,因此可利用微分动力学系统的稳定域作为飞机的某种飞行包线,因稳定域考虑了飞机的动力学特性且考虑国际上类似的概念,取名为动力学边界(即国际上所用的Dynamic Envelope)。
1.1 流形理论
流形理论是根据微分系统的空间拓扑结构确定系统稳定平衡点吸引区的一种方法,它利用直接积分方法得到边界上不稳定平衡点的稳定流形作为稳定边界的一种精确估计[1]。针对稳定平衡点稳定边界上具有多个不稳定平衡点的情况,通过依次计算边界不稳定平衡点上的稳定流形,最终以所有稳定流形的并集所包围的区域作为该稳定平衡点的稳定域。因此,基于流形理论计算稳定域即飞机动力学边界的难点在于边界上不稳定平衡点稳定流形的计算。现今针对不稳定平衡点稳定流形的计算较多[28],且优缺点各异,其中逆轨迹法效率较高但在一定程度上限制了算法的精度,本文在此基础上以MATLAB仿真平台为依托对逆轨迹法终点进行校正,并利用并行算法快速计算飞机的动力学边界,提高计算精度的同时提高了计算效率,具体计算方法如下。
考虑如下形式的非线性系统
(1)
式中:
x=[x1x2…xN]T
(2)
1) 通过求解非线性方程组f(x)=0,得到系统的平衡点,并通过f(x)在平衡点的Jacobian矩阵特征值的情况判断平衡点的稳定性,并确定不稳定平衡点的型别。
2) 判断不稳定平衡点是否位于稳定平衡点的边界上。
3) 利用稳定边界上的1型不稳定平衡点的稳定流形确定系统的稳定边界。
下面以稳定流形的计算为例说明本文的二维流形的计算方法(对于流形而言,一维为线,二维为面,三维为体,因本文主要研究不同速度情况下,迎角、俯仰角及俯仰角速度的动力学边界,为空间曲面,故此处应为二维流形):
1) 计算向量场f(x)的雅克比矩阵D,得到特征值及其对应的特征向量分别为ε1、ε2、ε3和v1、v2、v3。并设ε1>0、ε2、ε3为小于零的实数或实部小于零的共轭复数。
2) 计算流形初始平面的法向量ξ:ε2、ε3为小于零实数,此时ξ=v2×v3;ε2、ε3为共轭复根,此时ξ=(v2+v3)×[(v2-v3)i],i为复数单位。
3) 确定稳定流形初始点。以不稳定平衡点(Unstable Equilibrium Point,UEP)为原点在法向量ξ确定的平面上取圆形,并在圆周上均匀取点作为稳定流形的初始点。
4) 计算圆形轨线并进行校正。利用反时间系统计算每个初始点解轨线,并在达到特定长度l后停止本次计算,并对轨线终点进行校正,以便得到光滑的圆形轨线。校正方法如下:
① 计算终点校正时间tadd
(3)
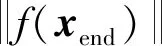
② 计算终点的校正点xnew
xnew=xend+taddf(xend)
(4)
5) 计算相邻解轨线终点的距离d,并作如下判断(Δ为圆形轨线的相邻点的距离限制,其选择主要是为了避免轨线点过少引起的计算误差以及轨线点过多而引起的计算资源浪费,一般取每单位轨迹圆100~200点为宜):
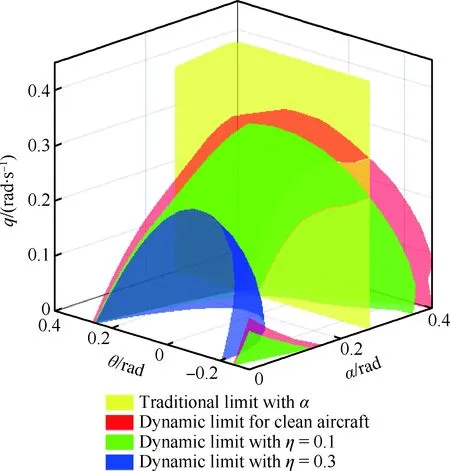
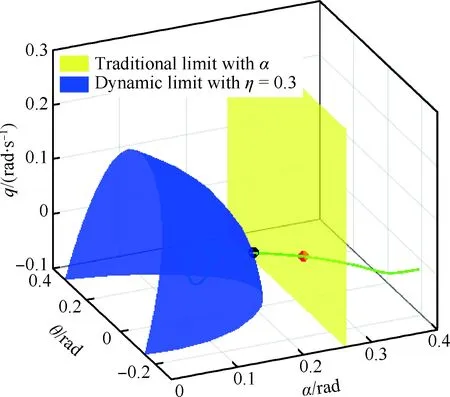
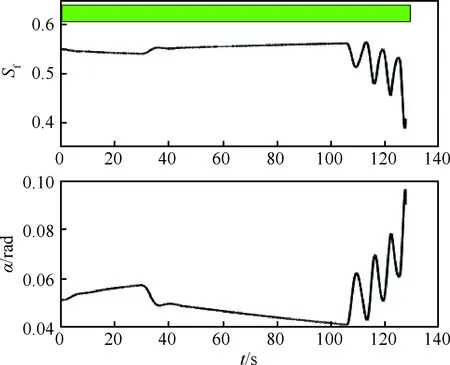
① 如果0.5Δ ② 如果d>1.5Δ,则在相邻两点之间插入round(d/Δ)-1个点,其中round(x)函数为通过四舍五入的方法取整; ③ 如果d<0.5Δ,则舍去该点。 注:第4)、5)步采用并行算法,可同时计算圆形轨迹上的点和距离。 6) 通过上述计算得到完整的圆形轨线,并以该圆形轨线为初始轨线重复第4)、5)步过程,直到计算总长度Nl达到预定距离。 将上述N+1个圆形轨线连接成面,即为所求的二维稳定流形。 以NASA用于研究飞机失控的GTM(Generic Transport Model)[29-30]飞机的纵平面运动模型为对象,验证上述算法的效率及精度,最终本文所采用的动力学模型及参数为 (5) 式中: (6) δe=kαΔα-kqq+kθ(θref-θ) (7) 式中:反馈参数kα=-2,kq=-1,kθ=-3;Δα=α0-α为控制误差;θref为控制指令。 以大飞机打开15°襟翼、飞行速度Vt=85 m/s、高度H=400 m的下滑飞行任务为例,验证上述方法的精度和效率。本文研究的飞行状态具体如下: (8) 式中:δth为推力系数。 计算该状态下的平衡点分布情况,其中平衡点分布结果如表1所示,表中Type表示不稳定平衡点的型别。 表1 系统平衡点的分布Table 1 Distribution of equilibrium points for system 在不稳定平衡点添加小扰动得到动态响应曲线,并根据最终的收敛情况确定稳定平衡点边界上的不稳定平衡点,其中不稳定平衡点的动态响应结果如图1所示。 在UEP1添加扰动后所有的飞行状态都是发散的,而在UEP2、UEP3和UEP4添加扰动后存在飞行状态最终收敛于稳定平衡点的情况。结合表1最终确定边界上的1型不稳定平衡点为UEP2和UEP4,利用1.1节方法确定该飞行情况下的动力学边界(图2),并与Monte Carlo方法确定的动力学边界对比验证本文方法的精确性(图3)。 图1 动力学边界上的不稳定平衡点确定Fig.1 Determination of UEPs on dynamic envelope 图2 大飞机下滑阶段动力学边界Fig.2 Dynamic envelope for large aircraft during gliding phase 图3 动力学边界精确性验证Fig.3 Accuracy verification of dynamic envelope 如图2所示,为利用流形理论确定的飞机动力学边界。其中红色曲面为1型不稳定平衡点UEP2的稳定流形(Manifold 1);蓝色曲面为1型不稳定平衡点UEP4的稳定流形(Manifold 2),两者的交线为2型不稳定平衡点UEP3的稳定流形且在交线附近光滑过度。综上说明本文方法适用于处理类似飞机这类多平衡点系统。 如图3所示,为本文流形方法与Monte Carlo方法确定动力学边界的对比图。其中Monte Carlo法是在状态空间内取大量飞行状态点,并通过飞行状态点的动态响应是否收敛于稳定平衡点来判断飞行状态的安全性,并认为收敛于稳定平衡点的飞行状态是安全的,且所有安全飞行状态所构成的边界为本文所确定的动力学边界。通过对比可知,所有安全的飞行状态均在本文确定的动力学边界内,且安全的飞行状态边界与本文方法确定的动力学边界完美重合,因此可以证明本文方法具有较高的精度。另外根据动力学边界内飞行状态动态响应的收敛性可说明该动力学边界的安全特性,即动力学边界为动力学意义上飞行状态安全与不安全的分界线,这在一定程度上为在线飞行风险评估与安全预警提供理论支撑。 最后,利用逆轨迹和Monte Carlo法在Intel(R) Core(TM) i7-4690 CUP、主频3.6GHz、8 GB内存的台式机上进行相同工况的动力学边界仿真计算,通过对比(如表2所示),最终可说明本文方法具有较高的计算效率。 表2 计算时间Table 2 Calculation time s 飞机结冰导致气动特性被破坏,这也是导致飞行事故的原因之一,因此研究结冰飞机的动力学特性必须有准确合理的结冰飞机气动参数。2000年Bragg教授[10]提出的基于结冰因子的结冰飞机气动参数确定方法,在一定程度上解决了该问题,且被广大学者所接受,因此本文研究采用结冰因子方法确定结冰飞机的气动模型,其表达式为 CA,iced=(1+ηfice)CA (9) 式中:CA和CA,iced分别为结冰前、后飞机气动导数值;fice为结冰系数,反映CA对结冰的敏感性,对于给定的飞机为常值;η为结冰因子。 利用1.2节的控制方法对带冰飞机在高度H=400 m、打开15°襟翼,且以飞行速度Vt=85 m/s、 下滑角为2.5°稳定下滑为研究对象,确定结冰因子分别为0.1和0.3时的动力学边界,见图4。 如图4所示,飞机结冰后动力学边界收缩,尤其是结冰较为严重的情况下(η=0.3),动力学边界收缩较为明显且边界状态的耦合较为严重,因此在这种情况下进行操纵将有较高的风险,具体的风险评估方法见第2节。 图4 结冰程度对飞机动力学边界的影响Fig.4 Influence of different icing degree on aircraft dynamic envelope 对飞机系统而言,本文使用的动力学边界为该飞机微分动力系统的稳定域,因此根据稳定域的特点及上述相关论述可知,动力学边界内部的飞行状态将在有限时间内收敛于稳定平衡点,即飞机的工作点。且飞机飞行状态离边界越近,飞机越容易因外部扰动或驾驶员误操纵而引发飞机失控现象的发生。因此可利用飞行状态距动力学边界的距离表征此时飞行状态的飞行风险,即距离动力学边界越近则相对飞行风险越高,离动力学边界越远则相对飞行风险越低。考虑到动力边界的复杂性且无隐式或显式表达,本文采用如下方法对飞行风险进行量化,并称该方法为基于动力学边界的飞行风险评估方法,其几何概念图如图5所示。图中点S为稳定平衡点(用xs表示);点F为飞机实时的飞行状态(用xf表示);点E为SF与动力学边界的交点(用xe表示),其中飞行情况①为安全飞行情况,此时点E为状态空间内射线SF与动力学边界的交点,点E位于SF延长线上;飞行情况②为危险飞行情况,此时点E为状态空间内SF与动力学边界的交点,点E位于点S和点F中间。 图5 安全系数的几何概念Fig.5 Geometric definition of safety factor (10) 式中:Sf为飞行状态的安全系数(Safety factor),用于量化飞机飞行过程中的风险等级。 图6 飞行风险等级划分Fig.6 Grades of flight risk 传统飞行安全预警方法通常对迎角进行限制,限制值一般为略小于失速迎角的可用迎角,但该极限值不能随飞机所处环境的变化而变化,也无法反映出飞行状态之间的耦合关系,因此具有一定的局限性。而本文的安全预警方法可保证迎角在不超出限制的情况下,提前发出危险告警,尤其是飞机飞行状态耦合较为明显的情况下效果更为明显,因此,在一定程度上可提高飞行安全,具体原因可结合图7进行说明。 图7所示为结冰飞机动力学边界限制与传统的迎角限制的对比图。其中黄色铅垂面为传统意义上的迎角限制面(本文GTM飞机的失速迎角约为0.312 rad,故本文取可用迎角为0.262 rad),即飞行状态位于平面左侧时为安全飞行状态(α<0.262 rad);图中红色、绿色以及蓝色曲面分别为无冰、结冰程度0.1以及结冰程度0.3时的动力学限制,此时安全裕度设定为0.2;且当飞行状态在动力学限制范围内时为安全飞行状态,超出该动力学限制后开始发出危险告警,提示驾驶员此时飞行状态已经具有潜在的飞行风险。由图7可知,俯仰角和俯仰角速度较大时,迎角的可用范围收缩且低于传统迎角的限制值,且可用迎角范围随结冰程度的加剧而大幅度收缩,尤其是结冰较为严重的情况下,动力学限制的迎角可用范围完全位于传统可用迎角限制值的左侧,此时使用传统的飞行风险评估及预警方法将极易导致飞行事故,而使用动力学限制的安全预警方法在一定程度上可解决类似问题的发生,下面结合图8~图10说明此问题。 图7 结冰情况下动力学限制与传统迎角限制对比Fig.7 Comparison between dynamic limit and traditional angles of attack limit under icing condition 图8所示为结冰飞机匀速下滑阶段驾驶员进行拉杆操纵后的俯仰姿态响应曲线,且在飞行状态在55.5 s左右超出可用迎角限制;图9所示为相同情况的三维响应,且可知飞行状态首先超出本文使用的动力学限制,随后才超出传统的可用迎角限制;图10所示为此时飞行情况下基于动力学限制的安全预警方法和传统可用迎角限制安全预警方法的对比图,可知飞行状态在40 s左右超出动力学限制的安全裕度值0.2(该裕度值的设定与传统可用迎角裕度设置相同)。 图8 时域仿真验证Fig.8 Verification based on real time simulation 图9 时域仿真结果三维显示Fig.9 Results of real-time simulation in three-dimensional viewpoint 图10 安全风险指标对比图Fig.10 Comparison of safety risk indicator 由图8~图10可知,采用基于动力学限制的安全预警方法将在仿真开始后的40 s左右发出危险告警,而使用传统迎角限制的安全预警方法将在55.5 s左右发出危险告警,因此在该飞行情况下,本文提出的安全预警方法相比于传统的安全预警方法将提前15.5 s左右发现飞行风险。为进一步说明本文方法的普适性及工程应用意义,后文将采用飞行模拟的方式对其在不同飞行情况下的优越性进行验证。 基于MATLAB/Simulink和Flightgear仿真软件搭建结冰飞机的飞行仿真训练系统(如图11所示),并通过大量仿真训练说明并验证动力学限制安全预警方法的优越性并初步实现对结冰感知能力的训练,为说明本文设计的飞行仿真系统在分析飞机着陆过程运动特性的适用性和飞行训练效果,驾驶员由本文作者担任并进行如下仿真训练(本文作者为没有任何飞机驾驶经验的学者,但掌握飞机着陆过程涉及的相关理论知识)。 本文采用拉飘[31]的着陆方式进行着陆,仿真从飞机位于海拔400 m高度、以2.5°航迹俯仰角和85 m/s速度稳定下滑开始,到飞机后轮接触地面结束;着陆过程中,驾驶员在飞机位于海拔高度15 m左右时,对飞机进行拉飘着陆的相关操纵。为说明训练效果并验证使用动力学限制后模拟器的可用性,进行大量的着陆训练,最终得到如下形式的着陆曲线。利用此训练系统得到飞机未结冰情况下的某一着陆轨线如图12所示,且此时2种安全预警方法的指示曲线如图13所示。 图11 结冰飞机飞行仿真训练系统结构图Fig.11 Structure chart of flight simulation training system for icing aircraft 由图12(x为航向距离)可知此时飞机的着陆轨线满足着陆标准,飞机接触地面时的下沉速度0.561 m/s同样满足设计要求,且通过对飞行状态的综合分析可知,利用本文设计的仿真系统进行着陆过程的相关研究是可靠、有效的。 图13所示为飞机未结冰情况下,着陆过程中本文设计的安全预警方法和传统安全预警方法显示结果的对比。由图可知,2种方法均未达到安全预警限制范围,且变化趋势基本一致,因此说明本文提出的安全预警方法不会影响飞机的正常飞行,这也为该方法的工程应用提供前提保证。 图12 干净飞机着陆轨线Fig.12 Landing trajectory of clean aircraft 图13 飞机着陆过程安全预警方法对比Fig.13 Comparison of safety warning methods during landing phase 图14所示为飞机结冰后(结冰因子取0.3),驾驶员根据不同的安全预警方法进行操纵应对所产成的不同着陆轨线。红色实线为飞机结冰后驾驶员不进行任何补偿操纵而形成的轨迹;绿色实线为飞机结冰后驾驶员根据传统的迎角限制进行操纵而形成的轨迹;蓝色实线为飞机结冰后驾驶员根据动力学限制安全预警方法进行操纵应对所形成的轨迹。另外根据2种安全预警方法进行的操纵应对方法是相同的,即:在保证飞机不超过安全限制的同时保证飞机速度不低于失速速度、不撞地且满足着陆要求,且在危险情况下通过操纵改飞机下滑过程为爬升或平飞过程,以便除冰后进行二次着陆。由于本文主要进行安全预警方法的优越性说明,故不进行二次着陆的相关仿真,因此结冰飞机改出过程的仿真停止于飞机脱离飞行风险或发生事故。另外图中蓝线和绿线为驾驶员操纵后,轨线形式出现率最高的情况,即:基于动力学限制进行改出操纵训练时也存在失败情况,但概率相对较低,同样基于传统的迎角限制进行改出训练时也存在成功的情况,同样概率也较低。 图14 基于不同安全预警方法的结冰飞机着陆轨迹Fig.14 Landing trajectories of icing aircraft based on different safety warning methods 通过训练和图14和图15可知,基于动力学限制的安全预警方法在此种情况下将提前于迎角限制方法约4.5 s进行危险告警(2.2节理论值为15.5 s,是因为驾驶员不进行任何补偿操纵所致,因为驾驶员进行补偿操纵必定在一定程度上提高飞行安全,也因此减少了2种方法的差异,另外该时间针对不同的飞行情况,此处给出具体时间仅为说明文中提出方法的优越性)。且通过大量改出操纵训练可知,在37.5 s进行结冰飞机的着陆改出的成功率(约90%)将明显高于在40~42 s进行结冰飞机的着陆改出操纵的成功率(约30%),且难度也明显降低,因此可在一定程度上说明基于动力学限制的安全预警方法进行飞行训练可提高结冰飞机的着陆飞行安全。 图15 结冰飞机安全预警值对比Fig.15 Comparison of safety warning for icing aircraft 本文基于微分流形理论确定了结冰飞机的动力学边界,并详细分析了结冰程度对边界的影响规律,在此基础上利用动力学边界的特性对飞行风险进行了量化,最后基于MATLAB/Simulink和Flightgear仿真平台搭建了飞行仿真训练系统,并对上述方法的优越性及可用性进行了验证。具体结论如下: 1) 将非线性稳定域作为飞机的动力学边界,该动力学边界可综合考虑飞机各状态之间的动力学耦合情况。研究了不同结冰情况下结冰飞机动力学边界的变化情况,结果表明,严重结冰导致动力学边界明显收缩,且耦合特性表现突出。 2) 利用动力学边界对飞行风险进行了量化,并在此基础上提出一种可考虑外界因素影响的动力学限制安全预警方法,该方法考虑了动力学的耦合特性,可提前于传统迎角限制预警方法进行飞行风险告警。 3) 将基于动力学边界的动力学限制安全预警方法应用于飞行仿真训练系统,并对结冰飞机的着陆飞行科目进行了仿真模拟训练,最终验证了该方法的可行性及相比于传统方法的优越性。1.2 干净飞机动力学边界确定及算法验证




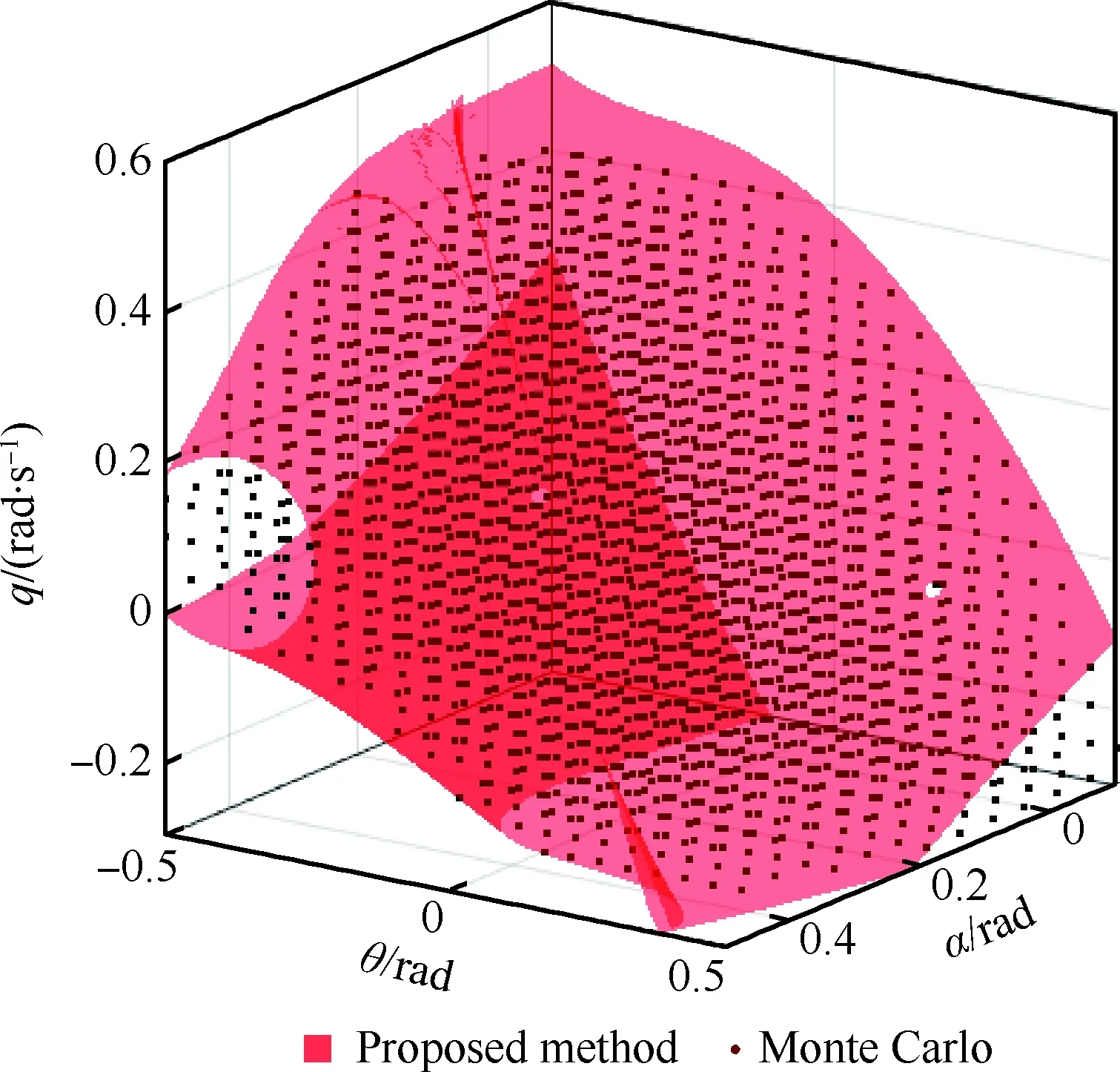

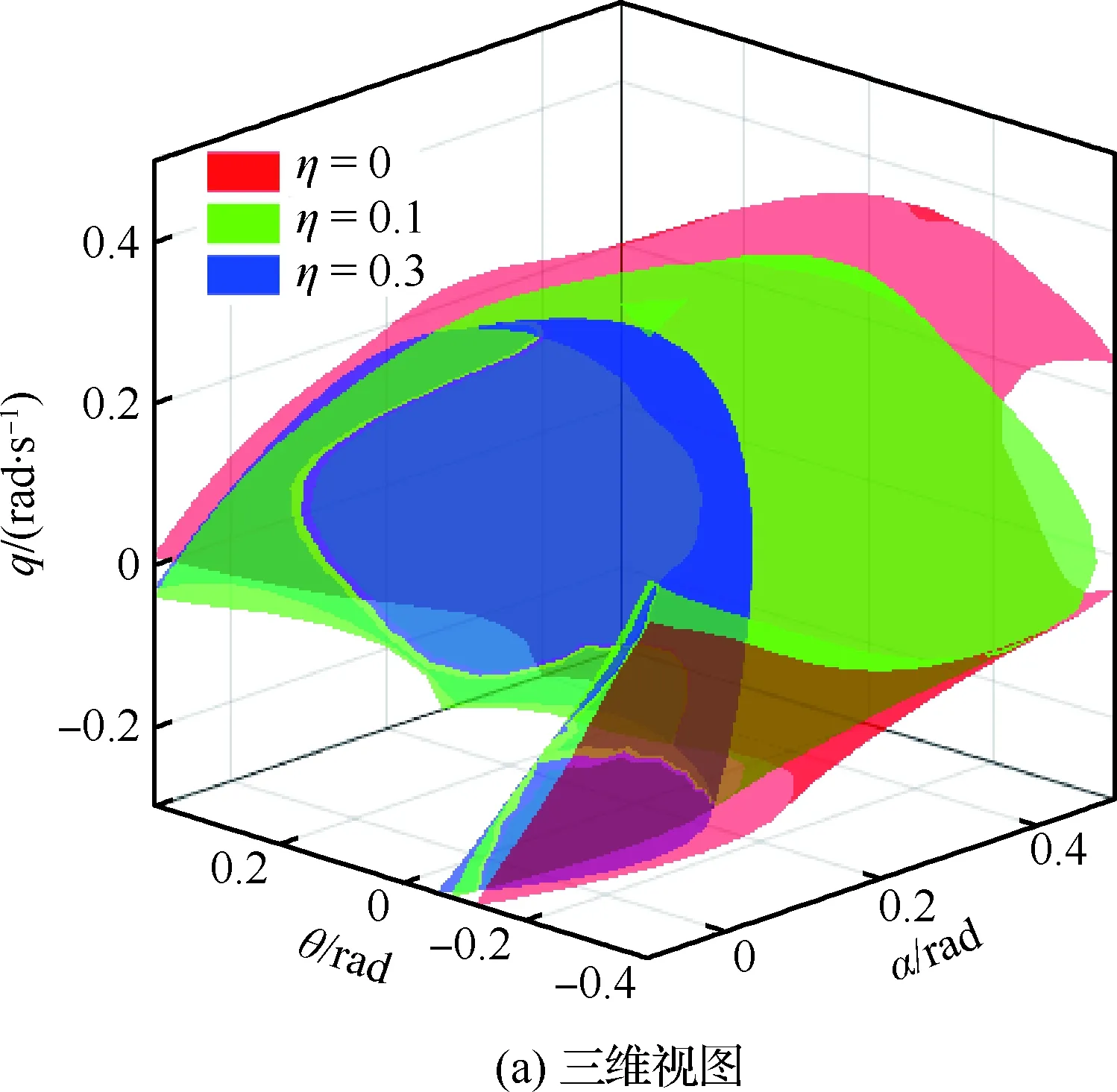
1.3 结冰飞机动力学边界确定

2 结冰飞机飞行安全预警方法
2.1 飞行风险评估及其量化方法

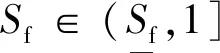
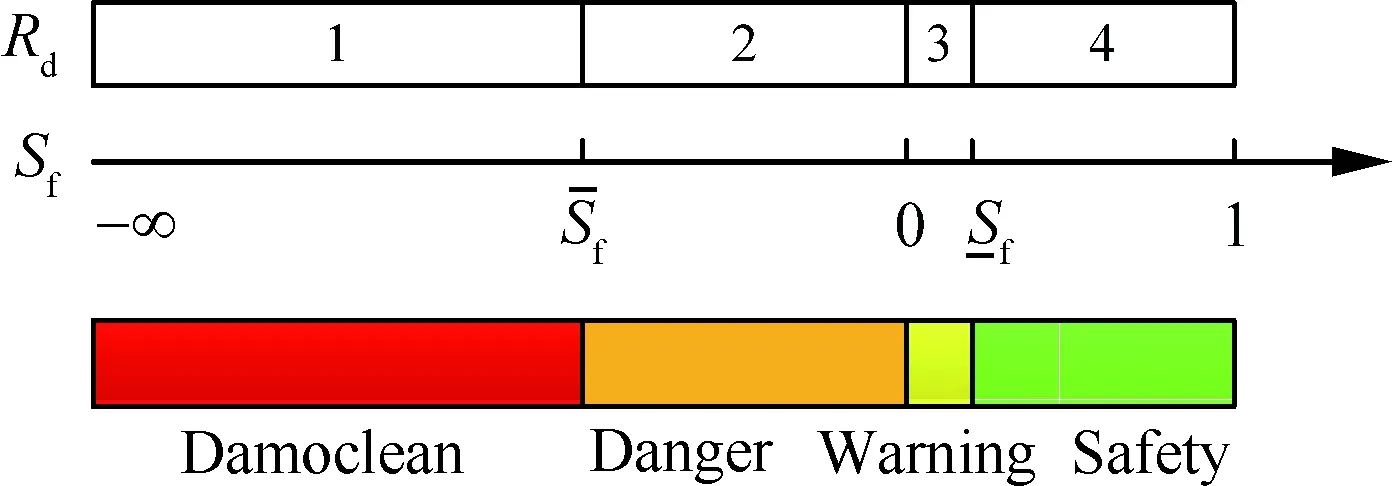
2.2 相对于传统边界预警方法的优越性


3 结冰飞机着陆下滑阶段飞行训练
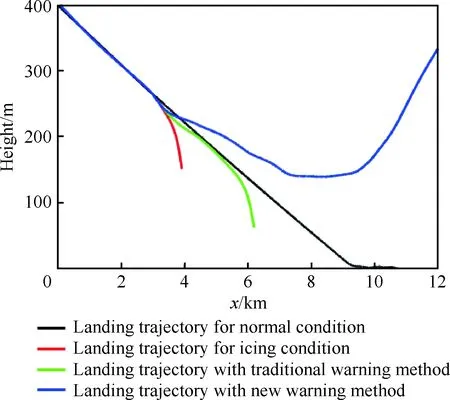
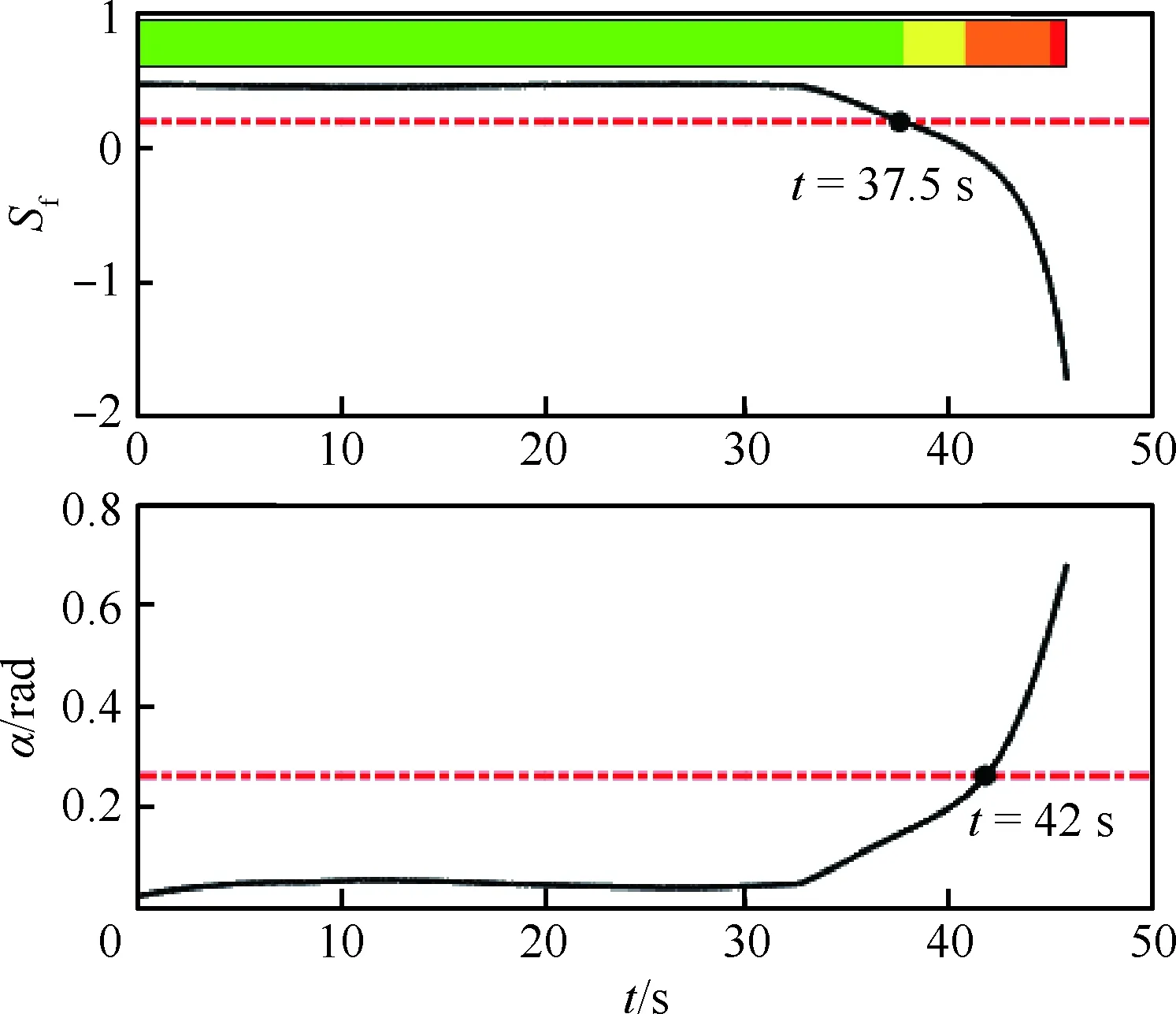
4 结 论

