阻拦索断裂对螺旋桨舰载机着舰安全影响数值分析
张声伟,段卓毅,耿建中,王立波
航空工业第一飞机设计研究院,西安 710089
起飞与着陆是陆基飞机飞行事故的多发阶段,舰载机着舰技术难度远大于陆基飞机,危险性也更高。国内外关于舰载机着舰技术方面的研究很多,研究内容涉及到舰载机着舰引导技术[1-3]、舰体运动对舰载机安全着舰的影响[4-5]、舰载机起降动力学研究[6-8]、机舰适配性研究[9]、舰载机着舰拦阻技术[10-12]和舰载机飞行品质规范[13]等多个方面。由于是小概率事件,关于阻拦索断裂对舰载机着舰安全影响研究的文献很少。但事实表明阻拦索断裂所导致的舰载机坠海事件并不少见,如俄军的SU-33、Mig-29K、美军的F-18等舰载机均发生过此类事故。阻拦索断裂瞬间释放的巨大动能会对甲板工作人员造成致命伤害,若事故飞机偏离着舰跑道冲入舰载机群,将引起连环爆炸,造成巨大损失。
2016年3月8日,美军艾森豪威尔号航母的一架E-2C舰载预警机在着舰滑跑时阻拦索断裂,该机飞离航母后航迹下沉,经6.3 s爬升至航母甲板高度。相对于喷气动力舰载机,螺旋桨动力舰载机推重比小,气动阻力大,不利于加速复飞。为解释螺旋桨动力舰载机逃逸复飞成功的原因,本文采用仿真技术,数值模拟了螺旋桨舰载机着舰、舰面滑跑与离舰复飞全过程主要运动参数的变化,并深入分析其动力学特性。
本文首先根据舰载机拦阻滑跑、阻拦索断裂滑跑与空中飞行3个阶段的动力学方程,分析其各阶段的运动特性,并建立了螺旋桨动力舰载机着舰复飞的仿真模型、拦阻索工作模型、发动机的动力响应模型、舵面操纵模型与螺旋桨动力舰载机着舰构型下的气动力动力影响修正模型[14]。再基于以上模型,数值模拟了阻拦索断裂情况下E-2C舰载机逃逸复飞过程,并对其航迹与主要运动参数进行了数值分析,得出其逃逸复飞成功的原因。最后变参数分析了影响螺旋桨动力舰载机复飞安全的敏感因素。
1 舰载机拦阻滑跑与复飞运动特性
阻拦索断裂情况下舰载机逃逸复飞的运动参数分析可分为拦阻滑跑、断裂滑跑与空中飞行3个阶段。飞机每个阶段的动力学方程、发动机工作状态、操纵指令与运动参数变化均不相同。
1.1 拦阻滑跑阶段运动分析
离舰速度是影响舰载机复飞安全的重要参数,其值取决于着舰速度、第I阶段的速度损失与第Ⅱ阶段的速度增量。第I阶段为急剧减速运动,动力学方程为
(1)
式中:ne、Te与φe分别为发动机数量、拉力、拉力与机身轴线夹角;Daer、Dzl与Fz分别为飞机气动阻力、阻拦索拉力与滑跑摩擦阻力;m、v与α为舰载机着舰质量、飞行速度与迎角。该阶段飞机速度损失主要取决于阻拦索断裂前所吸收的能量,较大的速度损失会影响舰载机复飞安全,因此有必要定量分析舰载机拦阻滑跑阶段的受力情况、速度与位置变化情况。
1.2 断裂滑跑阶段运动分析
第Ⅱ阶段飞机作加速运动,动力学方程为
(2)
速度增量主要与发动机的动力响应特性、气动阻力与剩余甲板长度有关。气动阻力计算需要考虑动力影响、侧滑及航向配平带来的阻力增量,侧滑角计算公式为
β=arctan(vcrsinθd/v)
(3)
式中:vcr为航母速度;θd为着舰跑道与航母舰体轴线的夹角。
1.3 空中飞行阶段运动分析
舰载机离舰后经历下沉、拉平与爬升3个阶段。飞机质心作非定常曲线加速运动,同时伴随着机体绕质心轴作俯仰转动。该阶段飞机的迎角、航迹角φ及其角速度ωφ、俯仰姿态角θ及其角速度q快速变化,飞机的动力学方程为
(4)
式中:qv为速压;S为飞机参考面积;ca为平均气动弦长;Iy为飞机俯仰惯性矩;CT为拉力系数;CL、CD和Cm分别为升力系数、阻力系数和俯仰力矩系数。
2 仿真模型
真实反映敏感因素对舰载机运动参数的影响,不追求细节一致是仿真模型建立的原则。
2.1 建立系统仿真模型
螺旋桨动力舰载机着舰复飞的运动仿真系统模型见图1。
图1表明:螺旋桨动力舰载机着舰复飞仿真系统主要由飞行控制系统模型、动力系统响应模型、阻拦索工作模型、气动力修正模型与飞机运动方程解算模块组成。
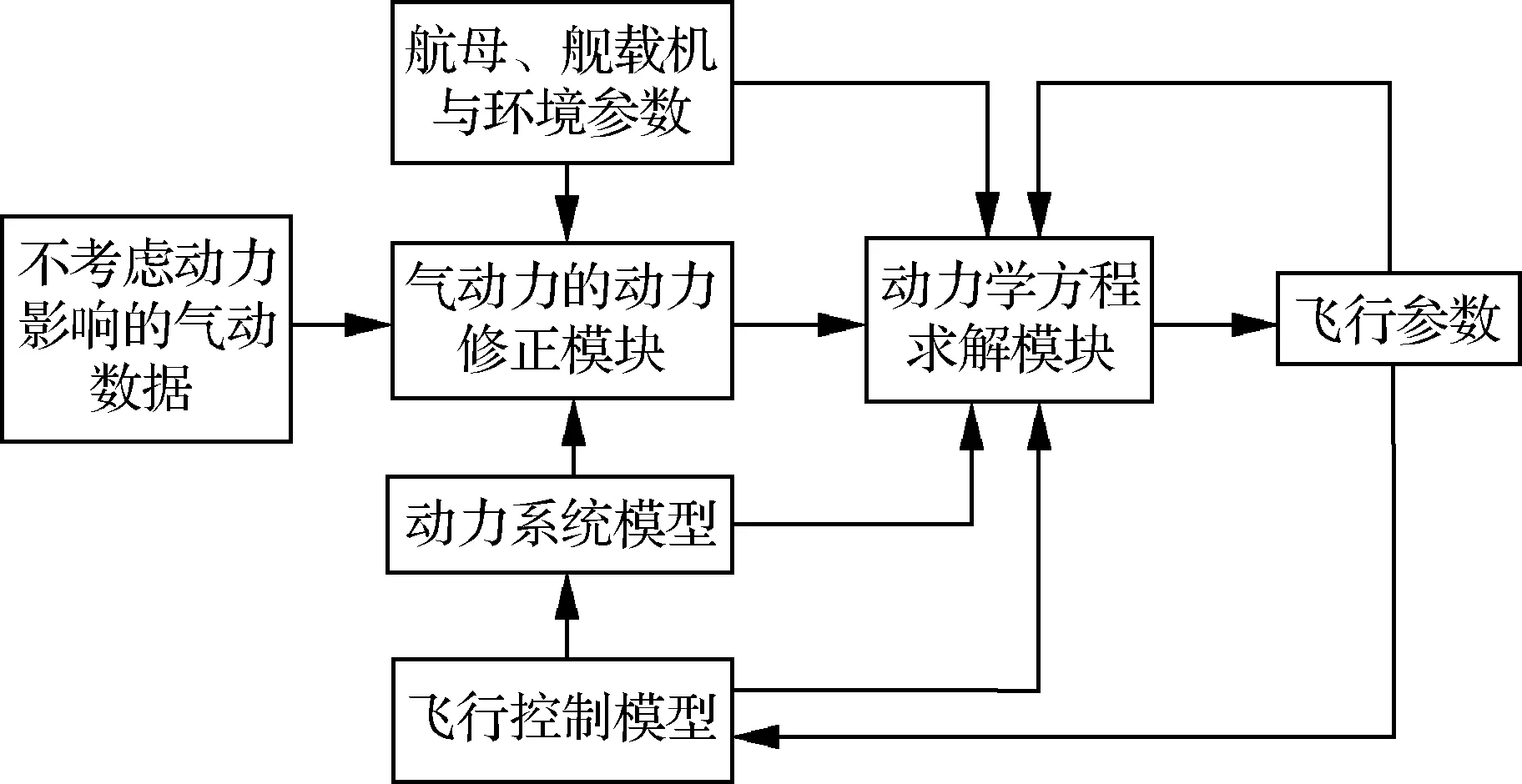
图1 螺旋桨舰载机着舰复飞仿真模型Fig.1 Simulation model of landing and re-flight of propeller carrier aircraft
2.2 气动力模型
舰面滑跑阶段的气动力计算公式为
(5)
式中:CLoff、CDoff与Cmoff分别为舰载机无动力状态下的升力、阻力与俯仰力矩系数;CLT、CDT与CmT分别为螺旋桨拉力产生的的升力、阻力与俯仰力矩系数增量;CLN、CDN与CmN分别为螺旋桨法向力产生的的升力、阻力与俯仰力矩系数增量;CLs、CDs与Cms分别为螺旋桨滑流产生的的升力、阻力与俯仰力矩系数增量。
空中飞行阶段的气动力计算公式为
(6)
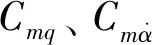
2.3 阻拦索工作模型
本文阻拦索受力的数学模型为
(7)
式中:E为舰载机着舰时的总能量;s为水平位移;smax为舰载机拦阻滑跑距离;η为阻拦装置的机械效率;f为摩擦力系数;p1为主液压缸活塞上的压力;A2为活塞等效面积,拦阻系统的液压缓冲装置比较复杂,其详细信息可参见文献[15-17]。
该模型不同于弯折波模型,其重点关注拦阻索受力与飞机位移的函数关系,而不是拉力的波动情况。
阻拦索强度损失的不确定性使舰载机拦阻滑跑的动能损失具有随机性,为模拟这种随机性,本文采用断裂系数(阻拦锁断裂时所受张力/阻拦索载荷峰值)用于仿真计算舰载机的动能损失。
2.4 油门操纵及其响应模型
舰载机着舰瞬间,飞行员将油门杆推到最大位置,若成功挂索,会将油门收到慢车位置,否则将继续保持最大油门,发动机拉力会持续增加。据美军标MIL-F-8785C要求,设发动机油门响应时间为2.5 s,飞行员操纵反应时间为0.3 s。发动机油门响应曲线参考相似涡桨发动机。
2.5 升降舵操纵约束
舰载机飞离甲板时,飞行员感觉到飞机下沉后开始拉杆,其反应时间设为0.3 s。升降舵操纵模型参见舰载机设计标准[18]对起飞过程中飞机运动参数的约束为:
1) 迎角不得大于90%CLmax所对应的迎角。
2) 航迹最低点的加速度不得小于0.07g。
3) 飞机的俯仰姿态角速度不得大于12 (°)/s。
根据以上约束,舰载机第Ⅲ阶段升降舵的控制律设计思想为:保证飞机迎角不大于12.8°,俯仰角速度不大于12 (°)/s。飞机纵向加速度不小于0.686 m/s2。
2.6 运动参数计算模型
1) 舰面滑跑阶段速度与时间计算模型:
(8)
式中:Δv为飞机速度损失量;vland、ve分别为该阶段的起始速度与终点速度;sz与tz分别为该阶段的滑跑距离与滑跑时间。
2) 离舰飞行阶段运动参数计算模型:
(9)
式中:Δh为飞机航迹相对于甲板的下沉量;s3z为水平飞行距离;t3z为空中飞行段的时间。
3 仿真计算与数据分析
数值模拟的对象为E-2C舰载机在艾森豪威尔号航母着舰逃逸复飞过程,目的在于揭示螺旋桨舰载机复飞轨迹、运动参数与其动力学特性。
3.1 仿真计算输入数据
艾森豪威尔号航母的几何参数:着舰跑道长度为238 m,与舰体轴线的夹角为8.5°。第1道阻拦索距舰尾50 m,每道阻拦索的间距为12 m,甲板距海平面高度为19.8 m。飞机着舰时航母运动速度取27 km/h,阻拦索断裂系数取0.86。
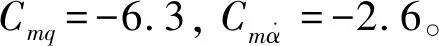
对象飞机的气动力计算采用模拟动力影响的CFD数值计算方法。E-2C构型数据来源于文献[19],建立的数字模型与真实飞机会有一定差别,但这种差别不会产生大的气动特性变化。
3.2 仿真计算
仿真数据显示:对象飞机甲板上滑跑的时间为3.8 s;飞离航母至爬升到航母甲板高度所用时间为6.2 s。对象飞机着舰复飞3个阶段的末端速度vend、水平位移量sx与所用时间见表1。
对象飞机第Ⅲ阶段的航迹下沉量与速度的变化曲线见图2。仿真计算显示:对象飞机空中段的初始速度为42 m/s,略小于其失速速度,但升降舵效率并未明显下降。飞机飞离甲板3.4 s,航迹达到最低点,航迹最大下沉量为10.2 m。飞机离舰6.2 s时爬升至甲板高度,速度增大到53.1 m/s。
视频显示E-2C着舰复飞的过程为:飞机于13∶55∶6拦阻钩挂索,在着舰跑道上滑跑3.9 s之后飞离航母,6.3 s后爬升至甲板高度。仿真数据与视频显示的时间比较吻合。
表1对象飞机着舰逃逸复飞3个阶段的运动参数
Table1Dynamicparametersofthreestagesoflandingandescapere-flightofobjectaircraft

StageTime/ssx/mvend /(m·s-1)Ⅰ1.360.837.4Ⅱ2.592.242Ⅲ6.2303.953.1
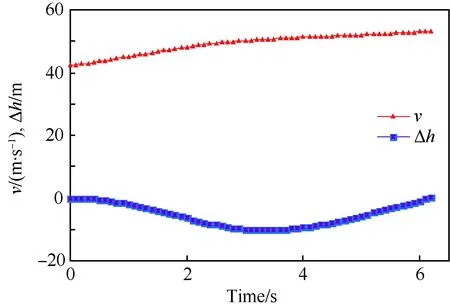
图2 飞机速度与航迹下沉量随时间变化Fig.2 Variation of aircraft’s velocity and track sinking value with time
3.3 仿真数据
对飞机各阶段主要运动参数变化与受力情况的分析,可得到对象飞机复飞成功的原因。
3.3.1 舰上滑跑阶段
仿真计算显示:第Ⅰ阶段舰载机速度从53.3 m/s急剧减小到37.1 m/s,加速度由0.6 m/s2迅速变化为-34.1 m/s2,舰上滑跑距离为60.8 m。第Ⅱ阶段平缓加速,离舰时速度增加到42.1 m/s,加速度增大到2.56 m/s2。该阶段舰载机的速度损失量为21.1%,速度与加速度变化见图3,阻拦索拉力变化见图4。
图4表明:挂索成功后,阻拦索拉力急速增大,经1.3 s达到其可承受最大拉力778 kN后断裂,阻拦索的拉力随时间非线性变化。图4曲线变化形态与美国军用标准MIL-STD-2066所示曲线相似。美军航母所用的MARK7-mod3阻拦系统最大行程94.5 m,阻拦索载荷峰值为911 kN,出现位置在最大拦阻行程的0.59~0.61处。
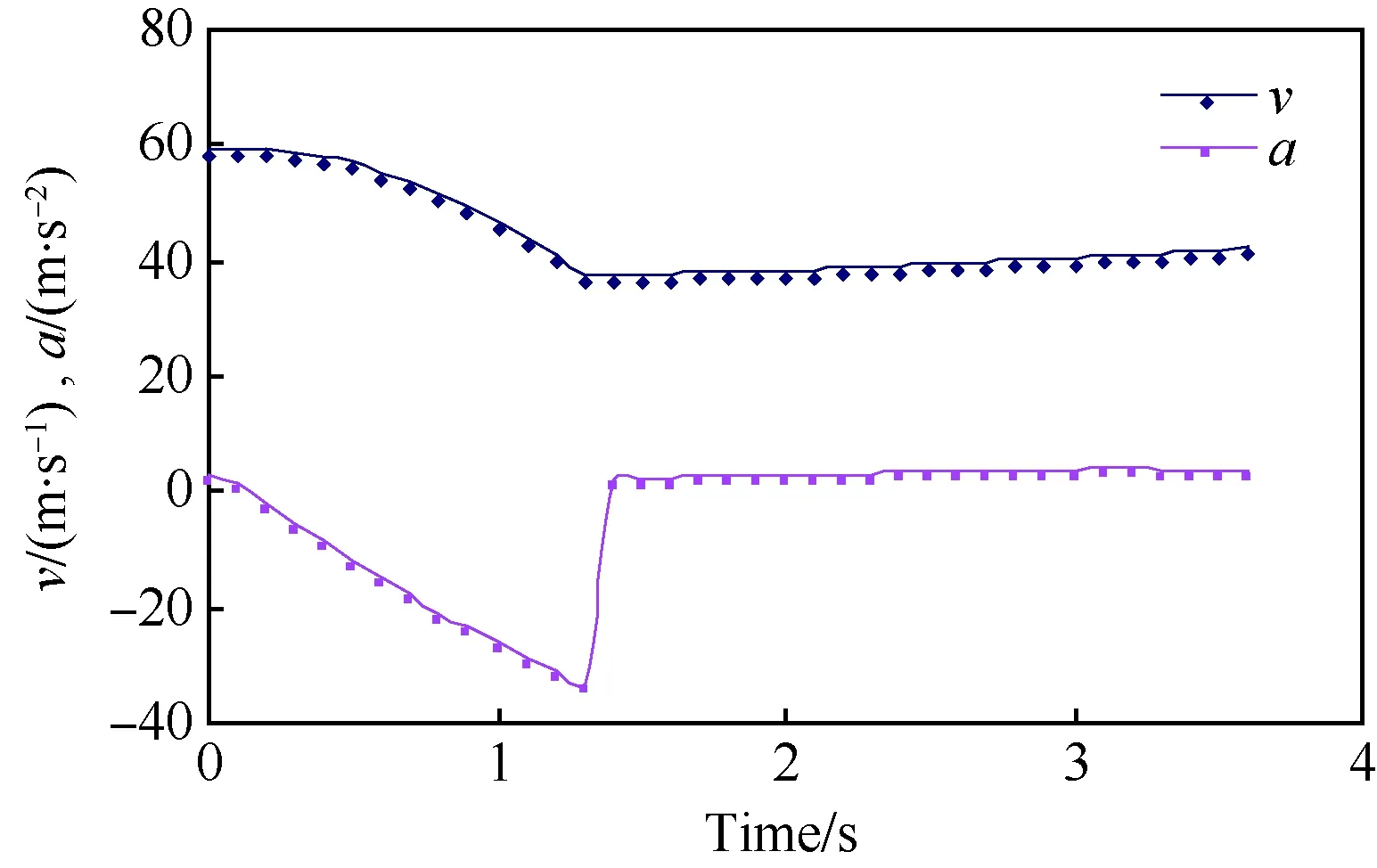
图3 前2个阶段飞机速度与加速度随时间变化Fig.3 Variation of v and a with time in the first two stages

图4 阻拦索拉力随时间变化Fig.4 Variation of drag of block cable with time
3.3.2 离舰飞行阶段
评判舰载机复飞安全的直接参数为航迹下沉量,减小航迹下沉量最直接的措施是增大舰载机航迹角速度。航迹角是俯仰姿态角与迎角之差,提高舰载机的俯仰操纵效能,增大俯仰角加速度是快速改变舰载机飞行航迹的关键措施。
分析舰载机航迹角的变化,必须考虑飞机俯仰姿态角与迎角的变化。对象飞机第Ⅲ阶段的航迹角、俯仰姿态角、迎角与升降舵偏转角变化曲线见图5,航迹角速度、俯仰角速度、迎角变化率与升降舵偏转角变化曲线见图6。
图5和图6显示:对象飞机离舰2.3 s时俯仰姿态角速度达到最大值9.1(°)/s, 3.0 s时迎角达到最大值12.5°,迎角与俯仰角速度最大值均符合设计标准的要求。飞机离舰3.5 s时航迹角由负值变为正值,航迹由下沉改为爬升。由于飞机的惯性与气动阻尼所致,对象飞机俯仰姿态角、航迹角与迎角的变化滞后于升降舵偏角的变化。
由第Ⅲ阶段舰载机的动力学方程可知,舰载机俯仰姿态角与航迹角的变化主要取决于其静态俯仰力矩特性,气动阻尼特性、升降舵操纵效率与俯仰惯性矩。对象飞机的静态俯仰力矩系数Cmwz、气动阻尼产生的俯仰力矩系数Cmzn、飞机动态俯仰力矩系数Cmz与升降舵偏转产生的俯仰力矩系数Cmδe变化见图7。

图5 舵偏角、俯仰角、航迹角与迎角随时间变化Fig.5 Variation of δe,θ,φ and α with time
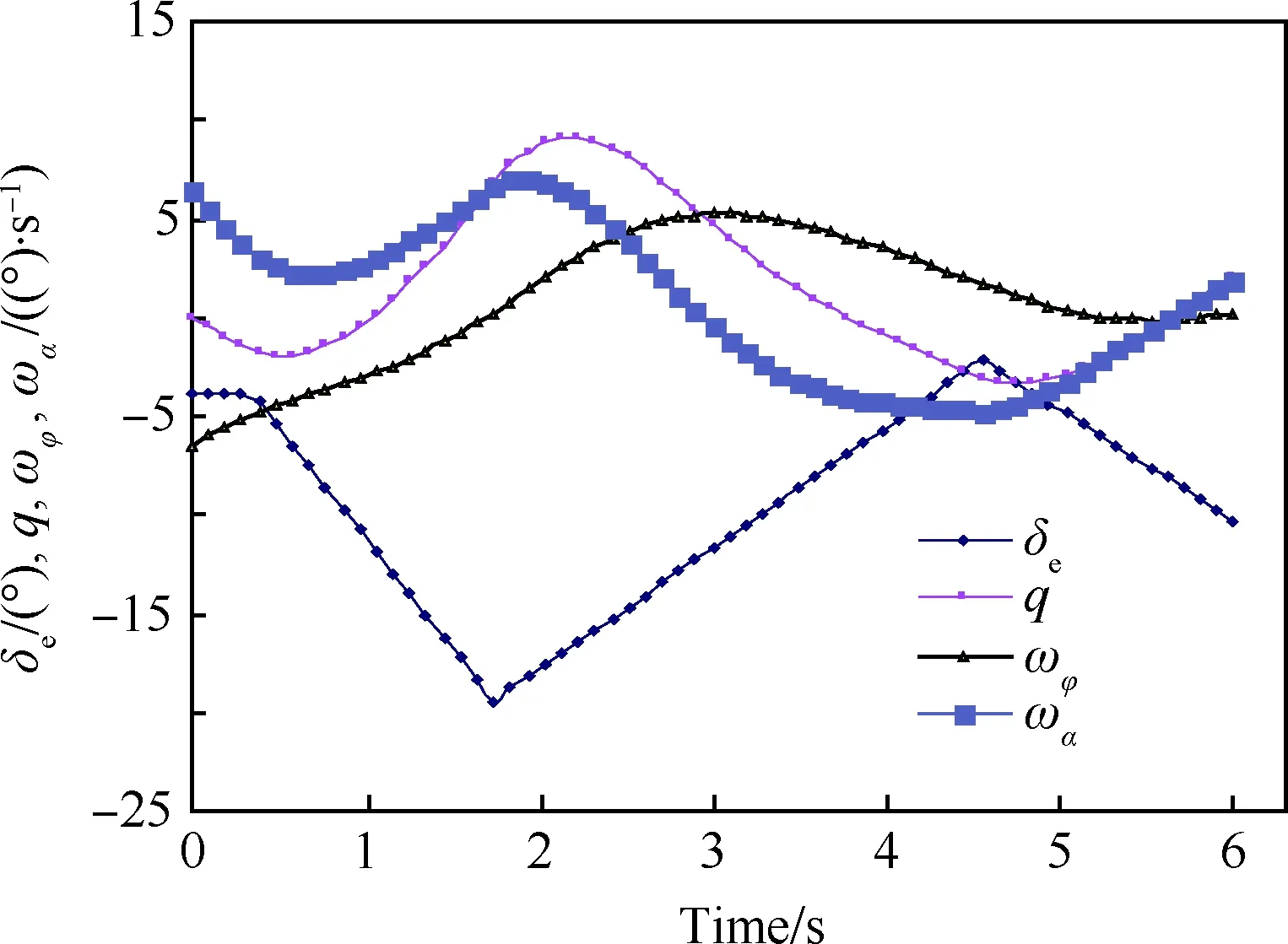
图6 舵偏角、俯仰角速度、航迹角速度与迎角变化率随时间变化Fig.6 Variation of δe,q,ωφ and ωα with time
图7中曲线说明对象飞机的静态俯仰力矩系数在-0.1~-0.2之间变化,下俯力矩较小。由于升降舵的快速偏转,由飞机俯仰角速度与洗流时差效应所产生的气动阻尼力矩系数较大,且变化剧烈。对象飞机的动态俯仰力矩系数大部分时间在-0.07~0.06之间变化。升降舵最大偏角产生的上仰操纵力矩系数为0.35,大部分时间内可提供较大的上仰力矩。对象飞机俯仰力矩特性与升降舵操纵性能,为迅速改变飞机航迹提供了足够的上仰驱动力矩。
离舰速度的减小会明显降低喷气动力舰载机的升降舵操纵效率。螺旋桨动力飞机的滑流一方面会改善飞机失速特性并减小其纵向静稳定性,另一方面使平尾处速压增大,提升升降舵的操纵效率。螺旋桨动力舰载机可保证小速度下其升降舵的操纵效率不会明显下降。
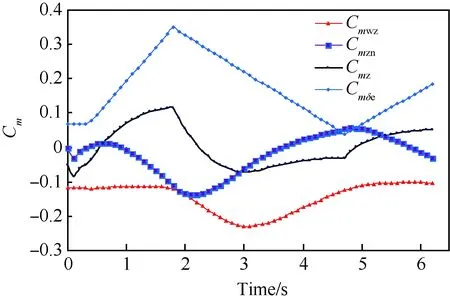
图7 飞机俯仰力矩与操纵力矩系数随时间变化Fig.7 Variation of aircraft’s Cmwz, Cmzn, Cmz and Cmδe with time
4 敏感因素分析
理论分析表明:舰载机的气动特性、动力特性、离舰速度与飞行员的操纵技术均会对舰载机航迹改变产生较大影响。但各因素对航迹下沉量的影响与敏感性需通过仿真计算获得。
4.1 气动特性影响
动力对螺旋桨飞机气动特性影响的仿真计算比较复杂,相关方法可参见文献[20]。仿真计算表明:螺旋桨动力舰载机着舰构型的气动特性受动力影响明显,其中动力对升力与俯仰力矩特性的影响最为显著。图8~图10为对象飞机着舰构型无动力状态与不同拉力系数状态下的升力系数、阻力系数与俯仰力矩系数曲线的对比。
对象飞机的纵向气动特征参数对比见表2。表中数据显示螺旋桨的动力增升效应明显:对象飞机在拉力系数为0.4时的最大升力系数CLmax与升力线斜率CLα分别比无动力状态下增加了39%与29.7%。螺旋桨舰载机一般为低速运输机或预警机,低翼载与大展弦比直机翼气动布局使飞机具有良好的升力特性与较小的失速速度。动力增升效应进一步提高了飞机的升力线斜率与最大升力系数。飞机航迹改变的速率直接取决于升力的增量与增速,螺旋桨舰载机着舰构型的升力线斜率约为小展弦比舰载战斗机的2.6倍,因此其航迹改变能力远高于喷气动力战斗机。
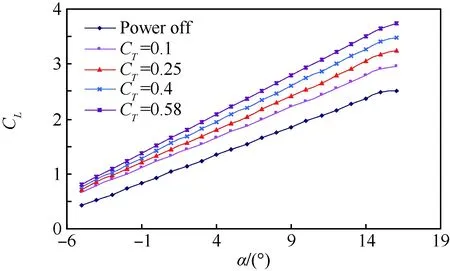
图8 螺旋桨动力对升力系数的影响Fig.8 Effect of propeller power on CL

图9 螺旋桨动力对阻力系数的影响Fig.9 Effect of propeller power on CD
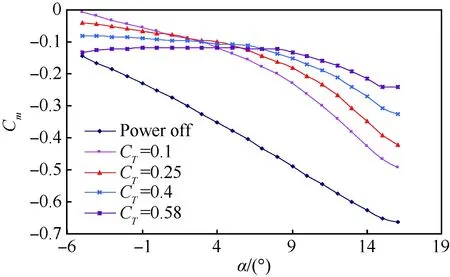
图10 螺旋桨动力对俯仰力矩系数的影响Fig.10 Effect of propeller power on Cm
表2 对象飞机的气动特征参数Table 2 Aerodynamics parameter of objects aircraft

CTCLαCLmaxCD0CMα0CmCLOff0.1012.50.1211-0.252-0.250.10.1192.950.2112-0.067-0.1440.250.123.230.1955-0.072-0.0850.40.1313.480.2582-0.091-0.0360.580.1413.730.2582-0.118-0.003
动力对螺旋桨舰载机俯仰力矩特性的影响最为显著,对改变飞机航迹的影响也最直接。受动力影响的对象飞机俯仰力矩曲线整体上移,拉力系数为0.4时0°迎角的俯仰力矩系数Cmα0与纵向静稳定性CmCL仅为无动力状态的35.7%与14.4%(-1°~8°迎角区间)。螺旋桨飞机气动特性的动力影响来源于桨盘法向力、螺旋桨滑流与拉力。与外吹式襟翼动力增升技术[21]不同,喷气式襟翼会使飞机的下俯力矩增加,而螺旋桨的法向力与滑流对平尾的下洗作用会显著增大飞机的上仰力矩,并减小飞机的纵向静稳定性,可显著改善飞机操纵的敏捷性。
动力影响也有不利的一面,对象飞机在拉力系数为0.4时零升阻力系数CD0达到了0.258 2,比无动力状态增大了113%,不利于飞机加速。
为说明气动特性变化对螺旋桨舰载机逃逸复飞航迹下沉的影响,本文采用对象飞机无动力状态下的气动力数据进行了仿真计算。带动力与无动力2种状态下对象飞机的航迹下沉量与俯仰姿态角速度曲线见图11与图12。
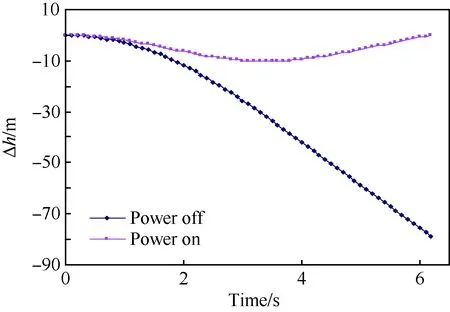
图11 2套气动数据模拟的航迹下沉量对比Fig.11 Comparison of values of Δh between two sets of aerodynamic data simulation
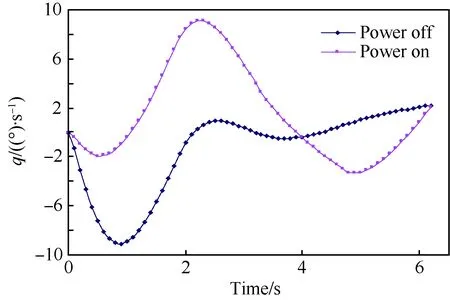
图12 2套气动数据模拟的俯仰姿态角速度对比Fig.12 Comparison of values of q of two sets of aerodynamic data simulation
图11和图12表明:未经动力修正状态下飞机的最大俯仰角速度只能达到2.1 (°)/s,远小于动力修正状态的9.1 (°)/s,舵面操纵能力太差,因此无动力状态下飞机航迹角负值一直在增大,离舰6.2 s后其航迹下沉量达到81 m。
4.2 离舰速度影响
离舰速度取决于舰载机着舰速度与阻拦索断裂系数。算例中着舰速度为1.25Vs,阻拦索断裂系数取0.86,离舰速度计算值为0.99Vs。当断裂系数系数取0.93或着舰速度减小至1.2Vs,离舰速度计算值为0.91Vs。2个离舰速度舰载机的航迹下沉量变化曲线见图13。

图13 不同离舰速度的航迹下沉量对比Fig.13 Comparisons of track sinking value at different approach velocities
图13显示:0.91Vs离舰速度,对象飞机的航迹下沉量增大到15.2 m,爬升到甲板高度的时间增大到9.4 s,分别比0.99Vs离舰速度的航迹下沉量与爬升时间增大50%与52%。
4.3 操纵指令影响
推拉杆的转换时间与操纵速率对舰载机复飞的运动参数产生较大的影响。图14为bz、lv与hv这3种操纵方式对应的升降舵偏角变化曲线。bz为仿真计算所使用的升降舵操纵方式。lv方式相对bz方式将推杆速度减小46%。hv方式相对bz方式,推杆与拉杆速度均增大25%。
bz操纵方式:对象飞机离舰之后,飞行员以13 (°)/s的速度快速拉杆,迅速改变飞机的姿态角。当升降舵偏角达到最大值,以7.2 (°)/s的速度推杆,防止飞机迎角与姿态角速度超过设计标准的约束值。当迎角反馈值小于7°,再以6.8 (°)/s的速度拉杆,增大升降舵偏角,以防止飞机迎角过小所导致的机翼气流分离。
对象飞机3种操纵方式的航迹下沉量、迎角与俯仰角速度变化曲线见图15~图17。
图15~图17曲线显示:lv操纵方式由于升降舵偏角长时间处于大偏角,致使迎角超过对象飞机的最大使用值。hv操纵方式操纵速率增大,需经多次调整升降舵偏转方向,方可保证舰载机迎角与俯仰角速度不超出约束值,航迹下沉量相对bz方式减小0.71 m,但爬升时间增加了26%。
通过优化操纵策略,可减小舰载机的航迹下沉量,并保证逃逸复飞操纵的安全。
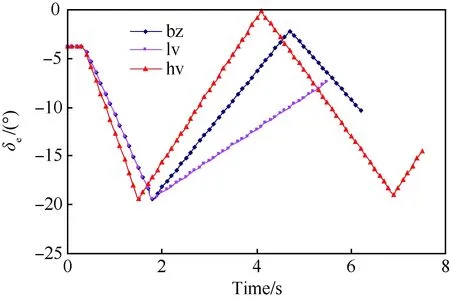
图14 3种操纵方式升降舵偏角-时间曲线对比Fig.14 Comparison of curves of δe and time in three models
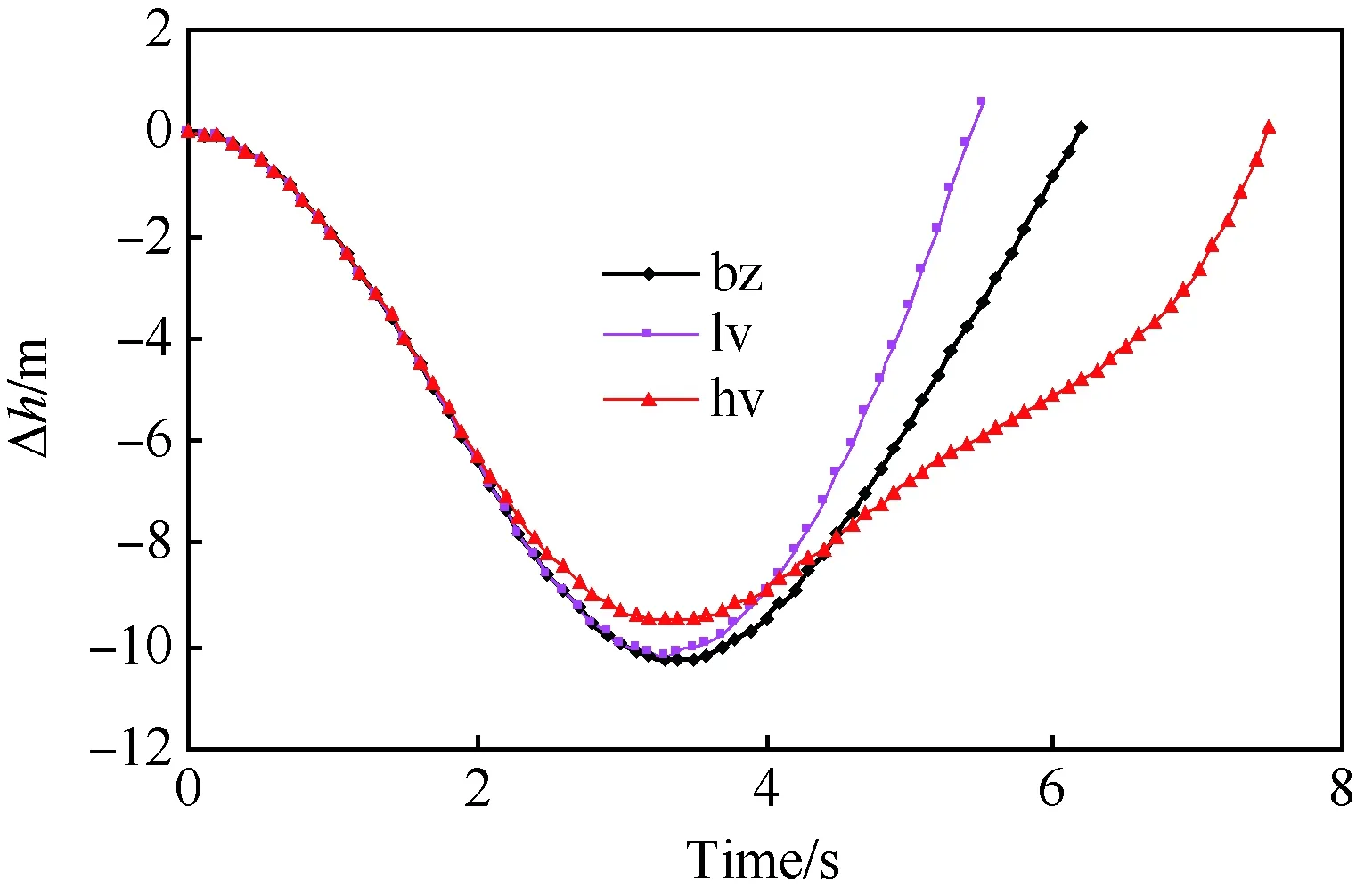
图15 3种操纵方式航迹下沉量-时间曲线对比Fig.15 Comparison of curves of track sinking value and time in three models

图16 3种操纵方式迎角-时间曲线对比Fig.16 Comparison of curves of α and time in three models

图17 3种操纵方式俯仰角速度-时间曲线对比Fig.17 Comparison of curves of q and time in three models
5 结 论
1) 螺旋桨舰载机动力影响产生的气动特性变化,有利于快速改变飞机航迹角,是影响其复飞安全的关键因素。
2) 螺旋桨滑流对平尾的下洗与桨盘法向力使飞机俯仰力矩曲线显著上移,8°迎角以下的纵向静稳定度减小85%,大大提高了飞机操纵的敏捷性。
3) 螺旋桨飞机特有的动力增升效应,使对象飞机的升力线斜率增大29.7%,最大升力系数增大39%,提升了升力对航迹角改变的贡献,并改善了失速特性。
4) 螺旋桨滑流增大了平尾处的速压与下洗,一方面保证了升降舵小速度下的操纵效率,另一方面提供了额外的上仰力矩。
5) 螺旋桨动力舰载机低翼载、大展弦比直机翼气动布局,具有良好的升力特性与较小的失速速度,是安全复飞的基础。

