舰载机机身加筋壁板屈曲疲劳试验

张彦军，朱亮，杨卫平，李小鹏，雷晓欣

航空工业第一飞机设计研究院 强度设计研究所，西安 710089

舰载机在弹射起飞和拦阻着舰的过程中，相邻扩散区机身壁板在弹射和拦阻载荷作用下反复失稳(进入张力场)，失稳的屈曲波在机身壁板上产生附加应力，从而降低结构的疲劳强度和改变疲劳破坏部位[1]。舰载机起降过程过载大，应力水平高，对机身结构设计要求高[2-3]。屈曲疲劳是结构在承受载荷达到一定水平(临界值)，进入反复失稳状态(弹性或塑性)后，由于承受交变载荷而发生破损断裂[4]。机身加筋壁板结构因结构效率高而广泛应用于航空航天领域，当壁板结构受到循环剪切载荷作用时便会出现屈曲问题与疲劳问题的耦合，即结构会在反复进入后屈曲状态的情况下发生疲劳破坏，或者是在产生一定的疲劳累积损伤后发生屈曲失稳或后屈曲破坏。

国内外对加筋板的屈曲问题开展了很多研究，当前很多学者主要研究结构在静态剪切载荷下的破坏[5]、屈曲后的应力分析[6]、压剪耦合下的屈曲和后屈曲失效行为[7]、复合材料加筋板的屈曲特性[8-9]。Wittenberg和Baten[10]研究了Glare材料的加筋结构剪切屈曲行为，Davila等[11]开展了循环载荷下后屈曲过程中模态改变的研究。

Lahuerta等[12]研究了风机叶片后缘复合材料的静力和疲劳屈曲失效,Tripathi等[13]研究了复合材料加强支柱轴向受压下，考虑屈曲的低周疲劳行为。张铁军等[14]研究了复合材料加筋壁板的损伤演化、屈曲行为及破坏模式。兑红娜等[15]通过建立了飞机某关键部位的结构载荷回归模型来进行寿命预测。陈勇等[16]研究了玻璃纤维增强铝合金层板高速冲击损伤容限特性。齐红宇[17]研究了发动机机匣用T300复合材料的屈曲疲劳累积损伤模型薛景川等[4]开展了屈曲疲劳的初步试验研究并与细节疲劳额定值(Detail Fatigue Rating， DFR)方法相结合。肖浩等[18]采用损伤力学方法初步考虑了薄板的后屈曲与疲劳损伤的耦合作用。Sedlack等[19]研究了超声速飞机在热力耦合极端环境下的屈曲疲劳行为。目前对机身加筋板反复屈曲的疲劳特性研究很少，也未用于飞机设计中结构参数的确定。

本文以张力场梁屈曲疲劳试验为基础，采用应变电测法和数字散斑(Digital Image Correlation, DIC)方法开展了临界屈曲载荷测试，并通过反复屈曲疲劳试验给出了2种不同厚度下的无量纲载荷比-寿命曲线及载荷比-张力场系数曲线。通过在机身加筋壁板设计阶段，同步考虑机体寿命指标，在满足疲劳要求的同时，给出控制结构进入张力场的程度即张力场系数，从而实现结构的轻量化设计。

1 机身加筋壁板受剪承载特点

机身加筋壁板受剪情况下，从载荷作用开始承载到最终破坏过程可分为3个主要阶段[4,20]。

第1阶段(失稳前)：剪切载荷较小，腹板所受的剪应力小于其临界屈曲剪应力(τ<τcr)，腹板内的拉应力与压应力大小相等，方向相互垂直，拉应力与加强筋条成45°倾角。

第2阶段(后屈曲状态)：随着剪切载荷的增加，腹板所受剪应力超过其临界剪应力(τ>τcr)，腹板已发生屈曲失稳，压应力将不再增加，保持常数。拉应力随着载荷增加而不断增加，形成一条张力场带，在四周框架中产生附加应力，由张力场以及加强筋与缘条组成的新结构来继续承受载荷。只要加强筋与缘条有足够刚度，张力场便可以逐步扩大，直到张力场内的应力达到腹板材料的屈服应力。

第3阶段(极限状态)：当腹板张力场内的应力达到材料屈服应力后，张力场充分扩展，最后在加强筋上出现塑性铰，使结构变为可变结构而发生破坏。

2 屈曲疲劳试验设计

2.1 试 件

机身壁板屈曲疲劳的试验研究采用张力场梁试件，用以模拟机身壁板、框、长桁等结构形式。本试件采用对称设计，以避免试验中试件的不对称破坏，试件结构示意图如图1所示。

图1 机身壁板屈曲疲劳试件结构示意图Fig.1 Sketch of specimen for fuselage structure buckling fatigue test

试件共2组，采用2种腹板厚度：t=1.2，1.5 mm，分别有12件和14件。2组试件除腹板厚度不同外，其他零件相同，支柱间距为280 mm，试件总体尺寸为1 200 mm×400 mm。

试件正反面对称。梁缘条为L型角材(50 mm×50 mm×5 mm)，背靠背用双排紧固件与腹板连接；腹板两侧支柱在加载处及两端为T型加筋(60 mm×40 mm×6 mm)，通过双排紧固件与腹板连接。其余均为L型型材(25 mm×25 mm×2.5 mm)加筋，通过单排紧固件与腹板连接。支柱与梁缘条重合部位采用支柱下陷方式与梁缘条连接。试件腹板材料为2A12-T4，支柱及凸缘均采用7050-T7451机械加工而成。

2.2 试验实施方案

试验采用下横梁两端支撑、上表面中间下压的三点弯曲加载方式，如图2所示，令腹板区域在剪切循环载荷下反复屈曲，从而产生疲劳损伤。

为防止过度面外弯曲位移，设计防弯约束装置，包含限位系统的试验夹具如图2所示。

图2 张力场梁屈曲试件三点弯曲加载示意图Fig.2 Sketch of three-point bending load of specimen for tension field spar buckling test

3 屈曲试验

3.1 试验内容

3.1.1 试验测量准备

本试验包括2个腹板考核区域如图1所示。在试件的左侧腹板考核区域粘贴应变片进行应变测量，应变片布置如图3所示，在试件左侧腹板正反2面对称粘贴应变花，在该段所属梁缘条和立柱腹板上粘贴成对单向片。

在右侧腹板考核区域采用非接触的DIC方法测量腹板位移应变分布，在腹板单面用白色和黑色油漆交替喷涂，制造白底黑点的随机人工散斑。安装非接触式光学应变测量系统进行测量。已喷涂数字散斑(Digital Speckle)的试件安装示意图如图4所示。

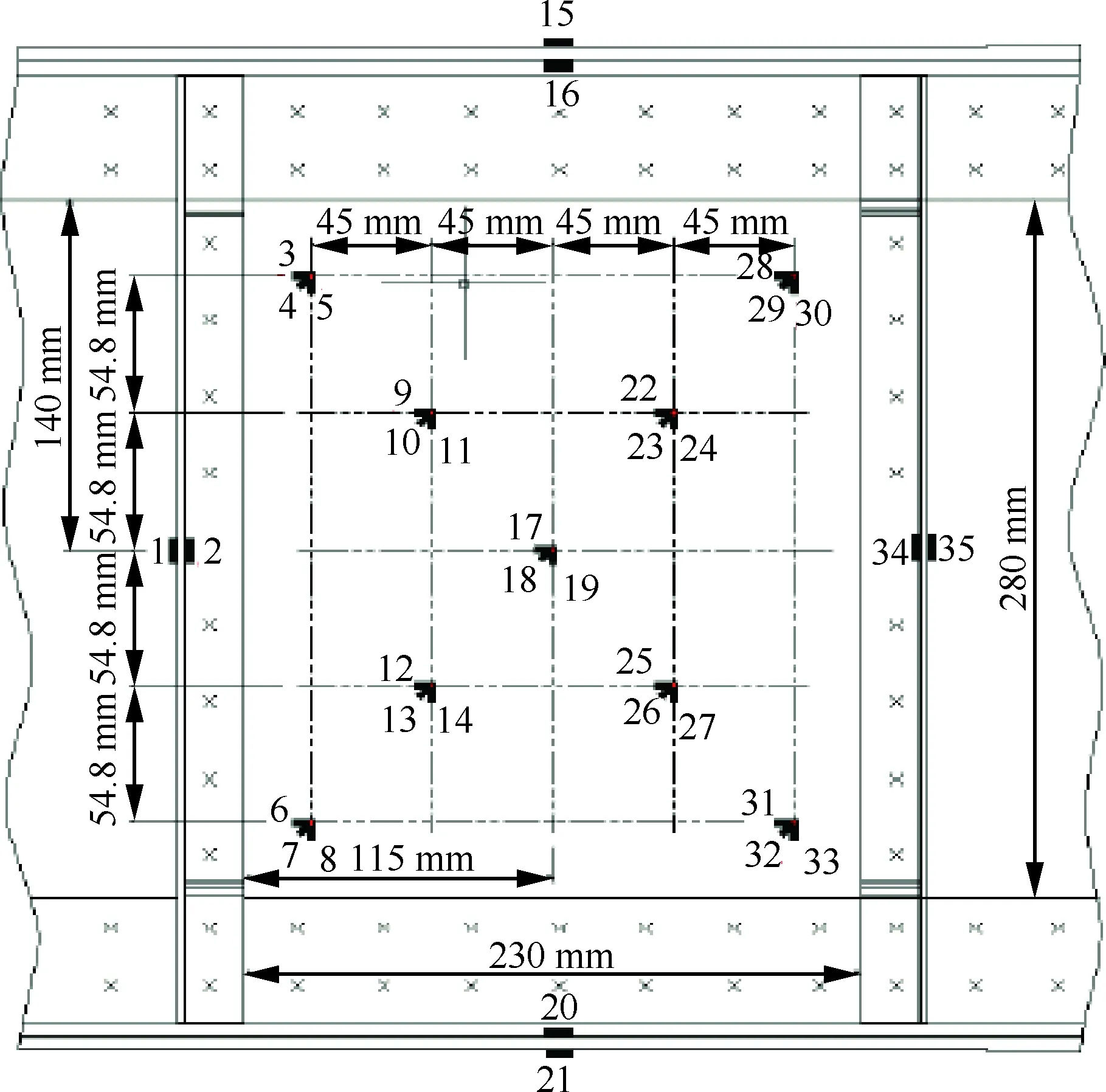
图3 试件应变片布置Fig.3 Strain gage arrangement of specimen

图4 试件安装示意图Fig.4 Test setup of specimen

3.1.2 试验项目

试验包括静力试验和疲劳试验2部分。静力和疲劳均需进行临界屈曲载荷测试，具体操作如下：

1) 每组试件各取1件先进行临界屈曲载荷测试，然后进行静力破坏试验。根据静力破坏试验结果，确定实际疲劳试验载荷。

2) 每组剩余所有试件均在完成临界屈曲载荷测试后，进行反复屈曲(张力场)疲劳试验。

3.2 试验结果

3.2.1 临界屈曲载荷测试

所有试件均进行屈曲临界载荷测试。按每级载荷增量小于0.5 kN逐级加载，每级载荷保载3～5 s，采集应变并拍摄散斑图。密切监控腹板2面应变变化，当腹板2面对应的应变值发生明显偏离时开始卸载。

由于实际应变曲线的分离是逐渐发生的，主观因素对分离点的判断影响很大，有时甚至很难作出适当的判断。为了辅助判断屈曲点，构造局部弯曲程度的量化指标(简称为弯曲度)，即

(1)

式中：εf和εb分别为前后表面对称布置的一对应变片测量的应变值。

根据应变曲线计算并绘出弯曲度随施加载荷的变化曲线，以18#应变片为例，给出腹板正反2面应变和弯曲度随载荷变化曲线，如图5所示。当弯曲度发生较明显偏折时，可能意味着2条应变曲线分叉开始，据此可确定临界屈曲点。

以厚度t=1.2 mm试件为例，给出数字散斑的非接触测量获得的离面位移结果。图6和图7分别给出腹板2条对角截面的离面位移云图和5个特定点位置的离面位移云图(加载历程0—18—0 kN)。图6中黑色对角截面近似垂直于张力场方向，沿该截面的离面位移分布反映出屈曲变形的皱褶模式。

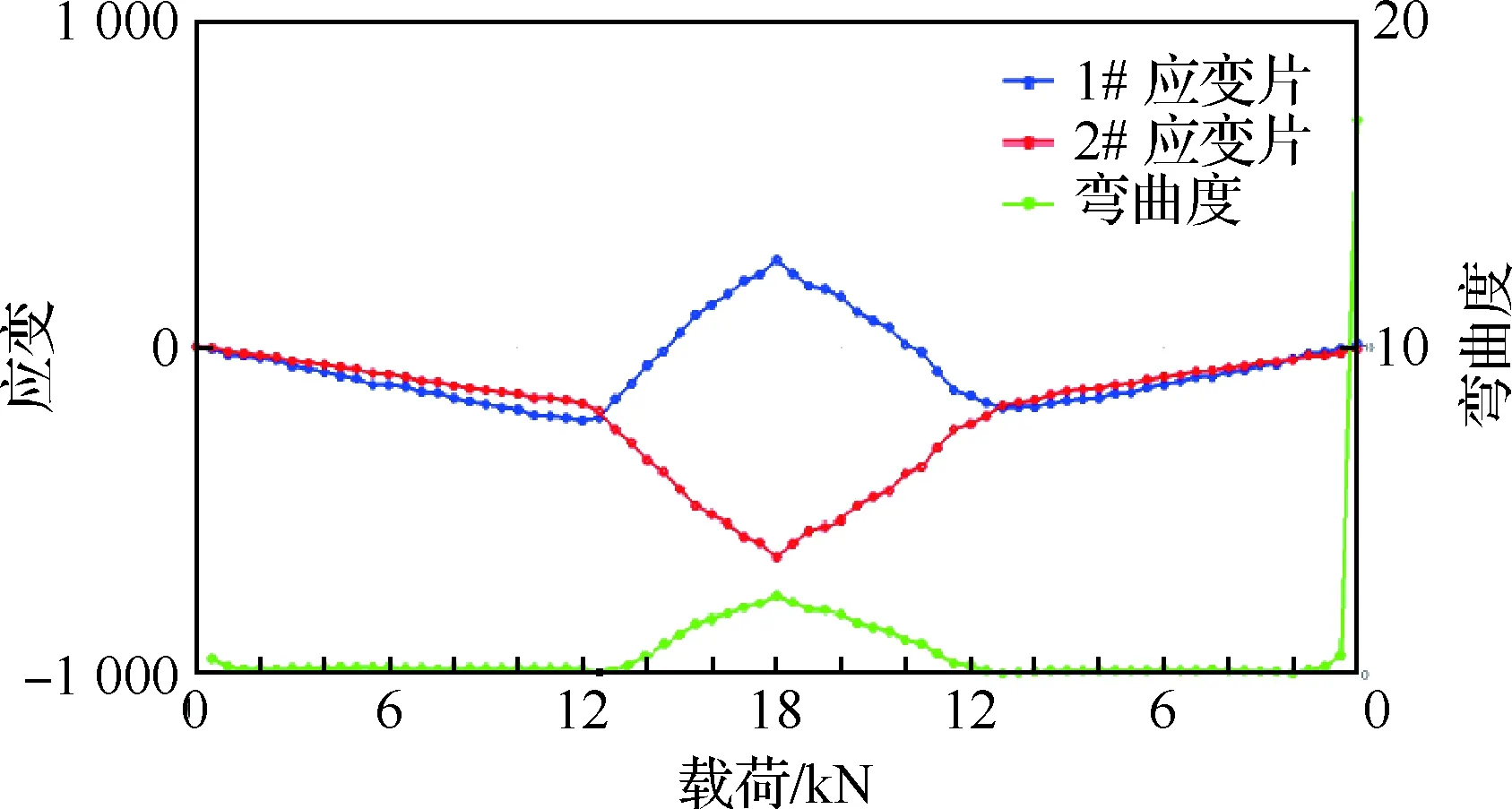
图5 18号测点处载荷-应变和弯曲度曲线(t=1.2 mm)Fig.5 Load vs strain and straightness curves at 18# measure point (t=1.2 mm)

图6 腹板对角截面离面位移(载荷18 kN,t=1.2 mm)Fig.6 Off-plane displacement of web diagonal sections (load=18 kN, t=1.2 mm)

数字散斑方法能够测量腹板面内位移、面内应变和离面位移分布，但由于不是双面应变测量，并不能依据双面对称位置应变曲线分叉规律估计临界屈曲点。

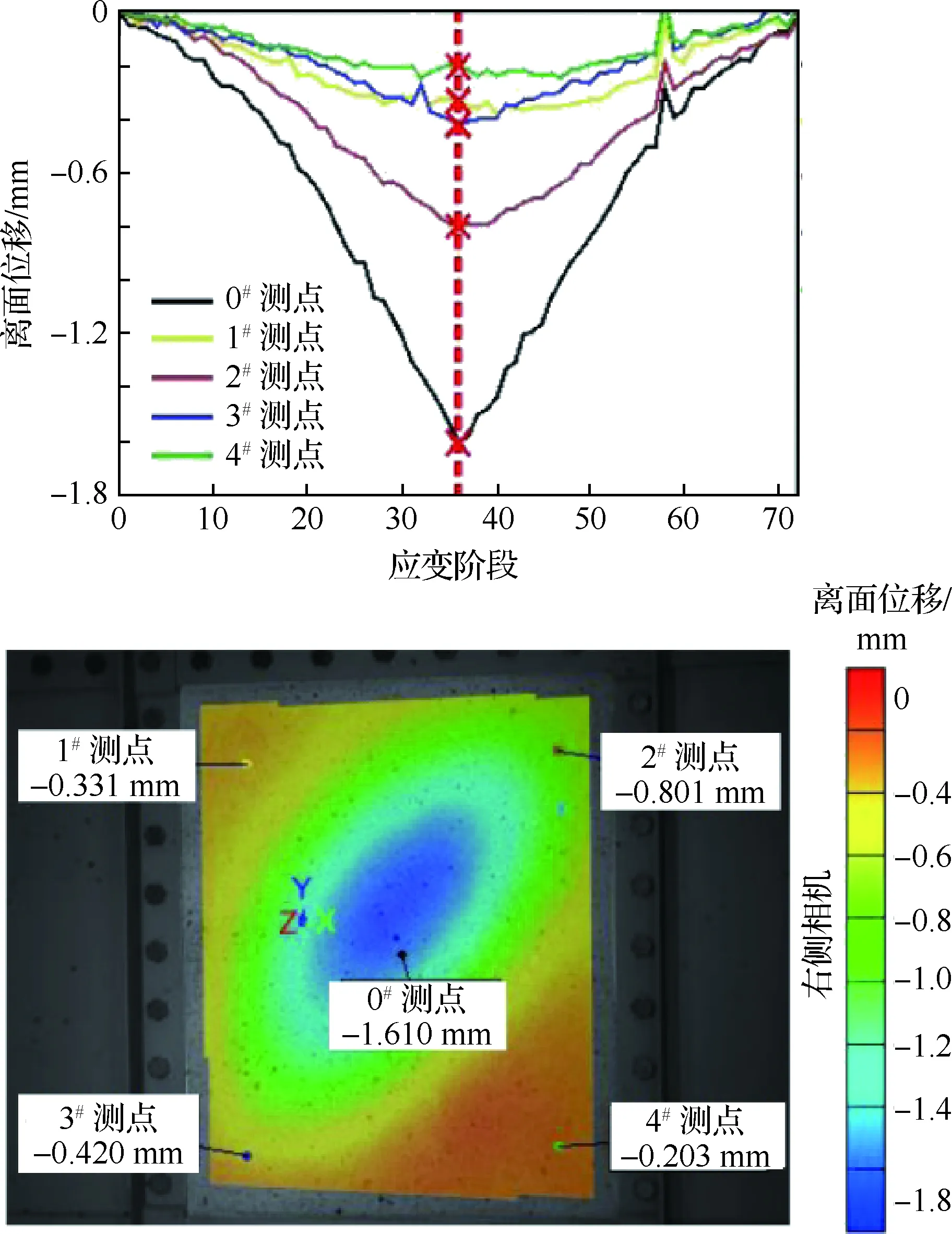
图7 各测点离面位移(载荷18 kN, t=1.2 mm)Fig.7 Off-plane displacement of test points (load=18 kN, t=1.2 mm)

因此，基于应变片电测法确定屈曲点仍然是较为可靠实用的测试手段。

测试给出t=1.2 mm试件(9件数据有效)、t=1.5 mm试件(14件数据有效)的临界屈曲载荷，其中部分试件测得有效结果只有1次、部分试件测得有效结果有5次。汇总结果分别如图8和图9所示。

对图8和图9中试验临界屈曲载荷分别求均值，得到t=1.2,1.5 mm试件的临界屈曲载荷Pcr均值分别为12.5、21.2 kN。通过试验可得出：

1) 对于同一试件，考核腹板内不同位置进入屈曲的时间有差异，表现出特定屈曲历程。

2) 同一厚度试件组内，不同试件的屈曲历程略有不同。

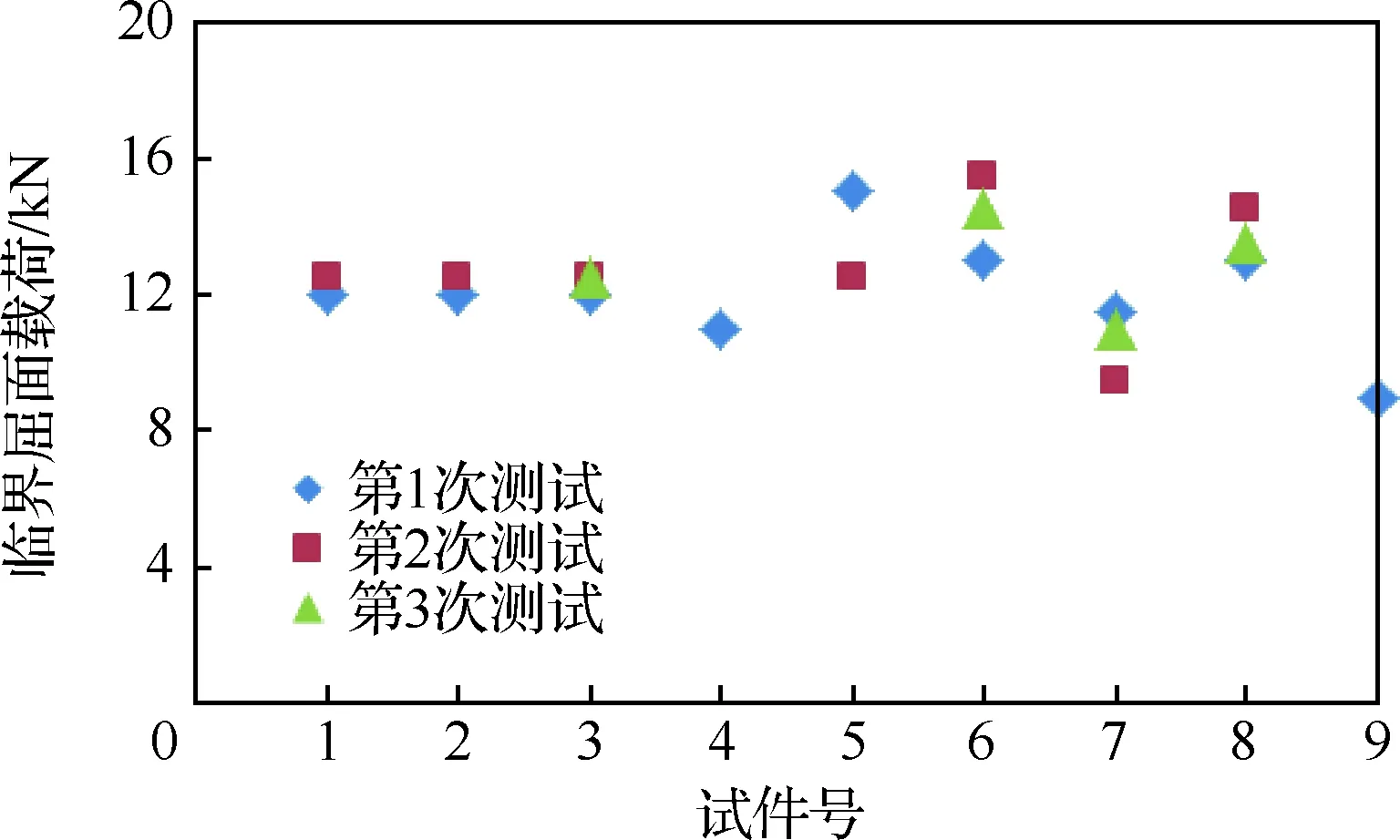
图8 t=1.2 mm试件临界屈曲载荷Fig.8 Critical buckling load of specimens (t=1.2 mm)

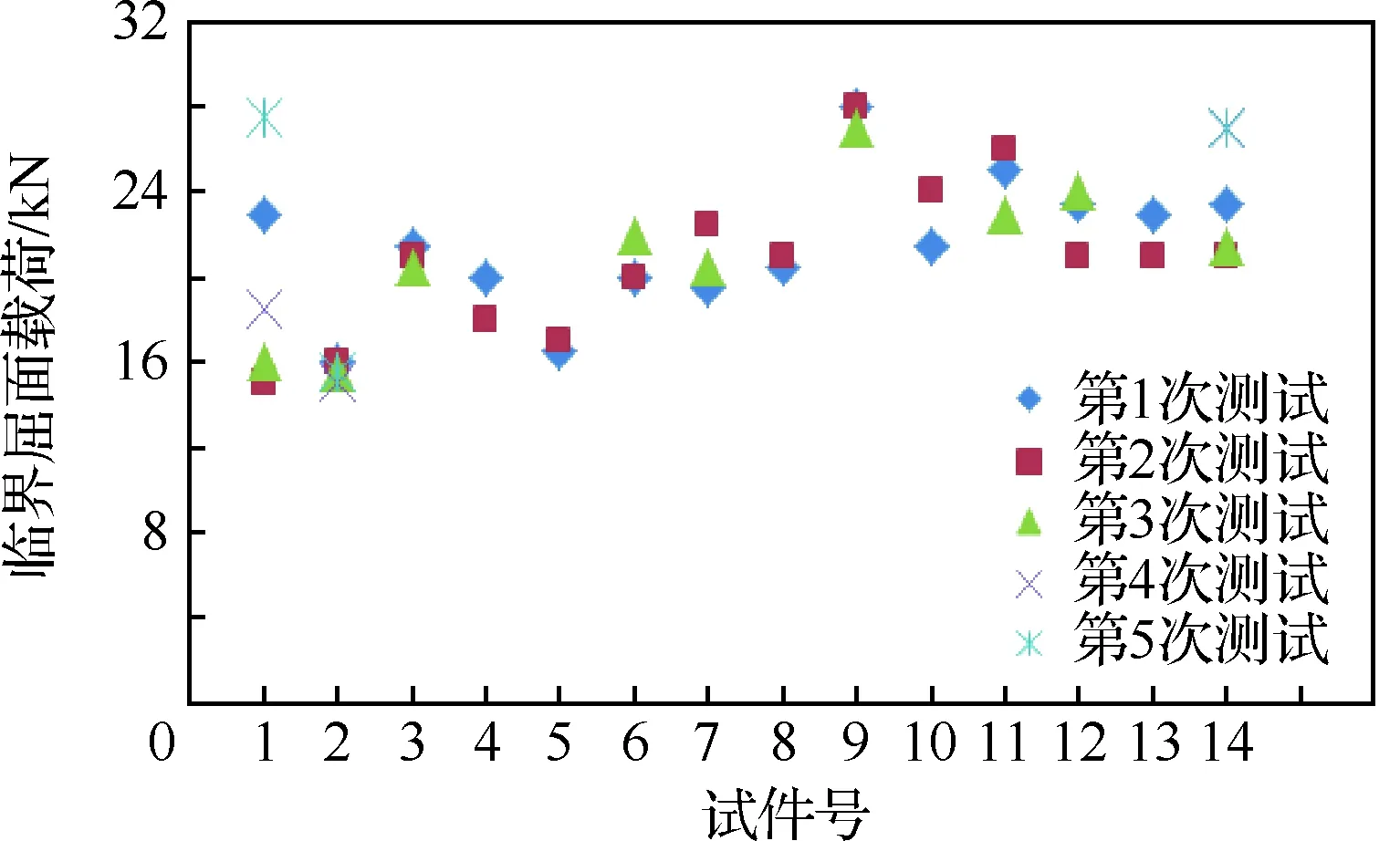
图9 t=1.5 mm试件临界屈曲载荷Fig.9 Critical buckling load of specimens (t=1.5 mm)

3) 同一厚度试件组内，不同试件临界屈曲载荷分散性较大。

上述第2)条和第3)条特点表明了飞机加筋壁板结构的复杂性，屈曲载荷和屈曲历程的分散性很大程度上来源于试件制造和试验实施过程中的差异，如三点弯曲压头加载和支点平面的平整度、平行度和加载的对称性等。

3.2.2 试件静力破坏情况

2组试件静力破坏载荷分别为241 kN和276 kN，破坏形貌如图10所示。从图10中可清楚地观察到腹板上形成的后屈曲张力场变形形貌，试件断裂起始于腹板左侧考核区的左上角。2组不同厚度试件的断裂形貌基本一致。

图10 试件静力破坏形貌Fig.10 Failure feature of static test of specimen

3.2.3 疲劳试验结果

根据静力试验及调试结果，每组各进行3级载荷水平下的疲劳试验，每级载荷水平下保证至少3个有效数据。疲劳试验应力比R=0.1，频率为3 Hz。部分试件疲劳开裂示意图如图11所示。试验结果表明，不同试件开裂模式及位置相近，裂纹基本出现在考核区受拉角上缘条边缘和外侧立柱缘条边缘腹板处。

对2组不同厚度的试件进行疲劳试验后，将外载荷P无量纲化为其与临界屈曲载荷Pcr的比值，即P/Pcr，给出疲劳试验结果如表1所示，表中:N为疲劳寿命；Nlm为对数中值寿命。

图11 试件开裂模式Fig.11 Crack mode of specimens

表1 屈曲疲劳试验结果Table 1 Results of buckling fatigue test

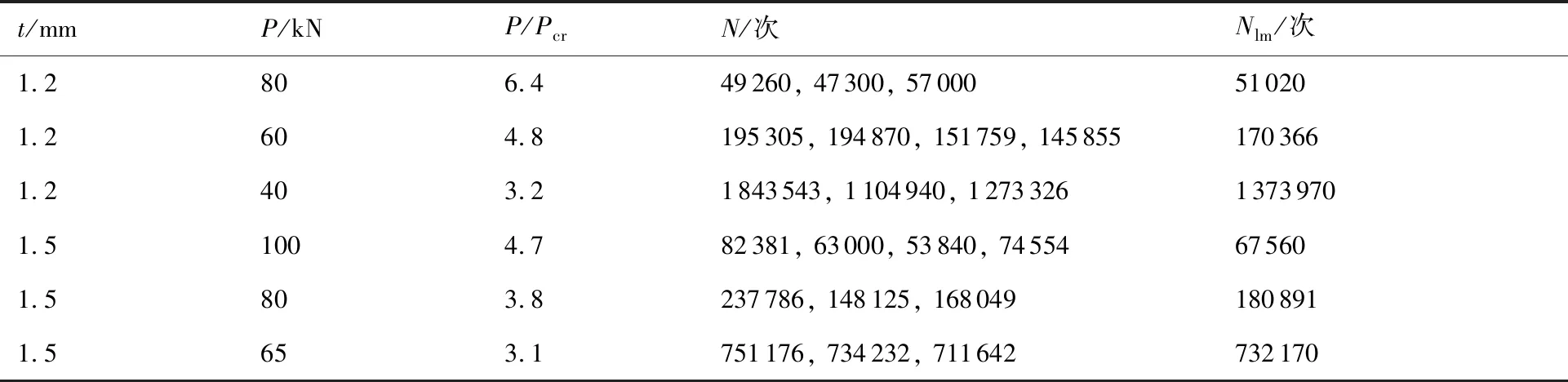
t/mmP/kNP/PcrN/次Nlm/次1.2806.449260, 47300, 57000510201.2604.8195305, 194870, 151759, 1458551703661.2403.21843543, 1104940, 127332613739701.51004.782381, 63000, 53840, 74554675601.5803.8237786, 148125, 1680491808911.5653.1751176, 734232, 711642732170

根据试验结果，绘制外载荷与临界屈曲载荷的比值和寿命关系曲线分别如图12和图13所示。

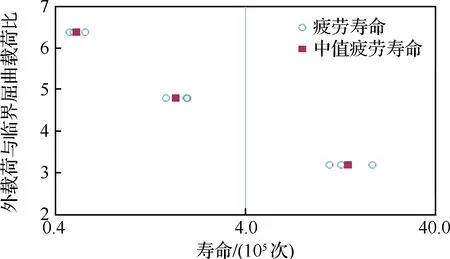
图12 外载荷与临界屈曲载荷比值-寿命曲线 (t=1.2 mm，R=0.1)Fig.12 Curves of ratio of load to critical buckling load vs life (t=1.2 mm, R=0.1)

图13 外载荷与临界屈曲载荷比值-寿命曲线(t=1.5 mm，R=0.1)Fig.13 Curves of ratio of load to critical buckling load vs life (t=1.5 mm, R=0.1)

4 计算分析

4.1 张力场理论下的屈曲载荷计算

飞机结构中通常采用的是不完全张力场(其设计载荷为临界值的几倍至几十倍)。普遍采用半经验的工程方法进行应力和强度计算。按照不完全张力场计算方法，弹性支持矩形平板的临界剪应力为[21]

(2)

式中：KSS为屈曲系数，取自图14[21]；E为弹性模量，取E=72 GPa；hc和Lc分别为支柱间和凸缘间的净距离；Rh和RL分别为支柱和凸缘的边界支持系数，取自图15[21]。图15中：t、tu、tfl分别为腹板、支柱、凸缘的厚度，对本文中2组试件，其值分别为1.2、2.5、5.0 mm和1.5、2.5、5.0 mm。

根据本文试件结构参数，由图14查得屈曲系数、由图15查得边界约束系数，并代入式(2)计算可得到对应的失稳临界剪应力，如表2所示。

将根据工程张力场理论计算得到的临界剪应力按式(3)表示为试件的临界外载荷Pcr，即

Pcr=2τcrthc

(3)

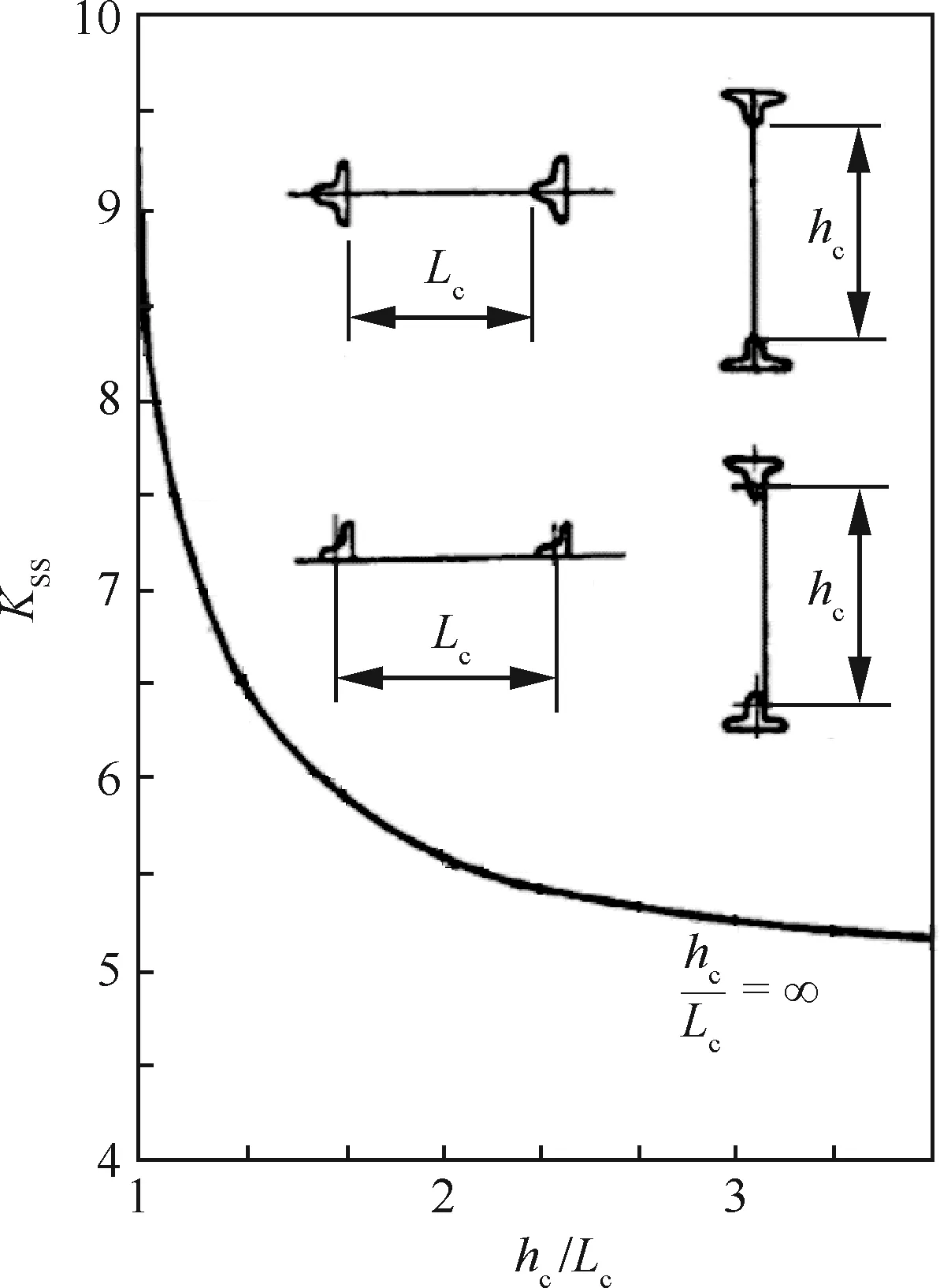
图14 屈曲系数曲线[21]Fig.14 Curve of buckling factor[21]

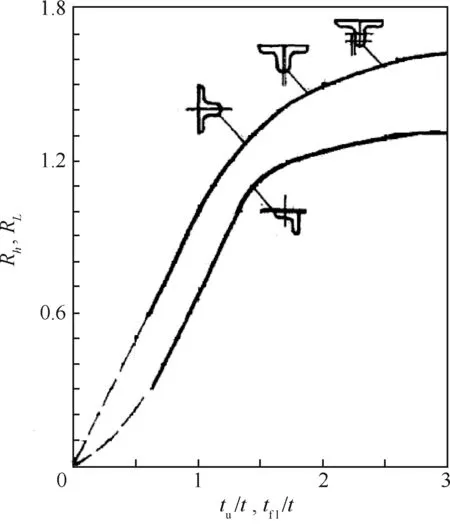
图15 边界约束系数曲线[21]Fig.15 Curves of boundary constraint factor[21]

与文中试验测得的临界失稳载荷对比如表3所示。

试验得到的t=1.2, 1.5 mm试件的临界屈曲载荷均值分别为12.5、21.2 kN，工程张力场的理论临界屈曲载荷(Pcr)与试验值相比，误差分别为4.8%、-0.5%。由此可见试验临界屈曲载荷与工程张力场理论得到的屈曲载荷吻合很好，表明工程张力场理论预测加筋壁板临界屈曲载荷有较高的精度。

表2试件对应的参数及临界剪应力

Table2Parametersandcriticalshearstresscorrespondingtospecimens

t/mmhc/mmLc/ mmKSStu/t1.22803536.812.081.52803536.811.67t/mmtfl/tRhRLτcr/MPa1.24.171.631.5314.011.53.331.631.3720.18

表3屈曲载荷的工程计算结果和试验结果对比

Table3Comparisonbetweenengineeringcalculatedresultsandmeasuredvaluesofbucklingload

t/mmPcr/kN计算结果试验结果1.211.912.51.521.321.2

4.2 张力场系数与寿命关系

在不完全张力场计算的工程方法中，把腹板中的总剪应力τ分成2部分：一部分由剪力场τs承受；其余部分由完全张力场τdt承受。

(4)

式中：K为张力场系数。

张力场系数K是加筋壁板进入张力场程度的描述。该系数是结构在设计发图过程中极为关心的一个参数，允许进入张力场程度高，则可以减少结构材料，有效降低结构重量。

根据文献[21]，张力场系数K取决于外载荷和结构的失稳临界载荷，并可通过式(5)计算得到：

(5)

式中：φ=(τ-τcr)/(τ+τcr)，τcr由表3中试验测得的临界屈曲载荷计算得出。

计算不同载荷水平下的张力场系数，并绘制P/Pcr与张力场系数关系曲线，如图16所示。

设某舰载机设计寿命为12 000次起落，以拦阻扩散区结构为例，每次起落按拦阻一次计算，取分散系数为4。设机身壁板厚度为1.2 mm，可由图12的载荷与寿命关系曲线查得外载荷P为80.5 kN，P/Pcr=6.4，再由图16可查得相应的张力场系数为0.21，即在结构设计中，为保证满足设计目标寿命的疲劳要求，应在结构静力分析时控制张力场系数不超过0.21。

因此，在结构设计初期将飞机寿命指标纳入加筋壁板张力场设计，通过合理控制张力场程度可有效实现结构的轻量化设计。

值得注意的是，目前仅使用工作载荷与临界初始屈曲载荷的比值作为结构设计中张力场控制的依据，后续还需进一步考虑其他参数影响，如紧固件尺寸及排数、加筋壁板的框距与桁距比等。

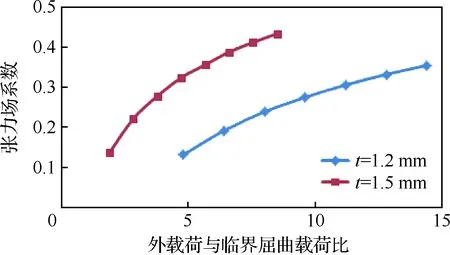
图16 张力场系数与载荷的关系Fig.16 Variation of tension field factor with load

5 结 论

1) 工程张力场理论预测机身加筋壁板的临界屈曲载荷与试验实测值吻合很好。应变电测法判断临界屈曲载荷效果优于DIC法，但DIC法可获得腹板全场面外位移。

2) 给出了2种不同厚度下的无量纲载荷比-寿命曲线及载荷比-张力场系数曲线，并给出了满足舰载机寿命指标的机身加筋结构进入张力场程度控制的方法，可据此实现机身加筋壁板结构的轻量化设计。

3) 后续将对机身结构加筋壁板不同参数组合的反复屈曲疲劳特性及工程寿命评估开展进一步研究。