舰载机壁板剪切后屈曲承载能力预测与试验验证

刘存，张磊，杨卫平

航空工业第一飞机设计研究院 强度设计研究所，西安 710089

加筋壁板是舰载飞机的重要承载结构，在飞机着舰撞击构型下，蒙皮承受的剪应力会出现大于临界剪应力的情况，此时蒙皮开始失稳，由于壁板加强筋的存在，蒙皮失稳后还能够继续承受增加的外载荷，但其内力重新分配，失稳波纹数随之增多并趋于规则，最终可发生剪切后屈曲破坏。目前工程上对加筋壁板的剪切屈曲特性的计算仍在初始屈曲阶段，而需要考虑大扰度和塑性效应的工程后屈曲计算方法还不成熟。因此，采用有限元MSC.NASTRAN软件进行加筋壁板剪切后屈曲承载能力预测十分必要。

国内外学者对加筋壁板剪切后屈曲承载能力进行了研究。张国凡等[1]应用ABAQUS UMAT子程序，建立考虑渐进损伤的剪切破坏分析模型预估了复合材料加筋壁板在剪切载荷下的失效模式和失效载荷。Mallela和Upadhyay[2]采用有限元对承受面内剪切载荷下的复合材料加筋板进行了线性屈曲分析，但并没有进一步的后屈曲研究。Ambur等[3]采用ABAQUS建立了带初始几何缺陷的有限元模型，数值模拟了受面内剪切载荷下的复合材料加筋板后屈曲行为，并与试验进行了对比分析。田伟伟等[4]通过全场光学形貌扫描的方法得到了剪切载荷下铝合金加筋壁板屈曲模态的演变过程、光学离面位移数字结果，但仅限于试验测量，未通过有限元预测其破坏载荷。刘存和赵谋周[5]论述了加筋壁板面内剪切试验方法，通过试验得到了加筋壁板剪切后屈曲破坏载荷，仅用有限元分析了应力分布，未预测其后屈曲承载能力。王平安等[6]利用试验得到了剪切载荷下的复合材料加筋壁板屈曲特性，但仅通过有限元模拟与试验初始屈曲载荷进行了对比分析。冯宇等[7]用工程算法和有限元法对剪切载荷下的复合材料加筋壁板蒙皮初始屈曲载荷进行了计算，与试验结果吻合较好，但未涉及有限元预测其后屈曲承载能力。李爱环和支晗[8]通过PATRAN & NASTRAN分析剪切载荷下不同加筋尺寸对壁板蒙皮屈曲的影响，得到了屈曲载荷与腹板高度变化曲线，但没有分析其后屈曲承载能力。

在安全设计的前提下尽可能地减轻结构重量是飞机设计工程师一直努力的方向，而准确预测结构的承载能力直接关系飞机的安全性和减重设计。文中基于MSC.PATRAN软件对加筋壁板剪切试验件进行仿真建模，运用NASTRAN SOL105进行线性屈曲求解，采用一致缺陷模态法，运用FILED场将屈曲结果作为扰动引入后屈曲模型，考虑了加筋壁板后屈曲的大扰度和塑性效应，调用MARC非线性求解器对结构进行后屈曲计算，得到载荷施加点全过程的载荷-位移曲线、后屈曲模态、极限载荷及破坏模式，通过试验对比验证了该方法的准确性，在工程上为同类型加筋壁板剪切后屈曲承载能力的预测提供了方法和技术支持。

1 计算模型

1.1 加筋壁板剪切试验件

加筋壁板剪切试验件的考核区长度为700 mm，试验件的考核区由4个相同的长桁单元组成，长桁单元剖面如图1所示。考核区四周伸出过渡区用于与试验夹具相连，过渡区厚度为10.5 mm，宽度为150 mm，拉力为P1。试验件材料选用7150-T7751，其基本力学性能参数[9]如下：弹性模量Ec=73 700 MPa，屈服应力σ0.2t=524 MPa，极限强度σb=565 MPa，泊松比μ=0.33。

具体剖面参数如表1所示。其中：t为长桁腹板厚度；t1和b分别为长桁自由凸缘的厚度和宽度；t2和b1分别为长桁底边凸缘的厚度和宽度；h为长桁高度；R和R1为倒圆半径。

为了监测结构在剪切载荷下的后屈曲变形，在加筋壁板蒙皮和长桁的关键部位布置了应变片，试验件构型及应变测量点布置如图2所示，共142个测量点，长桁上布置单片，蒙皮表面布置花片，且正反面镜像分布。有限元模拟与试验对比分析所取的关键部位应变均来源于图2。

图1 试验件剖面图Fig.1 Cross-section of specimen

表1 试验件的剖面参数Table 1 Parameters of cross-section of specimen

参数蒙皮厚度/mm长桁参数/mmtt1t2bb1hRR1数值3.53.53.51.0282061.765

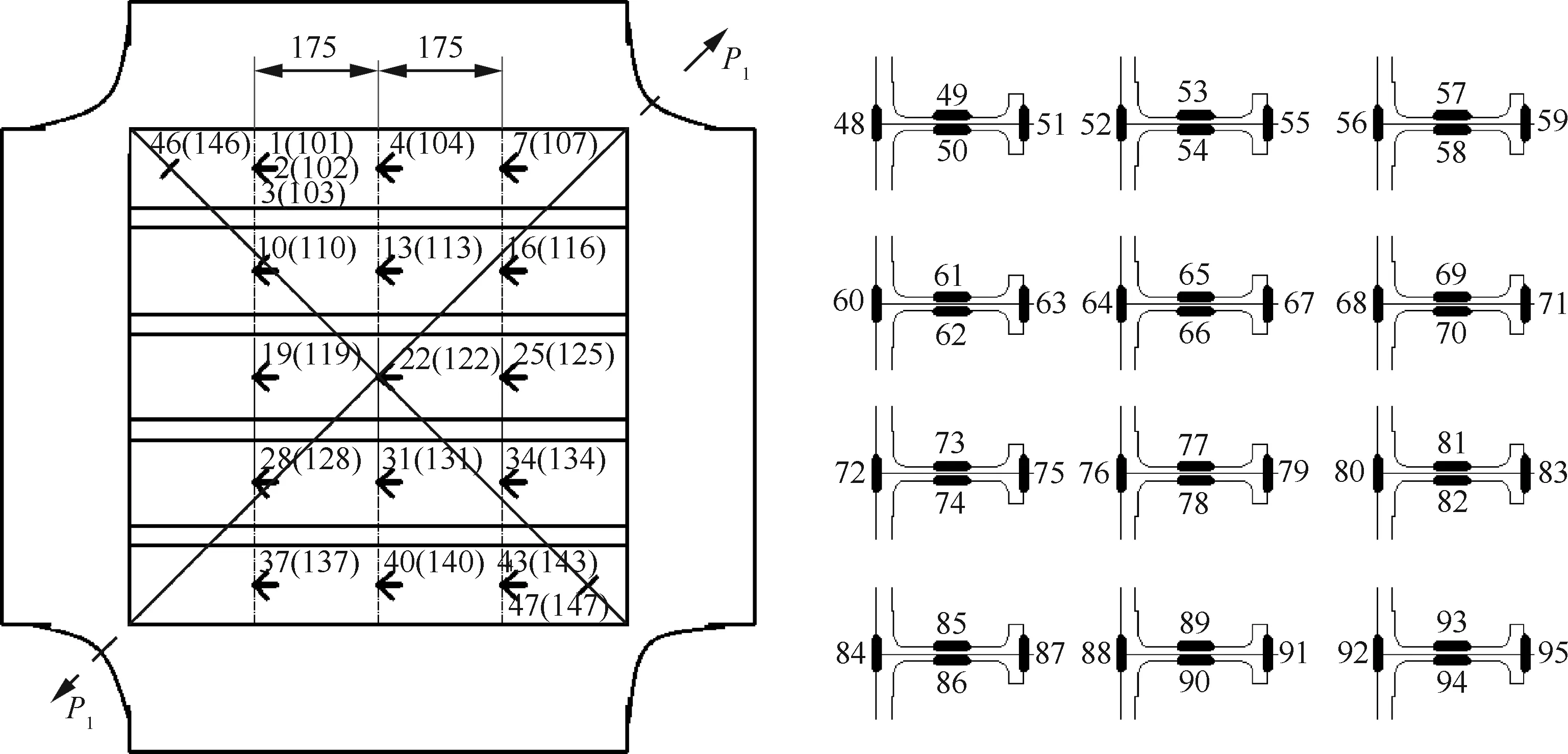
图2 试验件应变片布置图Fig.2 Layout diagram of strain gauge of specimen

1.2 有限元模型

有限元建模时，蒙皮和长桁的模拟采用四节点壳单元，考虑整体加筋壁板，长桁和蒙皮共节点。为了更好地模拟蒙皮的局部屈曲，采用细化的有限元模型。与压缩屈曲波相比，剪切屈曲波的波长较小，故在剪切载荷下需要足够细密的有限元网格来模拟剪切失稳波，每半波至少采用5个节点。加筋壁板剪切后屈曲破坏过程包含材料的弹性和塑性行为，为了准确地预测和模拟结构这一行为，采用材料真实的本构关系。铝合金7150-T7751板材[9]的应力-应变曲线如图3所示。

在MSC.PATRAN中定义材料弹塑性本构关系时，先输入弹性变形参数，定义材料的本构为弹性模型；再将该材料的本构模型指定为弹塑性，非线性应力应变数据通过FIELD调用图3中逐点输入的坐标。

采用类型为RBE2的多点约束单元模拟夹具与试验件连接。模型中处于对角拉伸方向上的加载点和约束点为主动节点，加载点约束垂向(Z向)位移，约束点约束蒙皮面内的X和Y向位移以及绕Z轴的转动位移。夹具与试验件用2排螺栓连接,其中心线对应的有限元节点为从动节点，分别约束其X或Y向自由度，同时约束其绕Z轴的转动位移。以便使模型达到试验状态下的约束。模型施加的载荷为强迫位移。有限元模型的加载和约束条件如图4所示。

图3 7150-T7751板材应力-应变曲线[9]Fig.3 Stress-strain curve of 7150-T7751 plate[9]

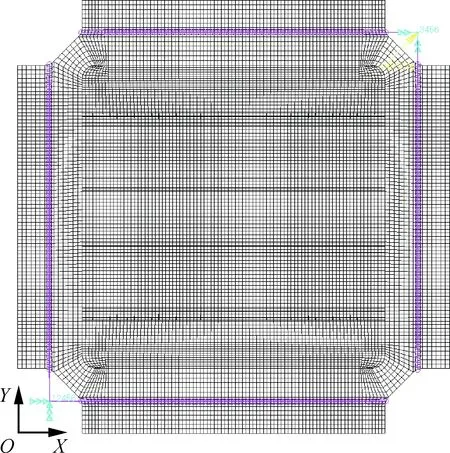
图4 有限元模型加载及约束图Fig.4 Loading and constrain conditions of finite element model

2 有限元模型的求解策略

建立能够真实反映结构抗屈曲性能的计算模型是进行加筋壁板剪切后屈曲计算的前提。然而求解要能够跟踪整个结构的平衡路径，能够跨越屈曲分叉点或极限强度点，又能够追踪整个失稳过程中实际的载荷-位移关系而获得结构失稳前后的全部信息，进而获得较为准确的结构后屈曲承载能力，需要制定求解策略。

首先要基于计算模型采用SOL105进行线性屈曲分析，获取结构的屈曲模态。其次将1阶屈曲模态乘以扰动系数，作为结构的初始缺陷，即一致模态缺陷。然后运用FILED将初始缺陷加入模型。在此基础上采用基于Newton-Raphson迭代的弧长法(Arc-Length Method)进行非线性有限元计算。

2.1 线性屈曲分析

线性屈曲分析通过提取使线性系统刚度矩阵奇异的特征值来获得结构的临界失稳载荷及失稳模态。MSC.NASTRAN软件SOL105为线性屈曲分析求解序列，适用于结构为小变形、单元应力必须是弹性(应力应变关系为线性)等范围内的求解，故对于非线性材料和大变形结构，SOL105计算得到的线性屈曲载荷和实际的临界载荷相差较大。根据最小势能原理，在仅考虑材料线弹性情况时节点外载荷矩阵F与节点位移矩阵u的关系为

KTu=F

(1)

式中：KT为切线刚度矩阵。

2.2 几何缺陷假定

由于制造工艺等因素，加筋壁板不可避免地存在一定的几何缺陷，如初始弯曲、初始偏心等。几何缺陷的实质是以附加应力的形式促使部分结构截面提前进入屈服，影响其承载能力。缺陷的存在使得结构的失稳一般都呈现为弹塑性状态，对其承载能力的分析应该是计及几何缺陷的弹塑性叠加几何非线性的双重非线性计算问题。

一致缺陷模态法[10]认为结构的最低阶临界点所对应的屈曲模态为结构的最低阶屈曲模态，结构按该模态变形将处于势能最小状态，所以对于实际结构来说，在载荷施加的最初阶段即有沿着该模态变形的趋势，如果结构的缺陷分布形式恰好与最低阶屈曲模态相吻合，这将对其受力性能产生最不利影响。一致缺陷模态法就是用最低阶屈曲模态来模拟结构的最不利几何缺陷的分布，并认为最低阶屈曲模态所对应的临界荷载就是该结构的最小临界荷载。采用这种缺陷形式主要面临2个问题：① 如何确定初始缺陷的模式；② 如何确定缺陷的最大值。Xu和Soares[11]利用有限元方法计算了5种不同构型的试验件在传感器测量的真实缺陷值(实测缺陷法)和认为假定缺陷(一致缺陷模态法)下的加筋壁板结构的承载能力，并与试验结果进行对比，结果表明引入实测缺陷计算得到的破坏载荷和破坏模式与试验结果吻合更好。万春华等[12]采用考虑几何和材料双重非线性的弧长法分析了初始几何缺陷对加筋结构后屈曲的影响，结果表明：当初始缺陷较小时，对结构的承载能力影响很小，但当初始缺陷增大至蒙皮厚度0.1倍以上时，载荷-位移曲线向下偏移。另外，相同模式、不同尺度的初始几何缺陷会得到不同的破坏模式。推荐在无实测结构初始几何缺陷情况下，以线性屈曲特征值法计算得到的1阶屈曲模态为初始缺陷模式，初始缺陷的最大位移值取蒙皮厚度的0.005～0.1倍。

文中通过SOL105线性屈曲特征值分析，得到加筋壁板剪切特征值屈曲模态。进行非线性屈曲分析前，将加筋壁板1阶屈曲模态矢量归一化，乘以缺陷基矢量10-3得到缺陷偏移矢量，通过SPCD模型数据卡来施加强迫节点位移，以更新单元节点坐标的形式将考核区的缺陷引入完善加筋壁板结构中。

2.3 非线性屈曲分析

在增量加载过程中，用包含加载过程中所有非线性影响的刚度矩阵来评定屈曲特征值，求得的失稳载荷更接近结构的真实临界载荷值。通过增量定义的非线性屈曲分析，可以同时考虑材料和几何非线性对结构稳定性的影响，选中材料本构关系后，在增量加载分析中激活LGDISP等选项，程序会自动地在几何非线性的基础上计算材料非线性对刚度矩阵的贡献[13]。

在考虑材料和几何双重非线性的后屈曲分析中[14]，式(1)中的切线刚度矩阵KT应改为

KT=Kep+Kgs+Kld-KR

(2)

式中：Kep为结构弹塑性矩阵；Kgs为几何刚度矩阵；Kld为大位移刚度矩阵；KR为载荷矫正矩阵。

在每一子步的切线刚度求解完成后，采用基于Newton-Raphson迭代的弧长法进行子步位移增量计算，Newton-Raphson迭代公式为

φ(un)=KTun-F

(3)

(4)

un+1=un+Δunn=1,2,…

(5)

式中：φ(un)为第n步的剩余载荷；KTn为第n步的切线刚度矩阵；un和un+1为第n和n+1步的位移向量；Δun为位移增量。

由于Newton-Raphson方法无法计及刚度系数等于零的情况(通常对应于极限载荷点)，而对于非线性后屈曲求解来说，主要目的在于探究结构的极限载荷点和追踪平衡路径，而弧长法在增量步中加入弧长约束来实现刚度系数过零的力学状态。具体弧长迭代公式为

(6)

式中：A0为常量；Δλi为载荷因子；ΔI为控制弧长。

弧长法分析屈曲问题不仅考虑刚度奇异失稳点附近的平衡，而且是通过追踪整个失稳过程中实际的载荷-位移关系，获得结构失稳前后的全部信息。弧长参数选择得当，可完整跟踪包括屈曲非稳定段的载荷-位移曲线。后屈曲模型采用NLPARM卡定义非线性分析，载荷被分为52个等增量，采用ITER方法控制切线刚度修正，矩阵修正之前的迭代次数为40，每个载荷增量的总迭代限为1 000。采用NLPCI卡定义非线性静态分析中弧长增量求解策略，弧长法类型为MRIKS，最小弧长比为0.25，最大弧长比为4.0，期望收敛的迭代次数为40，每步最大迭代次数为500。采用弧长法进行每个载荷步的位移及切线刚度求解，每个子步重复迭代直到满足收敛条件，最后根据每个载荷步内的计算结果绘制载荷-位移曲线，依据曲线得到加筋壁板结构的双重非线性后屈曲极限载荷。

3 后屈曲承载能力预测与试验验证

3.1 屈曲和破坏载荷

对几何参数如表1所示的3件加筋壁板剪切试验件进行了试验，屈曲载荷试验结果与有限元结果的比较如表2所示，破坏载荷试验结果与有限元结果的比较如表3所示，同时给出了试验载荷平均值。表中ε为有限元计算值相对于试验值的误差，即

ε=(PFEA-PTEST)/PTEST×100%

(7)

式中：PTEST为试验值；PFEA为有限元计算值。

可见，采用有限元计算的加筋壁板剪切后屈曲的初始屈曲载荷和破坏载荷与试验值误差均在5%以内，有限元仿真计算得到的初始屈曲载荷与试验载荷平均值误差为1.25%，破坏载荷平均值误差为2.4%。

表2屈曲载荷试验结果与有限元结果比较

Table2Comparisonofbucklingloadsbetweentestresultsandcalculationresults

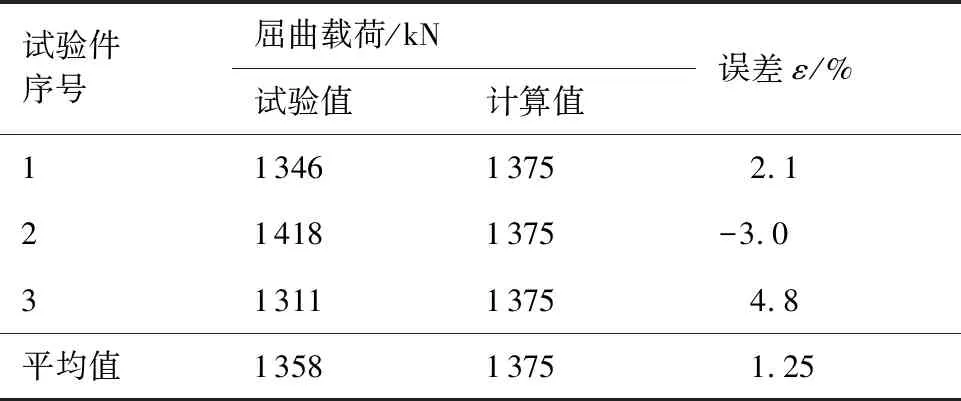
试验件序号屈曲载荷/kN试验值计算值误差ε/%113461375 2.1214181375-3.0313111375 4.8平均值13581375 1.25

表3破坏载荷的试验与有限元结果比较

Table3Comparisonoffailureloadsbetweentestresultsandcalculationresults

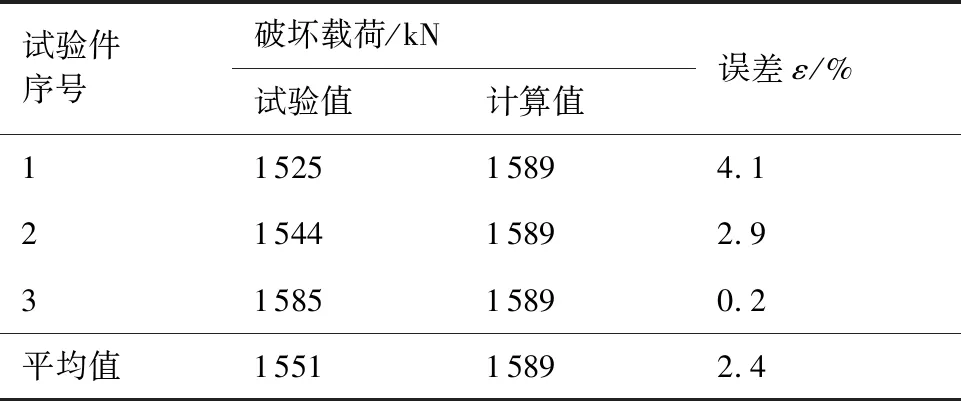
试验件序号破坏载荷/kN试验值计算值误差ε/%1152515894.12154415892.93158515890.2平均值155115892.4

3.2 载荷-位移曲线

利用SOL105模块进行加筋壁板剪切试验件有限元模型的线性屈曲分析，计算得到的屈曲模态如图5所示，1阶失稳特征值的临界失稳系数为0.98，计算得到屈曲载荷为1 375 kN，即在98%的设计载荷时加筋壁板发生初始屈曲。此外，加筋壁板的蒙皮发生局部屈曲，关于对角拉伸线呈现反对称分布的剪切屈曲波，单侧出现由4个屈曲半波构成的2个完整屈曲波形，4根长桁均未发生局部屈曲，处于波形的节点上，起到了隔波的作用。

提取加筋壁板剪切试验件考核区结构各点弹性屈曲位移，按照一致缺陷模态法将所得到位移按比例因子10-3进行折算，利用MSC.PATRAN中位移的FIELD定义模式施加，引入扰动的加筋壁板等值线图与初始屈曲模态形貌完全一致。在求解设置中开启大变形(LGDISP)考虑几何非线性，引入材料的弹塑性曲线，在弧长法中设置合适的载荷步和弧长增量，进行非线性迭代计算。提取载荷及位移的计算结果，绘制载荷-位移曲线如图6所示。

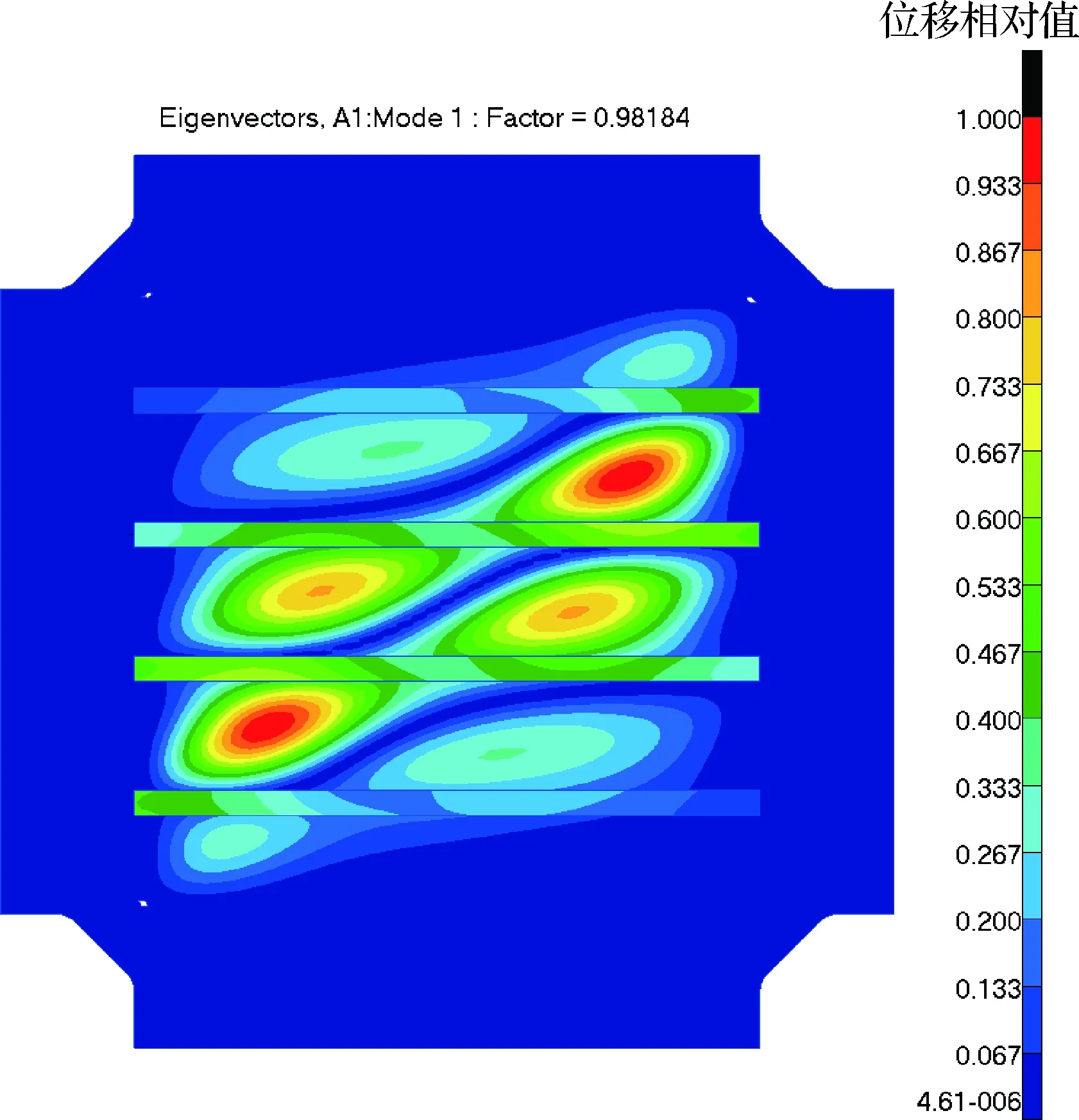
图5 加筋壁板的初始屈曲模态Fig.5 Initial buckling modes of stiffened panel

由加筋壁板加载端载荷-位移曲线可见，曲线在初始阶段呈线性，加载到1 364 kN时，曲线斜率略微下降，此时结构出现初始屈曲，结构面内剪切刚度发生变化，进入后屈曲阶段，采用非线性分析中基于曲线获得的屈曲载荷与特征值线性屈曲分析结果1 375 kN基本一致，表明有限元分析模型对于出现屈曲前的线性加载阶段的模拟准确。而实际试验中剪切试验件的初始屈曲载荷平均值为1 358 kN，相对误差为1.25%。随着载荷继续增加，在出现拐点前曲线斜率小幅下降，最终曲线在1 589 kN时达到顶点，即结构的极限载荷。随后，曲线斜率为负值，位移继续增加，载荷下降，结构丧失承载能力。实际试验中剪切试验件的破坏载荷平均值为1 551 KN，相对误差为2.4%。

非线性有限元仿真计算加筋壁板试验件的初始屈曲载荷为破坏载荷的86.5%，而实际试验的初始屈曲载荷平均值为破坏载荷平均值的87.5%。可见3.5 mm厚的加筋壁板剪切试验件在发生剪切屈曲后仍能继续承载，直到发生结构破坏。

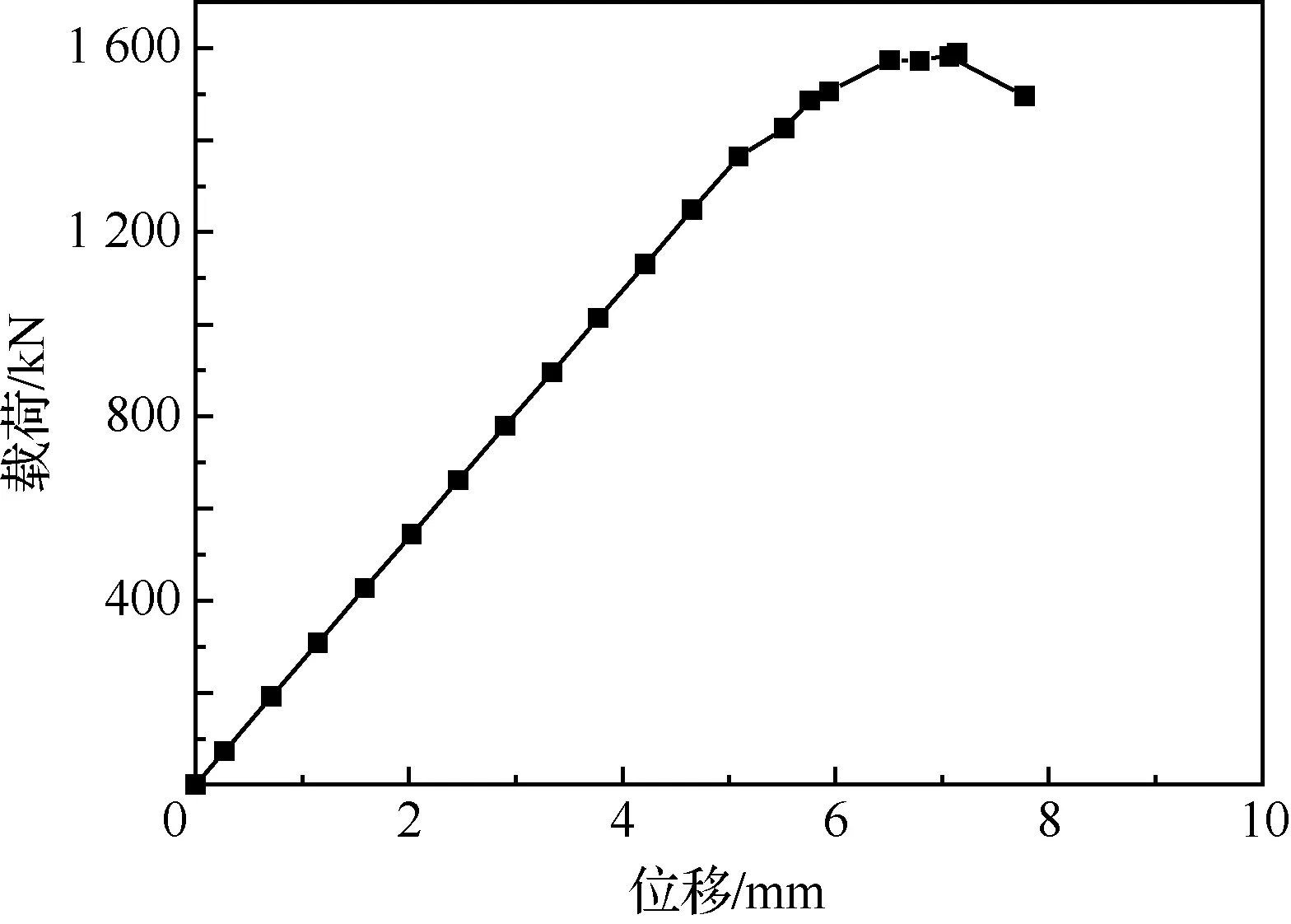
图6 加筋壁板加载端载荷-位移曲线Fig.6 Load-displacement curve of loading end

3.3 破坏模式

为进一步分析破坏过程，对加筋壁板剪切试验件考核区蒙皮在加载过程中的位移变化过程进行分析。破坏模式是蒙皮先发生局部屈曲，随着载荷增加，局部波形扩大并穿越长桁导致加筋板破坏。有限元模拟破坏时刻位移云图如图7所示，试验第1#件的破坏形貌如图8所示。文中仅对第1#件的试验数据与有限元模拟结果进行对比分析，可见两者的破坏部位和破坏模式一致。

结合试验录像过程及试验件的最终破坏形貌对剪切屈曲波描述如下：在试验件对角拉伸的两个角区，一个向蒙皮侧凸起，另一个则向长桁侧凹陷，同时角区产生小的屈曲波；在对角拉伸线的两侧交替分布着凸起和凹陷的屈曲波，波长和波深随载荷的增大而变化；随着载荷的继续增加，屈曲波产生的面外变形持续增加，在大挠度和塑性效应的作用下，长桁和蒙皮开裂，进而蒙皮破坏。从试验件的破坏形貌和有限元仿真破坏变形图可见，两者最终破坏模式基本一致。

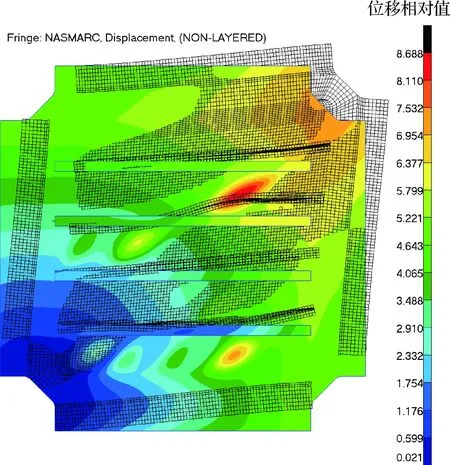
图7 有限元模拟破坏时刻变形云图Fig.7 Deformation morphology of FE simulation failure

图8 剪切试验件的试验破坏形貌Fig.8 Failure morphology of shear specimen in test

3.4 破坏过程

剪切试验件处于纯剪切状态，22#和122#应变片位于壁板考核区中心点上，且在加载对角线上,25#和125#应变片位于考核区中心点附近。考核区中心点长桁侧22#和蒙皮侧122#应变片以及25#和125#应变片的应变随加载步变化曲线的计算值与试验值的对比如图9所示，图中，“试验”为实测应变花合成最大剪应变(试验-22代表22#、23#、24#应变片合成的最大剪应变，其他类同)，“有限元”为有限元仿真最大剪应变。剪切试验件角区长桁侧43#和蒙皮侧143#应变片的应变随加载步变化曲线的计算值与试验值的对比如图10所示。

从图9可见，试验件中心点蒙皮处(应变花22#、122#)的载荷-应变曲线均在起始阶段呈现线性变化，在载荷增加到1 346 kN左右时，试验与有限元分析得到的载荷-应变曲线均出现了明显的拐折，据此推断该处产生了较大的面外位移，即发生了局部屈曲。其中，屈曲点的判断为背对背的应变平均值随载荷变化曲线斜率发生明显变化的拐折点。图10所示的加筋壁板角区有限元与试验载荷-应变曲线的屈曲载荷为1 485 kN，与中心点相比，明显较晚，这与角区边界支持刚度较强有关。图9和图10显示有限元分析和试验实测曲线在线性段吻合很好，结构发生屈曲后，进入材料非线性和几何非线性交织状态，有限元分析和试验实测曲线变化趋势基本一致，但存在一些偏差，这对采用有限元准确模拟加筋壁板剪切试验件的后屈曲过程提出了更高要求。有限元仿真得到的破坏模式与试验一致，关键部位的载荷变化曲线与试验数据吻合较好，承载能力计算值与试验值基本一致，达到了采用NASTRAN预测加筋壁板剪切后屈曲承载能力的目的。

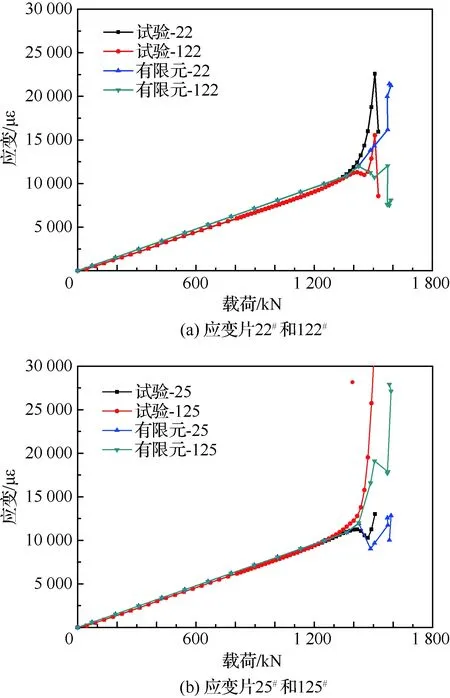
图9 加筋壁板中心有限元分析与试验所得载荷-应变曲线对比Fig.9 Comparison of load-strain curves obtained by FEA and test at stiffened panel center point

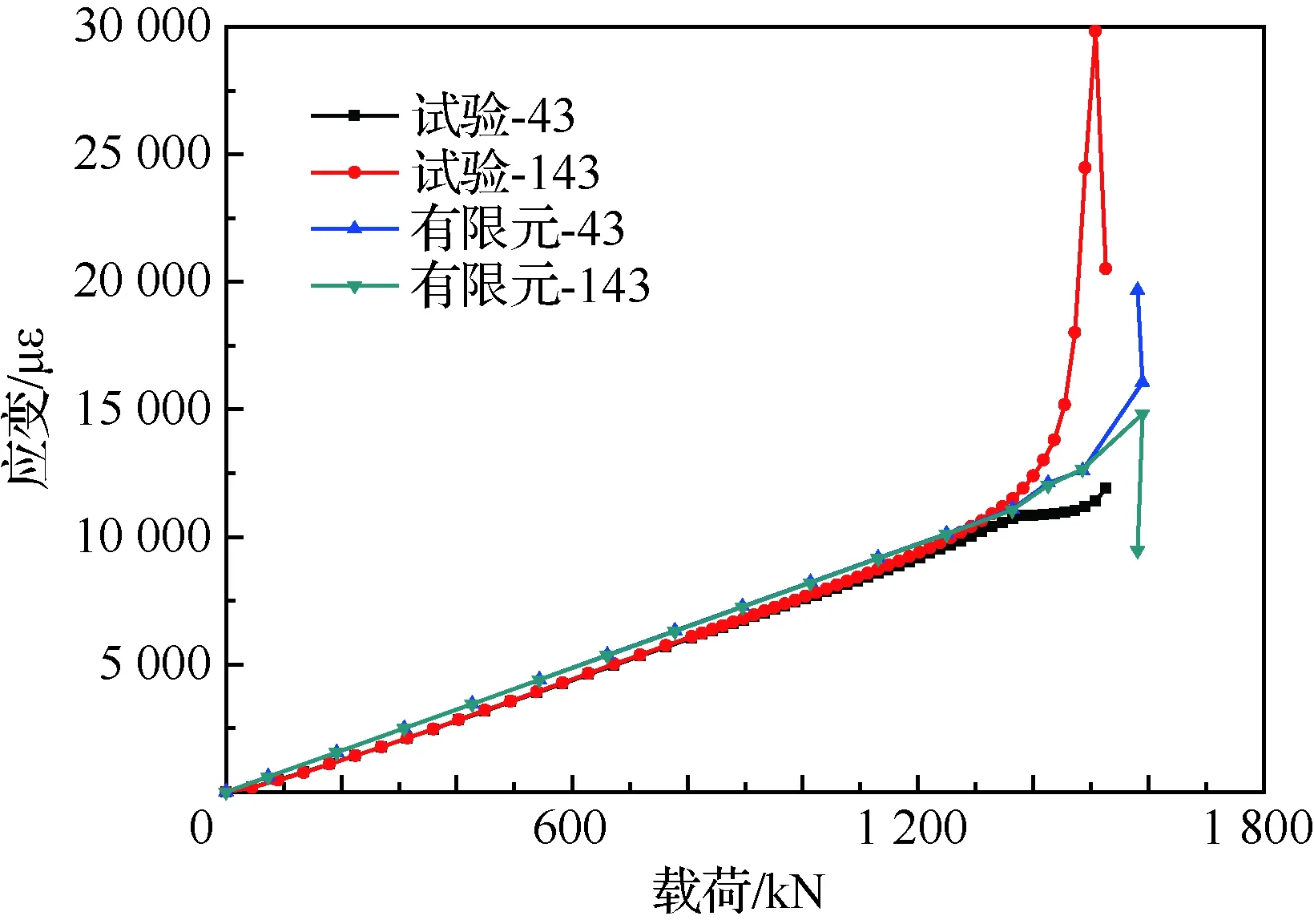
图10 加筋壁板角区有限元分析与试验所得载荷-应变曲线对比Fig.10 Comparison of load-strain curves obtained by FEA and test at stiffened panel corner point

4 结 论

通过对加筋壁板受面内剪切载荷全过程的分析及试验验证，得到以下结论：

1) 采用MSC.NASTRAN模拟了加筋壁板受面内剪切的全过程，包括其载荷-位移曲线的初始线性、结构后屈曲承载能力和结构的破坏模式。

2) 基于文中有限元模拟的屈曲载荷、破坏载荷、破坏模式和典型位置的应变与试验对比结果，印证了有限元预测模型的有效性。

3) 引入初始缺陷，考虑了双重非线性的NASTRAN有限元预测模型，工程上可作为加筋壁板强度预估的一种有效手段。