柔性航天器振动主动抑制及姿态控制

张秀云，宗群，窦立谦,*，刘文静

1. 天津大学 电气自动化与信息工程学院，天津 300072 2. 北京控制工程研究所 空间智能控制国家重点实验室，北京 100190

航天器是指按照天体运行规律在大气层外运行的空间飞行器，在天气预测、经济发展、环境监测、国家安全等方面发挥着日益重要的作用。为满足日益增加的航天需求，航天器需携带柔性太阳帆板，而在航天器完成机动、转向及空中对接等动作时，很容易激起柔性帆板的振动，从而严重影响系统的稳定性。此外，航天器在运行过程中受到太阳光压力矩、重力梯度力矩、地球非球形摄动等外部干扰，这也为控制器设计带来极大的挑战。因此，干扰影响下柔性航天器的高精度快速姿态控制是目前研究的热点及难点问题。

近年来，针对干扰影响下的航天器姿态控制问题，国内外研究者们提出了各类控制方法：H∞控制[1]、输出反馈控制[2]、滑模控制[3-4]等，其中，滑模控制方法得益于其对干扰的强鲁棒特性，得到了广泛的应用[5-7]。文献[8]针对干扰影响下的刚体航天器姿态控制问题，设计终端滑模控制器，实现了航天器精确姿态跟踪，但其控制器存在奇异性。针对该问题，国内外学者进行了相应改进[9-10]，提出非奇异终端滑模。北京理工大学夏元清等[11]进一步提出自适应非奇异终端滑模，实现刚体航天器姿态的有限时间稳定，但其仅能收敛到原点附近小邻域内。天津大学宗群等[12-14]则针对刚体航天器姿态控制问题，利用自适应干扰观测器-终端滑模控制器综合设计方法，保证姿态的有限时间稳定。以上文献大多针对刚体航天器姿态控制问题，未考虑柔性附件振动影响，且大多仅能保证刚体姿态有限时间收敛到小邻域，并不能实现姿态的精确收敛。

针对航天器柔性附件振动抑制问题，现有文献主要分为2种解决思路：被动抑制及主动抑制。被动抑制即将柔性振动视为系统不确定影响，利用控制器的鲁棒性进行处理[15]，但其振动仍旧存在。而柔性振动主动抑制则通过外加指令，直接对振动进行抑制，如输入成形器(Input Shaper，IS)等。作为一种有效抑制柔性振动的前馈控制方法，输入成形器得到了广泛的研究。其作用原理为：通过利用振动频率及阻尼信息，设计其作用脉冲及幅值，保证加入系统后产生的振动响应能够相互抵消[16-18]。输入成形器技术可用于解决柔性航天器的振动抑制问题。哈尔滨工业大学胡庆雷团队[19]通过结合输入成形器及滑模控制方法，解决了干扰影响下的柔性航天器控制，但其需要干扰上界已知。文献[20]则提出一种输入成形器与自适应滑模结合的方法，无需干扰上界已知，且保证柔性航天器姿态控制，但其仅能保证姿态的渐近收敛，难以满足航天器姿态控制的快速性要求。

在上述研究基础上，本文针对干扰及不确定影响下的柔性航天器姿态控制问题，提出了输入成形器-自适应有限时间干扰观测器-有限时间积分滑模控制器综合的设计方法，避免了干扰上界必须已知的限制，保证了干扰估计误差有限时间收敛至零，实现了柔性航天器姿态的有限时间精确控制及有效的柔性附件振动抑制。

1 柔性航天器数学模型

采用单位四元数描述航天器姿态，则航天器运动学模型描述为[14]

(1)

考虑航天器柔性附件发生变形振动，系统姿态动力学方程及柔性振动方程可描述为[21]

(2)

(3)

(4)

基于式(1)～式(3)，得到姿态跟踪误差动力学为[14]

(5)

(6)

(7)

式中：Y=T-1。

基于动力学模型式(5)及式(6)，对式(7)求导可得

(8)

式中：J*=YTJY∈R3×3；综合干扰D∈R3包含系统外部干扰(如重力梯度、太阳光压等干扰力矩)及柔性振动主动抑制后的残余振动带来的内部干扰，记残余振动模态为χc。

(9)

性质2[22-23]惯性矩阵J*满足：

(10)

式中：λmax、λmin为正常数。

本文的控制目标表述为：针对柔性航天器姿态系统式(1)及式(2)，研究柔性振动主动抑制方法，设计控制器u(t)，实现对期望姿态的有限时间精确控制，即

(11)

式中：T为收敛时间。

2 航天器有限时间控制器设计

本节将针对航天器模型式(8)进行控制器设计，所采用的控制策略如图1所示，主要包括输入成形器、自适应有限时间干扰观测器及有限时间积分滑模控制器3部分。首先，基于振动模态的自然频率及阻尼信息设计输入成形器，并与姿态参考输入进行卷积，获得期望参考输入；其次，基于系统姿态及控制输入信息，设计自适应有限时间干扰观测器，实现对干扰及残余柔性振动影响的精确估计；最后，基于观测器估计值，设计有限时间积分滑模控制器，实现对期望参考输入的高精度快速跟踪。

图1 综合控制策略设计框图Fig.1 Block of integrated control strategy

2.1 自适应有限时间干扰观测器设计

基于航天器系统式(8)，设计如下干扰观测器：

(12)

式中：

(13)

(14)

其中：ρ=κL2+η，κ为待设计正常数，η为任意小的正常数；δ(t)的表达式为

(15)

式中：veq为等价输出注入项[24-25]；0<α<1；ε为任意小的正常数。

基于式(8)及式(12)，对状态估计误差e求导可得

(16)

(17)

(18)

(19)

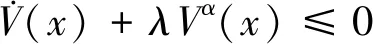
式中：V(x0)为V(x)的初值，x0为初始状态。

注2有限时间收敛是指系统状态在有限时间内到达平衡点并一直保持在该平衡点上。该概念广泛应用于航空航天控制系统、机器人控制系统、电机控制系统等诸多实际领域，具有重要的实际应用意义[26-27]。此外，由引理1及引理2有限时间Tr的表达式可以看出，只要已知系统初始状态x0，则有限收敛时间Tr的值就可以事先确定。

定理1针对航天器姿态控制系统式(8)，设计自适应有限时间干扰观测器式(12)、式(13)，参数自适应律如式(14)所示，则观测器的状态估计误差e及干扰估计误差会在有限时间内收敛到0。

第1步定义Lyapunov函数为

(20)

-η|δ(t)|

(21)

根据式(21)及引理1可知，δ(t)会在有限时间T1内收敛到0。

当δ(t)=0后，由于0<α<1，ε>0，并基于式(17)，可以得到

(22)

第2步定义Lyapunov函数为

(23)

基于性质1，对V2求导可得

(24)

(25)

(26)

注3根据观测器式(12)～式(14)，可以看出无需综合干扰上界信息已知，消除了上界约束；另外，通过对定理1的证明可知，本文所设计的自适应有限时间干扰观测器可以保证干扰估计误差有限时间收敛到0。

2.2 有限时间积分滑模控制器设计

针对航天器姿态系统式(8)，设计如下积分滑模面：

(27)

(28)

由积分滑模面式(27)可以看出，当t=0时，s=0，即系统状态在初始时刻时就在滑模面上，消除了滑模面的到达过程，保证了全局的鲁棒性。

基于积分滑模面式(27)，可得滑模动态为

(29)

控制器设计为

(30)

引理3[28]考虑如下积分链系统：

(31)

式中：xi(i=1,2,…,n)为系统状态变量；τ为系统控制输入。

若控制器设计为

(32)

定理2针对航天器姿态控制系统式(8)，基于积分滑模面式(27)及自适应有限时间干扰观测器式(12)～式(14)，设计如式(30)所示的有限时间积分滑模控制器形式，则航天器姿态跟踪误差qev及角速度跟踪误差ωev会在有限时间收敛到0。

证明首先证明在自适应有限时间干扰观测器误差收敛到0之前，系统状态不会发散；其次证明干扰观测器观测误差收敛到0之后，系统状态跟踪误差将在有限时间内收敛到0。

第1步定义Lyapunov函数为

(33)

对V3进行求导，并代入式(29)、式(30)可得

(34)

第2步当干扰观测器的观测误差收敛到0之后，系统滑模动态变为

(35)

此时，可以得到

(36)

(37)

3 输入成形器

输入成形器是指具有一定作用幅值及作用时间的脉冲序列，利用合适的输入成形器与系统参考指令相卷积，改变系统输入的形状和作用位置点，达到抑制柔性振动的目的。

最基本的输入成形器为2个作用脉冲，为获得输入成形器形式，基于系统振动的频率及阻尼信息，建立振动响应表达式，并考虑以下约束条件：加入脉冲后的振动响应为0，且尽量减小成形器的作用时间，并保证不影响系统姿态的最终期望值等。建立如下约束方程组[16]：

(38)

式中：Aj为第j个脉冲的振动幅值，此时考虑的为2个脉冲；tj为第j个脉冲的作用时间；Ω0为振动频率；ξ为阻尼。

通过求解方程式(38)，得到两脉冲零振动输入成形器(Zero-Vibration，ZV)形式为

(39)

输入成形器具有多种形式[16]：ZV、ZVD (Zero Vibration and Derivative)、EI (Extra-Insensitive)等，其各具特点。其中ZV作用时间最短，但由于干扰等影响导致系统实际振动频率不等于固有频率时，其抑制效果不理想，即不具有鲁棒性；ZVD作用时间与EI作用时间相同，且EI的鲁棒性相对较强，但当航天器的真实频率等于固有频率时，EI仍存在残余振动。因此，综合考虑各类输入成形器的优缺点，选择ZVD对航天器柔性振动进行抑制，通过在方程式(38) 中增加对振动响应导数的约束，可得ZVD表达形式如下：

(40)

(41)

式中：“*”为卷积作用。

4 仿真分析

为验证本文所提输入成形器-自适应有限时间干扰观测器-有限时间积分滑模控制器综合方法的有效性，进行仿真验证与分析。仿真中，各参数选取如下：

考虑前三阶柔性振动模态，则卫星主体与柔性附件的耦合矩阵δ为

δ=

柔性模态自然频率参数为：Λ1=0.768 1 rad/s,Λ2=1.103 8 rad/s,Λ3=1.873 3 rad/s。

柔性模态阻尼比为：ξ1=0.005 6，ξ2=0.008 6，ξ3=0.013。

所受到的干扰设置为

d=

[0.1sin(2t) 0.05cost+0.2sint0.08cos(3t)]T

航天器姿态及角速度初值为

期望姿态与角速度为

输入成形器设计为

干扰观测器及控制器参数选取如表1所示。

仿真结果如图2～图6所示。图2为航天器姿态及姿态角速度跟踪曲线。可以看出，姿态及姿态角速度均能在有限时间内收敛至平衡点，收敛时间约为20 s，精度数量级达到10-4，因此，加入输入成形器未影响系统的跟踪精度及收敛时间。图3为系统综合干扰的估计及估计误差曲线。可以看出，本文设计的自适应有限时间干扰观测器可以保证对综合干扰的精确估计。图4为系统控制输入曲线。可以看出，控制输入范围合理。图5为滑模面变化曲线。系统状态在15 s左右重回滑模面，即滑模面在有限时间收敛到0，验证了控制算法的有效性。由于对系统产生主要作用的即为一阶振动模态，其他模态影响较小，因此，通过针对一阶振动模态加入输入成形器，得到如图6所示的一阶柔性振动模态变化。可以看出，与未加输入成形器时相比，加入后可有效抑制75%的柔性附件振动，具有良好的柔性振动抑制效果。

表1 观测器及控制器参数设置Table 1 Parameter settings of observer and controller

图2 姿态角和姿态角速度跟踪误差Fig.2 Attitude angular and velocity tracking errors

图3 综合干扰估计和估计误差Fig.3 Estimation and estimation error of lumped uncertainty

图4 控制输入Fig.4 Control inputs

图5 滑模面变化曲线Fig.5 Sliding mode surface

图6 柔性振动模态Fig.6 Flexible vibration mode

因此，通过仿真可以验证，本文所设计的输入成形器-自适应有限时间干扰观测器-有限时间积分滑模控制器综合方法能够有效抑制柔性附件振动，且能保证系统姿态的高精度快速收敛。

5 结 论

1) 本文提出了一种新型自适应有限时间干扰观测器设计方法，无需综合干扰上界信息，且能够保证干扰估计误差有限时间收敛至零。

2) 基于干扰观测器对系统综合干扰的估计值，设计了有限时间积分滑模控制器，保证系统姿态跟踪误差及角速度跟踪误差有限时间收敛到零。

3) 利用输入成形器对系统参考指令进行变形，获得期望参考输入，解决航天器柔性振动主动抑制问题，并将抑制后的残余振动利用观测器进行估计并在控制器设计中进行补偿，保证姿态控制的高精度，实现输入成形器-自适应有限时间干扰观测器-有限时间积分滑模控制器综合的有限时间快速精确控制。