基于动态重叠网格方法的尾翼对螺旋桨滑流的影响

缪涛，陈波, *，马率，杨小川，丁兴志

1. 中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000 2. 航空工业第一飞机设计研究院，西安 710089

涡轮螺旋桨发动机具有耗油率低、巡航状态经济效率高和低速飞行时推力大等特点，在当前中速远程运输机、旅客机、海上巡逻机、反潜机等领域仍然广泛采用螺旋桨推进。如欧洲空客A400运输机，美国C130“大力神”运输机、P-3C反潜巡逻机，中国研制的新舟60/700、运7、运8和运12飞机等。

螺旋桨飞机在研制过程中气动设计阶段必须要着重考虑螺旋桨滑流对全机的气动性能干扰，这种滑流干扰比涡轮喷气发动机的影响更加突出，甚至可以决定整个飞机设计的成败。由于滑流显著的三维非定常效应，在设计阶段如果引入非定常带动力滑流影响，需要考虑各种拉力系数的极端条件和起降构型中襟副翼偏转等实际情形，若再考虑部件优化选型等工作，整个计算量将十分巨大。因此，在研制初期开展螺旋桨滑流对飞机气动性能干扰影响的研究不仅关乎飞机起降安全、意义重大，同时也极具挑战。

当前通过数值计算手段来研究螺旋桨滑流主要采用以下3种方法：① 全桨叶旋转的非定常数值模拟方法。夏贞锋[1]发展了基于动态面搭接网格技术的非定常数值模拟方法和基于激励盘理论的准定常模拟方法，主要研究了滑流对飞机气动特性的影响、机翼对滑流流动的干扰以及机翼对螺旋桨气动特性的影响3个方面。杨小川[2]发展了针对旋转机械的动态拼接网格计算方法，针对某涡桨飞机对比了定常和非定常两种计算方法下的计算结果，研究了桨叶非定常的滑流效应。Lenfers等[3]开展了考虑螺旋桨滑流时高升力机翼构型的计算与试验研究，分析了不同拉力系数下滑流对机翼表面压力分布和极限流线的影响规律。Roosenboom等[4]开展了螺旋桨滑流的粒子图像测速(PIV)试验测量工作，对比了不同拉力系数下空间切面的平均速度、脉动量及湍动能，并将其与非定常数值计算结果进行对比[5]，不仅直观刻画了三维滑流的流动特征，也显示出当前主流CFD方法在预测滑流中具有相当高的精度和巨大潜力。② 采用激励盘理论的准定常模拟方法。陆浩[6]改进了等效盘模型并通过试验结果进行了验证，开展了螺旋桨滑流与短舱/进气道干扰流场的数值模拟研究。李博等[7]发展了等效盘模型方法，并针对某四发涡桨飞机开展了有/无滑流下全机流场研究。③ 多重参考系方法。任晓峰等[8]采用多重参考系方法开展了螺旋桨滑流对尾翼区流场特性研究，通过变化平尾位置增加了飞机的纵向静稳定性。王科雷等[9]采用多重参考系方法对3种螺旋桨-机翼构型的低雷诺数气动特性进行了数值模拟，通过对比机翼气动力系数及表面流场结构特征分析了分布式螺旋桨滑流对机翼的气动影响。

上述第1种方法真实模拟螺旋桨的旋转运动，但对计算网格与资源要求较高，后两种方法对螺旋桨旋转现象进行适当的简化，将非定常问题简化为定常计算，大大降低了计算和求解难度。

国内外研究滑流的具体问题及对象已经比较全面，包含滑流与机翼[10-13]、短舱[14]、进气道[15-16]、平尾[17-19]相互干扰等方面。滑流对尾翼的干扰会严重影响飞行品质，在飞机设计时如果由于客观约束，在典型设计点要求尾翼必须沉浸于滑流的主流区域时，如何准确分析滑流与尾翼的相互干扰，则成为了一个必须克服的问题。由于滑流是位于尾翼的前方来流，滑流势必会对尾翼的绕流场和表面气动力产生影响，但是研究尾翼是否对滑流区域也同样产生影响，产生多大影响，在多大空间范围内产生影响，相比于飞机自身的气动力，这个影响量是否可以忽略等问题有助于将滑流与尾翼的干扰解耦，如果尾翼对滑流的影响不可忽略，则在设计尾翼外形和空间布局时必须要同时考虑滑流和尾翼；而如果尾翼对滑流的影响在一定程度内可以忽略，则在设计时可简化为三维无尾构型的滑流非定常计算和尾翼在滑流收敛流场的局部绕流计算两个步骤。相比通常的准定常滑流模拟方法，这样既更加精确模拟了滑流的非定常效应，又大大节约了尾翼布局选型时的计算资源，缩短研制周期。

为了解答上述问题，本文采用三维动态重叠网格的方法，首先对某螺旋桨飞机带尾翼构型进行了数值模拟，通过试验结果对计算方法进行验证。在此基础上，分别开展了有/无尾翼构型的滑流计算，通过分析全机气动力、空间切面速度分布云图、不同空间位置和拉力系数的下洗角和侧洗角变化曲线，探讨了尾翼对滑流的影响规律。

1 数值计算方法

流场计算采用自主开发CFD软件PMB3D[20]，流动控制方程为雷诺平均可压缩Navier-Stokes方程，在惯性坐标系下的积分形式为

(1)

相比于无动力定常计算，在模拟带动力螺旋桨旋转产生的非定常滑流时，需要在以下3个方面做特殊处理：① 控制方程。如果将控制方程建立在随螺旋桨旋转的非惯性系，并在此坐标系下求解流场，则需要在控制方程中增加反映坐标系旋转的源项。本文控制方程均建立在固连飞机的惯性坐标系上，在模拟螺旋桨旋转运动时，直接模拟网格单元的相对运动，在运动单元的通量计算中，将控制体的网格运动速度与控制体内部的流体运动速度一并考虑，从而实现对运动网格单元的模拟。② 空间离散网格。解决桨叶网格的运动问题时，较为成熟的方法是结构网格框架下的动态重叠(Chimera)网格方法[21]。重叠网格对相对运动的部件生成不同的网格，分别随各自部件运动，相互之间构成动态的重叠关系，在飞机网格与桨叶网格交接区域，需要调整好网格密度以及均匀程度，以满足重叠插值的要求。③ 动态重叠网格插值效率。为节约动态重叠网格每一时间步的插值计算开销，考虑螺旋桨桨叶是定轴匀速转动，在计算中只在第一周期内建立各网格间的插值关系并用文件形式储存，从第二周期开始，直接读取文件获得插值关系，不需重新进行重叠网格的挖洞、贡献单元的搜寻与确定插值系数等一系列操作，这一策略在实际应用中大约能节省20%～30%的计算开销。

2 滑流计算结果验证

2.1 计算模型及空间网格

为验证计算程序和方法的正确性，对某机身+机翼+短舱+螺旋桨+尾翼构型飞机的滑流结果进行验证，同时考虑内侧襟翼和外侧副翼的偏转，外形如图1所示。在计算时采用重叠结构网格方法，在螺旋桨与襟翼、副翼处采用重叠子网格，飞机其他部件为对接网格，桨叶网格随桨叶一起作刚体运动，动态地与全机背景网格构成重叠关系。第1层网格物面距离为1×10-5m，满足y+≈O(1)，全机网格量约为5 000万，包含642个网格块，空间网格示意图如图2和图3所示。

图1 有尾构型外形示意图Fig.1 Sketch of with-tail-wing configuration

图2 物面网格与空间拓扑前视图Fig.2 Front view of surface grid and space topology

图3 物面网格与空间拓扑仰视图Fig.3 Bottom view of surface grid and space topology

2.2 螺旋桨重叠网格分布策略

在动态重叠网格中，如果遇到互相衔接的特殊情况，如螺旋桨旋转桨毂与相对静止的发动机短舱对接时，往往会因重叠网格子网格外边界的限制而将动静物面衔接处切割出一条缝隙，这样会破坏动静物面交界处的流场细节，并且缝隙内的流动变化剧烈，不利于整体流场的非定常收敛。

为了能够更好地还原流场的真实性，本文对重叠网格绘制进行特殊处理，填补上这个缝隙[22]。首先在全机背景网格中向前延伸出部分桨毂物面(统计全机气动力时并不积分这部分气动力)，如图4所示，背景网格和子网格的桨毂物面部分贴合，然后调整背景网格与子网格在重叠区域内的分布，额外将背景网格在洞边界附近单元与子网格在外边界附近单元的物面第1层高度适当放大，以保证相互之间均能找到插值贡献单元。

图4 螺旋桨处重叠网格的物面分布Fig.4 Surface mesh distribution of propeller overlap grid

2.3 典型计算状态收敛曲线

在计算非定常滑流时，首先固定螺旋桨不旋转开展定常计算，待流场收敛后，以此为初始流场再将螺旋桨按照固定转速开始非定常旋转，转速为1 075 r/min，将螺旋桨旋转一周360°视作一个周期，分成120步进行时间推进，即螺旋桨每一时间步旋转3°，在时间上采用双时间步方法，每个真实时间步内的子迭代步数为50步，采用隐式LU-SGS(Lower-Upper Symmetric Gauss-Seidel) 方法进行迭代，空间格式采用Roe通量差分分裂方法。

通过监测气动力发现通常需计算2 000步(对应螺旋桨旋转约12圈)以后，飞机的气动力开始呈周期性小幅振荡，在后处理时可以取一个周期内平均的气动力作为最终结果。对于带尾翼构型拉力系数0.4时(拉力即为螺旋桨产生的轴向力，其无因次化与飞机阻力定义一致)，来流0°迎角和0°侧滑状态的气动力收敛曲线如图5和图6所示，图中：CD、CL、Cm分别表示阻力系数、升力系数和俯仰力矩系数，CY、Cl、Cn分别表示侧力系数、滚转力矩系数和偏航力矩系数。

图5 纵向气动力/力矩收敛曲线Fig.5 Convergence curves of vertical aerodynamic force and moment

图6 横向气动力/力矩收敛曲线Fig.6 Convergence curves of horizontal aerodynamic force and moment

2.4 气动力比较

在不同拉力系数下，将计算结果与试验结果进行对比验证，试验结果在中国空气动力研究与发展中心的FL-13风洞取得，模型缩比为1∶6。对比了无动力、两种拉力系数(CT=0,0.4)的计算与试验结果，其中无动力是指将螺旋桨桨叶去掉后的定常结果，不同拉力系数通过调整螺旋桨的桨叶角与来流速度获得。按照通常定义，将螺旋桨自身产生的气动力视为直接力影响，而将螺旋桨滑流对全机产生的气动力影响称为间接影响，为分析不同拉力系数下滑流强度的干扰，下文中如无特殊说明，气动力结果均将螺旋桨的直接力影响扣除。

图7中显示了3种情形下的阻力变化曲线，从图中可以看出，计算结果整体上与试验规律一致，在迎角小于10°范围内，3种情形的偏差均较小，只有CT=0时，迎角大于10°后，计算结果略大于试验值。对比无动力与拉力系数为0两种情形，试验中阻力结果基本相同，计算中CT=0结果稍大于无动力结果，说明CT=0时螺旋桨不产生前进的拉力，并且滑流对全机的增阻效果也不显著。而CT=0.4时，滑流的增阻效果十分显著，在迎角为0°时，CT=0.4相比CT=0的阻力系数增幅达到76.7%，说明在大拉力系数下，滑流强度越强，对全机的阻力增加作用越明显，符合一般规律。

图7 无动力与不同拉力系数时阻力变化曲线Fig.7 Drag variation curves in without-power condition and with different thrust coefficients

图8中显示了3种情形下的升力变化曲线，从图中可以看出，除去失速迎角附近，在线性段范围内，本文计算方法具有较高的模拟精度，无论是量值还是曲线斜率，计算与试验的差别较小，总体上计算预测的失速迎角相比试验偏小1°～2°左右。通过对比发现，试验中CT=0时的升力系数，其结果整体小于无动力值，而在计算中CT=0时的升力系数整体上大于无动力值。在试验中由于模型缩比和电机转速等原因，模拟CT=0时采用的桨叶角为66°、前进比为6，而在计算中的桨叶角为21.15°，前进比为0.949。前进比定义为λ=V/(nD)，V为来流速度，n为螺旋桨转速，D为螺旋桨的桨盘直径。不同的桨叶角和前进比产生的滑流形态会有所不同，进而其产生的干扰和最终反应在全机气动力结果上也会不同。

图8 无动力与不同拉力系数时升力变化曲线Fig.8 Lift variation curves in without-power condition and with different thrust coefficients

图9中显示了3种情形下的俯仰力矩变化曲线，相比而言，力矩的预测结果不如阻力与升力，这是因为力矩反映了力在全机上的整体分布规律，而力反映了全机表面力的统计值，力矩精确预测的难度更大。在试验结果中，无动力和CT=0两条曲线基本重合，直到17°失速迎角后，两条曲线才开始分开。在计算结果中，迎角大于5°以后，CT=0的俯仰力矩结果明显大于无动力结果，CT=0的曲线转折点发生在16°附近，而无动力在迎角16°以后，计算曲线斜率变小，在目前20°迎角范围内，未见曲线上跷现象。对于CT=0.4情形，计算与试验均发现俯仰力矩在小迎角范围内纵向静稳定性降低现象，在试验中俯仰力矩的转折点是在1°迎角附近，计算的转折临界点没有试验明显，在[-9°,1°]迎角范围内，曲线均较平坦，在16°迎角附近，计算和试验中CT=0.4对应的俯仰力矩曲线均出现跳跃。

从上述计算与试验的纵向气动力/力矩对比可发现，在模拟工程中的实际复杂外形时，本文所采用的计算方法在有/无动力下均有较高的预测精度，能够满足螺旋桨滑流与飞机部件相互干扰的分析精度要求。

图9 无动力与不同拉力系数时俯仰力矩变化曲线Fig.9 Pitch moment variation curves in without-power condition and with different thrust coefficients

3 尾翼对螺旋桨滑流的影响

为分析有/无尾翼的影响，重新绘制无尾构型，如图10所示，机身尾段上半部分适当修形，保持光滑过渡，空间网格在有尾翼网格的基础上做适当简化即可。

图10 无尾构型外形示意图Fig.10 Sketch of without-tail-wing configuration

3.1 有/无尾翼对气动力的影响

首先对比气动力的结果，开展了最大拉力系数CT=0.4，迎角为[-6°,9°]范围内的非定常计算，此处给出的气动力不仅扣除螺旋桨直接力的影响，并且在有尾翼的结果中，还扣除尾翼的部件力，这样将其与无尾构型的结果进行比较时，能更为直观反映出尾翼的干扰作用。

图11是有/无尾翼的升力系数计算结果，发现两条曲线结果基本重合，有尾翼构型的结果稍小于无尾结果。图12和图13分别是有/无尾翼的阻力和俯仰力矩系数结果，发现有尾翼构型的阻力系数稍大于无尾翼构型，在俯仰力矩结果中有尾翼构型的曲线呈线性平移，这其中差别的原因一方面是由于两种外形下的机身后体修形不同会产生一定影响，另一方面是有尾翼构型时，尾翼的存在一定程度上会影响与其桥接的机身后体部件流场。对于典型0°迎角状态，有/无尾翼之间的升力、阻力和俯仰力矩差量分别占无尾构型结果的2.3%、3.2%和6.2%。

从以上纵向气动力/力矩结果可以初步得出，如果扣除尾翼气动力，有尾翼时的气动力规律与无尾翼基本一致，尾翼对全机气动力的影响不大。

图11 有/无尾翼带动力时升力系数对比(CT=0.4,Ma=0.15)Fig.11 Comparison of lift coefficients with and without tail wing in power state(CT=0.4,Ma=0.15)

图12 有/无尾翼带动力时阻力系数对比(CT=0.4,Ma=0.15)Fig.12 Comparison of drag coefficients with and without tail wing in power state(CT=0.4,Ma=0.15)

图13 有/无尾翼带动力时俯仰力矩系数对比Fig.13 Pitch moment coefficients contrast with and without tail wing in power state

3.2 空间速度切面云图

在0°迎角时，绘制位于左右螺旋桨轴线处的空间横向切面的速度分布云图，如图14和图15所示。虽然滑流为非定常周期性变化流场，但为表征滑流的时均掺混加速效果，图中流场结果为螺旋桨旋转一周后的平均值。

图14为右侧切面速度分布，发现来流经过螺旋桨后得到加速作用，在机翼上表面和短舱下部加速效果显著，流过襟翼后方时，由于襟翼偏转导致该部分流速降低。机翼上方加速区域经过襟翼后向下偏转，随后与短舱下方的高速气流合并为一股，从平尾下表面通过。对比无尾构型的右侧切面云图，发现仅在尾翼附近处流场有区别，尾翼下表面的气流加速效应也减弱，而远离尾翼的其他区域，二者并没有明显区别。

图15为左侧切面的速度分布，其与右侧的速度分布形态稍有不同，机翼上方的加速气流在经过襟翼后并未下偏，与襟翼后方的气流基本保持平行，并且此时加速区域离平尾下表面垂向距离更近。对比有/无尾翼的结果，发现有尾翼时，流经平尾下表面的气流由于流场的堵塞作用得到加速，而对于远离尾翼的其他区域，二者的区别仍旧不大。

图14 有/无尾翼右侧空间切面速度分布云图Fig.14 Right slice velocity distribution cloud of configurations with/without tail wing

图16为沿流动方向不同位置的切面速度分布云图，并将Ma<0.22的流动区域隐藏。从机尾朝机头看，螺旋桨是逆时针旋转，可以看出由于机翼、襟翼的干扰，滑流的加速区域被大致分割成了上下两部分，机翼上方的桨叶是朝图中左侧旋转，使得这部分气流整体往左偏转，而位于机翼下方短舱附近的气流往图中右侧偏转。正是由于右侧上半部分桨叶的滑流向左侧偏转，使得图14中右侧机翼上方的加速区域在越过襟翼后开始向下偏转。

图15 有/无尾翼左侧空间切面速度分布云图Fig.15 Left slice velocity distribution cloud of configurations with/without tail wing

图16 有/无尾翼不同流向切面的速度分布云图Fig.16 Flow direction slice velocity distribution cloud of configurations with/without tail wing

对比有/无尾翼的两幅结果，除去尾翼附近区域，发现在不同切片处，无论是速度量值，还是空间分布形态，二者差别均较小，所以从空间速度分布也印证了尾翼对滑流主流区的影响有限。

3.3 不同空间位置的下洗流和侧洗流

3.2节已经直观显示出滑流的空间形态左右不对称，其与飞机各部件干扰也具有不对称性，因此本节着重分析空间不同位置的下洗角和侧洗角变化曲线，其中下洗角定义与来流迎角类似，从机身下方来流为正；侧洗角定义与来流侧滑角类似，从机身右侧来流为正。通过空间速度的三分量可计算得出下洗角和侧洗角量值。从平尾前缘开始，向前方截取了3处位置：dx=-0.625、-0.375、-0.125，前伸距离以平尾半展长无因次化，空间切线位置如图17所示。

图18是平尾前方不同距离的空间下洗角变化曲线，横坐标以平尾半展长无因次化，即y=0对应机身对称面，y=±1对应平尾外沿。从图中可以看出左右两侧平尾前方空间的下洗角曲线分布有很大不同，左侧曲线整体上呈波浪状，大部分区域内均为下洗流，下洗角最大值在左侧平尾中部，有尾翼时下洗角能达到-20°，而右侧由机身中部的上洗向外侧逐渐转换为下洗，下洗角的最大值在最外侧。

图17 平尾前方空间监测点示意图Fig.17 Sketch of space monitor point in front of horizontal tail

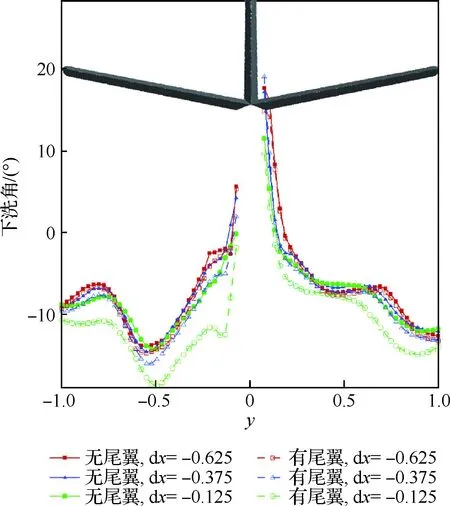
图18 平尾前方空间流场下洗角变化曲线Fig.18 Variation curves of down wash angle of flow field in front of horizontal tail

对比有/无尾翼的结果，在dx=-0.625时两条曲线基本重合，说明在该距离下尾翼对滑流区域的下洗角影响很小；在dx=-0.375时，有/无尾翼两条曲线的规律基本相同，在y=[-0.6,0]范围内，有尾翼的曲线结果整体往下平移，说明由于尾翼的阻塞作用，空间下洗角变大；在dx=-0.125时，尾翼的影响已不能忽略，左内侧带尾翼曲线往下平移均达4°以上，右外侧带尾翼曲线下移能达到3°左右。从下洗角曲线可以初步估算出，尾翼的主要影响区域在前方0.375倍尾翼半展长范围内，而对远离该区域的前方流场影响较小。

图19 平尾前方空间流场侧洗角变化曲线Fig.19 Variation curves of side wash angle of flow field in front of horizontal tail

图19是不同空间位置的侧洗角变化曲线，对于右侧平尾，前方侧洗角均为正，即该处为右前方来流，右侧平尾侧洗角为正的主要原因是右侧螺旋桨的上方桨叶产生的正侧滑，正好大范围覆盖右侧平尾。从右中部至最外侧尾翼，侧洗角均能达到10°左右。而对于左侧平尾区域，侧洗角有正有负，这是因为左侧螺旋桨的机翼下半部分桨叶产生的负侧滑会影响左侧平尾，并且随着越靠近尾翼，左外侧区域的侧洗角逐渐变大，侧洗角最小值能达到-18°。

对比有/无尾翼的侧洗角差别，发现右侧前方3种站位下的曲线基本相同；而左侧差别主要集中在y=-0.7附近，侧洗角整体差别在2°范围以内。从目前分析的几个站位结果来看，尾翼对滑流的侧洗影响较小。

3.4 不同拉力系数下的下洗流和侧洗流

在3.3节中固定拉力系数为0.4，比较了不同平尾前方空间位置的下洗角与侧洗角，本节固定前伸距离为dx=-0.375，变化不同的拉力系数，分析尾翼对滑流的影响。

图20对比了3种拉力系数下有/无尾翼时下洗角变化曲线，发现不同拉力系数下的下洗角曲线会有略微变化，在右侧3种拉力系数下的下洗角曲线差别不大，而在左侧中部y=-0.5附近，CT=0.15时对应的下洗角曲线幅值明显小于另外两种情形，说明拉力系数越大，在平尾前dx=-0.375处下洗流越强烈，符合一般规律。同时发现CT=0.34和CT=0.40的下洗曲线基本重合，说明螺旋桨在CT>0.34后，平尾前方的空间流场下洗基本相同。在不同拉力系数下，发现有/无尾翼曲线的增量基本一致，说明尾翼对平尾前方的干扰，并不会由于拉力系数的变化而产生明显差异，在目前计算的3种拉力系数下，尾翼的干扰值基本相当。

图21对比了3种拉力系数下有/无尾翼时侧洗角变化曲线，在不同拉力系数下，两侧平尾前方的侧洗角量值也是随着拉力系数增大而增大，说明拉力越大，滑流在平尾前方的侧洗效应也越强烈。进一步对比有/无尾翼的结果，发现右侧带尾翼曲线在对称面处侧洗变小，这与机身后体修形和尾翼部件的阻挡作用有关，在其余部分右侧曲线基本重合。对于左侧尾翼来说，在y=[-0.8,-0.5]范围内，有尾翼的侧洗角量值略微变大，但总体上均不超过2°范围。总体而言，不同拉力系数下尾翼对下洗角和侧洗角的干扰规律基本相同。

图20 不同拉力系数平尾前方空间流场下洗角变化曲线Fig.20 Variation curves of down wash angle of flow field in front of horizontal tail with different thrust coefficients

图21 不同拉力系数平尾前方空间流场侧洗角变化曲线Fig.21 Variation curves of side wash angle of flow field in front of horizontal tail with different thrust coefficients

4 结 论

本文对带尾翼和无尾翼两种构型的螺旋桨飞机进行了计算研究，通过对比分析探讨了尾翼对螺旋桨滑流的影响规律。

1) 将带尾翼构型的尾翼部件力扣除后，有/无尾翼的升、阻力规律基本一致，俯仰力矩呈线性平移关系，曲线平移的原因来源于机身后体修形不同和尾翼会影响与其桥接的机身后体流动。

2) 对比有/无尾翼的横向、流向空间切面的速度分布云图，无论是速度量值，还是空间分布形态，有/无尾翼的结果仅在尾翼附近有一定差别，而对远离尾翼的滑流区域差别较小。

3) 对比不同空间位置处的下洗角和侧洗角变化曲线，发现距离越近，尾翼的影响越大，在目前计算的典型状态中，前伸距离超过0.375倍尾翼半展长范围后，尾翼对空间流场的影响可以忽略。

4) 对比小、中、大3种拉力系数的空间位置的下洗角和侧洗角变化曲线，发现不同拉力系数下尾翼的干扰规律也基本一致。

5) 在飞机初期设计和选型阶段，螺旋桨滑流与尾翼的相互干扰可简化为滑流单向对尾翼产生影响，尾翼对滑流的影响可以忽略。