CFD在螺旋桨飞机滑流影响研究中的应用

马率，邱名，王建涛，缪涛，江雄

中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

螺旋桨旋转时，桨叶拨动空气，一方面使空气向后加速流动,另一方面又使空气顺着螺旋桨的旋转方向扭转流动，这种由于螺旋桨作用使气流加速和扭转的非定常复杂流动特性就是螺旋桨滑流效应。预测螺旋桨滑流对螺旋桨飞机气动特性的影响一直是螺旋桨飞机设计中亟待解决且难度很大的问题[1]。

目前,CFD方法模拟螺旋桨滑流主要分为3种方式：一种是采用由动量-叶素理论发展而来的作用盘/激励盘模型的定常方法[2-5]，一种是运用多参考坐标系(MRF)模型的准定常计算方法[6-7]，一种是基于双时间推进法的非定常数值模拟。随着计算机技术的飞速发展和计算方法的不断进步，用基于双时间推进法求解非定常雷诺平均Navier-Stokes(URANS)方程来数值模拟螺旋桨飞机滑流流场变得可行，相比于文中提到的前两种方法，求解URNAS方程能更真实地描述螺旋桨装机后桨叶旋转运动的绕流细节，滑流尾迹发生及演化的非定常过程，从而有益于研究分析螺旋桨/机身干扰流动现象及背后的影响机理。

近年来，国外已有学者开始采用非定常数值模拟方法开展螺旋桨及滑流的气动特性影响研究，例如Roosenboom和Heider[8]采用基于URNAS的DLR-TAU程序对A400M螺旋桨运输机半模的翼身组合体进行了滑流研究，并用螺旋桨转轴剖面处的涡量云图与粒子图像测速(PIV)试验结果进行了详细的流场对比，Ruiz-Calavera和Perdones-Diaz[9]分别采用试验和CFX软件对单独螺旋桨和将螺旋桨安装在飞机模型上的状态进行了对比研究。在国内，非定常数值模拟螺旋桨滑流的研究起步较晚但发展较快，许建华等[10]用URNAS方程和动态重叠网格完成了单独双桨叶模型的流场数值模拟，许和勇和叶正寅[11]对某单发简单螺旋桨飞机构型进行了URANS模拟研究，升力的计算结果高于试验值4%左右；段中喆和刘沛清[12]开展了某型螺旋桨滑流对机翼气动性能影响的数值研究；杨小川等[13]用非定常Euler方程数值模拟了螺旋桨飞机的滑流影响并进行了分析,夏贞锋[14]用动态面搭接网格技术的非定常数值模拟方法和激励盘理论研究了滑流对翼身组合体的影响及对开式转子的非定常气动特性。

以往的螺旋桨滑流影响研究往往集中在单桨的宏观气动力验证、滑流对扫过部件的气动力影响上，对于在滑流作用下的飞机部件气动力和全机稳定性分析工作还很少。本文运用自主开发的大型三维可压缩RANS方程解算器——PMBNS3D软件,数值模拟了某螺旋桨飞机巡航构型低速特性下的流动，并与试验结果进行了对比，计算值与试验值吻合，验证了程序的可靠性。并在此基础上总结了螺旋桨滑流动对飞机全机及部件气动特性和操控性能的影响规律，然后通过对螺旋桨滑流影响边界区域的定义及分析，对滑流干扰现象以及背后的物理流动机理进行了研究和探索。

1 数值方法

1.1 控制方程

在惯性坐标下，针对任意运动控制体的可压缩Navier-Stokes方程的积分形式为

(1)

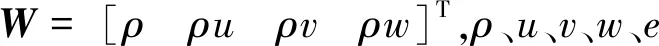
p=ρRT=ρ(γ-1)ε

(2)

(3)

式中：R为气体常数；T为开尔文温度;γ为气体等压热容与等体积热容的比值。无黏项的空间离散采用Roe平均迎风通量差分分裂格式，黏性项采用中心差分格式离散，计算分别采用了S-A一方程湍流模型和k-ω剪切应力输运(SST)二方程湍流模型。非定常计算采用双时间步方法，除了真实时间t之外，引入伪时间τ，好处是使原来只适用于定常计算的隐式时间迭代、局部时间步长、多重网格等方法都可以运用到非定常计算的伪时间迭代当中[15-16]。

1.2 多重网格方法

限制URANS非定常Navier-Stokes方程应用的一个重要因素是对计算资源的要求过高，对双时间步方法来说，提高子迭代过程的收敛速率是衡量方法的一个重要指标，而在加速方法中多重网格法被证明是最有效的手段之一[17-18]。多重网格方法的原理是利用高频误差比低频误差更容易被迭代格式消除的特点，通过引入系列逐步粗化网格的办法，将低频误差转化为高频误差，消除各种误差分量，再用套迭代技术将粗网格上的解返回到各级细网格上。多重网格法从理论上被证明至少对于线性椭圆型问题是一种最优化的数值方法，其计算工作量仅与网格节点数的一次方成正比，并且收敛速度与网格的尺度大小无关，从而特别适合应用在超大型工程数值计算问题中。本文采用了多重网格法中非线性方程的全近似格式(FAS)，套迭代技术为W循环。

1.3 动态重叠网格技术

在采用时间精确的数值方法求解中，网格运动是一个比较棘手的问题，较为成熟的方法是结构网格框架下的动态重叠网格方法[19-20]。由于不要求与各子网格共享边界，网格块之间允许重叠嵌套，从而极大降低了网格生成难度，弥补了结构网格对构型适应能力差的缺点,尤其是对于模拟螺旋桨相对机身运动的问题而言，能够充分利用重叠网格动态插值的特点，当螺旋桨运动到新的位置时，只需要在流场空间重新建立重叠关系即可。重叠网格方法的核心是首先通过“挖洞”的方式剔除流场中落在计算域外的点，然后使用插值方法完成各子网格间必要的数据通信，提供各子网格流场求解所需的内边界条件，从而实现全流场求解的匹配和耦合，它的计算主要包含以下步骤：① 重叠洞边界的确定；② 贡献单元搜索，建立插值关系。流场解算流程见图1。

本文分别对带动力全机的运动部件(桨叶及轮毂)和静止部件(全机其他部分)生成各自的网格，桨叶网格随桨叶一起运动，动态地与全机背景网格构成重叠关系，具体关系见图2，另外运动的螺旋桨网格在旋转过程中，背景网格的洞点和洞边界不会发生变化，即在运动过程中背景网格只需要搜索一次洞点和洞边界，然后在不同时刻确定洞边界点在运动部件网格中新的插值位置即可。

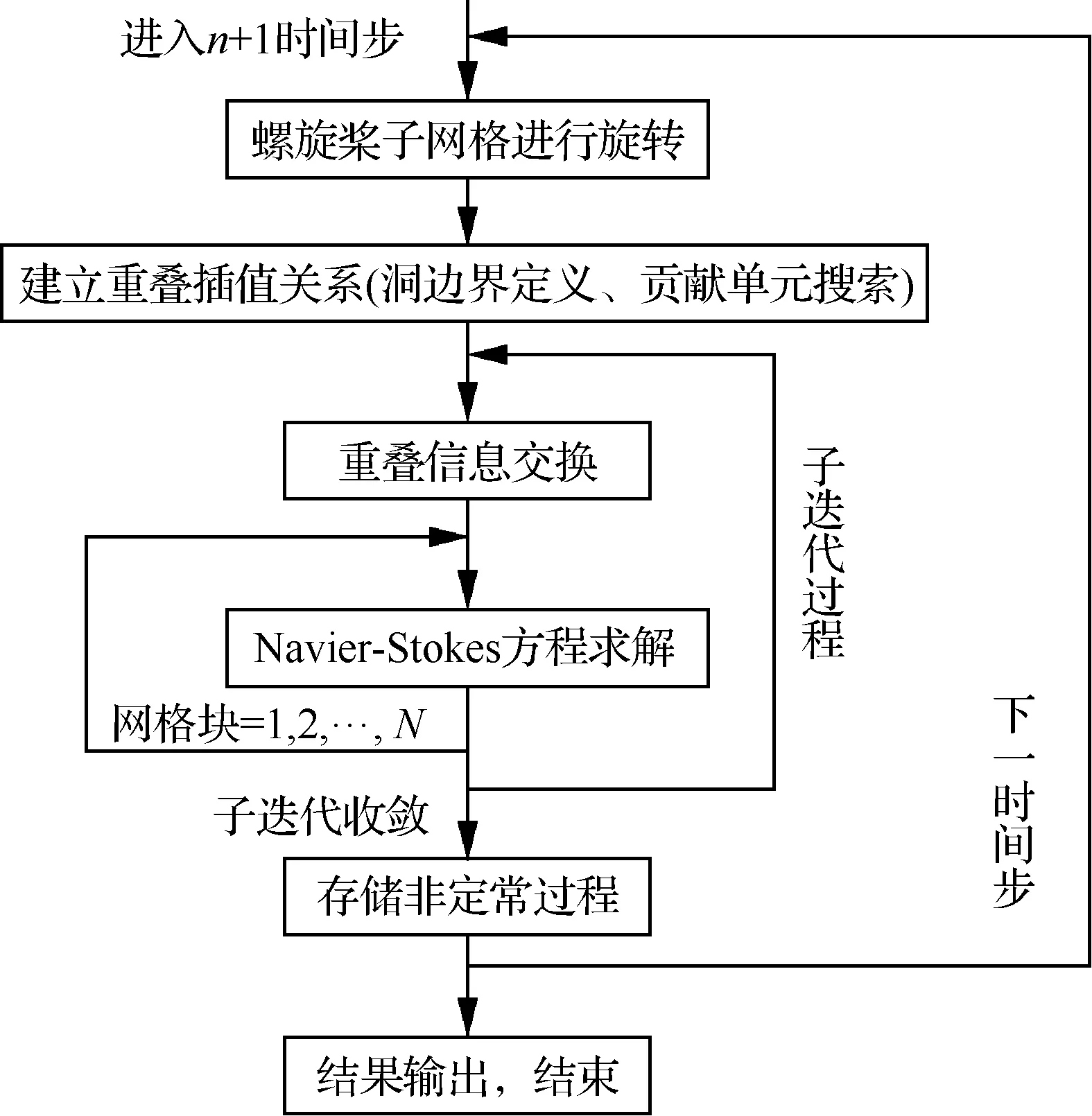
图1 动态重叠网格数值计算流程图Fig.1 Flowchart of dynamic chimera grids in numerical simulation

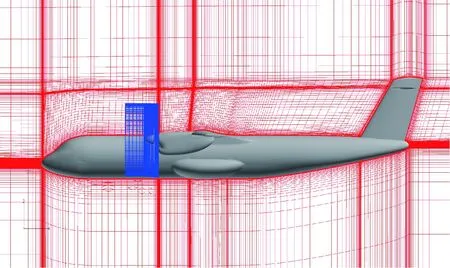
图2 桨叶网格和全机其他部分的重叠关系Fig.2 Overlapping relationship between propellers and airplane grids

1.4 并行化计算

并行计算采用基于消息传递接口(MPI)的并行化算法，用区域分割方法将计算域映射到多个CPU上分别进行计算[21-22]。利用MPI技术实现消息传递，建立了满足负载平衡的自动网格剖分方法，对隐式格式而言，每个网格块“内边界”值由相邻块处前一时刻的值来确定，对每块独立进行隐式求解，然后再根据通量守恒原理对相邻块重合点值进行修正。此外，各区块网格还可以同时采用多重网格法等技术手段来提高整体计算效益。

在并行计算之前，需要将网格比较“平均”地分配到各个计算节点上，使各节点的负载大致平衡。由于计算网格采用多块结构网格方法，在网格块数小于节点数或者现有网格分块不足以使负载平衡的情况下，对最大块进行剖分，剖分需要满足两个条件，一是沿最大维数方向进行剖分，这样保证信息交换量最少；第二要求剖分后网格满足多重网格计算条件，如果最大维数方向满足不了该条件的话就沿次大维数方向进行剖分，依次进行，按这种方法划分的网格可以在各计算节点上进行多重网格计算，提高整体计算效率[23]。在网格剖分过程中，本文将网格单元数偏差控制在7%以内，这样既能满足负载平衡的要求，同时又不会把网格分得过于零碎，增加额外的通信需求。

在发展了动态重叠网格的快速自动查询方法基础之上，实现了重叠网格挖洞、插值关系建立的完全并行化。其中找插值关系的具体过程可以描述如下：对任意插值点而言，首先在本节点查找贡献单元，在没有找到的情况下将该插值点信息发送到其余各个节点上，由这些节点同时查找该插值点的贡献单元，如果找到将该贡献单元信息返回，则建立两个节点之间的消息传递关系。这种做法的最大好处就是去掉了所谓的根节点，即任何节点的重叠网格计算不须收集网格全局信息，降低了单节点的内存要求，同时避免了单个节点计算重叠插值关系，其余节点等待的局面，提高了计算效率。

2 滑流对螺旋桨飞机宏观气动特性的影响

某螺旋桨飞机巡航无动力及带动力构型如图3所示，模型及计算的基本参数包括：模型缩比为1∶12，机翼面积为0.462 6 m2，机翼平均气动弦长为0.201 25 m，试验风速V=30 m/s，螺旋桨转速n=4 977 r/min，名义拉力系数CT=0.15，机身迎角α=-4°～20°(2°一个间隔)，机身侧滑角β=0°。

螺旋桨旋转方向为双发同向顺时针旋转(飞行员视角),为了模拟黏性附面层的需要，第1层网格距离物面的距离约为3×10-5m，满足y+=O(1)，湍流模型采用了k-ωSST二方程湍流模型。无动力全机网格采用半模的对接网格方法，网格单元总数约为1 400万，无动力全机单个定常计算状态采用16核并行计算，迭代计算20 000步取收敛结果，耗时约为24 h。

全机网格规模约3 500万，流场计算是以螺旋桨停止旋转时的定常状态作为初场，从此开始进行螺旋桨旋转的非定常计算，计算采用在惯性坐标系下求解URANS方程的方法，在时间上计算采用双时间步方法，每个真实时间步桨叶在周向运动了3°，即每个旋转周期包含真实时间步数120步，每个真实时间步内的子迭代步数为40步，采用隐式LU-SGS(Lower-Upper Symmetric Gauss-Seidel)方法进行迭代，空间格式采用Roe通量差分分裂方法。单个非定常计算状态采用64核并行计算，加速比为48，并行效率约为75%，迭代计算2 520个真实时间步数(螺旋桨旋转21转)，取一个周期内平均的气动力作为最终结果。图4给出了迎角α=0°时全机气动特性随真实时间步迭代的收敛曲线，可以看见升力系数CL在计算到约1 100步(螺旋桨旋转约9转)后呈良好的周期性化，而俯仰力矩系数Cm约1 600步(螺旋桨旋转约13转)后才收敛较好。图5给出了0°迎角下周期性建立以后的子迭代残差收敛曲线，可以看到密度残差L2模下降了近2个量级，显示了较好的子迭代收敛性。

值得一提的是，由于位于桨盘后方的飞机机翼对上游来流产生了阻挡作用，螺旋桨在对空间做功的同时，空间压力场也会对螺旋桨施加一个反作用力，这样使得安装在飞机上的螺旋桨拉力相比名义上的单桨拉力要大，本机巡航状态计算模拟得到的螺旋桨拉力系数为0.166 2，相比名义拉力系数0.15增大了10.8%，见图6。

同时扭矩系数由原来的0.080增加到了0.093，增大了约16.2%，由于扭矩的相对增幅比拉力更大一些，所以螺旋桨装机后的效率有小幅降低。图7给出的是巡航构型无动力和带动力全机低速试验和计算所得的全机气动特性随迎角的变化，需要指出的是为了和试验结果对比，图中带动力的升力系数CL和阻力系数CD曲线扣除了桨叶的直接拉力，而俯仰力矩系数Cm曲线则是加入了桨叶的俯仰力矩。从试验和计算结果的对比情况来看，升力系数在线性段的总体偏差不超过2%，在失速点附近因为机翼上出现的分离区导致计算与试验出现一些偏差；阻力系数计算结果相对试验值而言整体偏大，但偏差基本控制在8%左右，偏大原因应该来自于数值计算解的耗散行为以及采用全湍流模型带来的摩阻增加；俯仰力矩曲线趋势对比良好，在线性段带动力情况的计算值与试验值相当吻合，而在勺型区域计算值与试验值差别较大，只有带动力情况的计算值与试验值出现拐点的迎角一致；升阻比K曲线的计算结果与试验值趋势相似，但由于阻力的计算值总体偏大导致计算结果的升阻比小于试验值。

图3 全机无动力及带动力构型物面网格Fig.3 Grid of airplane surface without and with propellers

图4 全机气动特性随真实时间步的收敛曲线(α=0°)Fig.4 Convergence history of airplane’s aerodynamics characteristics vs time step (α=0°)

图5 子迭代的残差收敛曲线(α=0°)Fig.5 Convergence history of sub-iteration residual (α=0°)

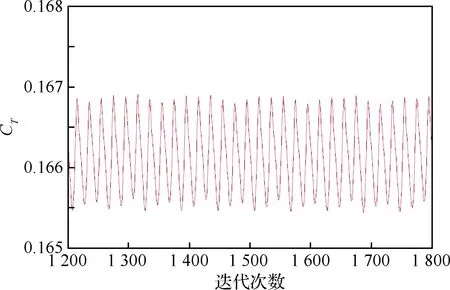
图6 计算得到的螺旋桨装机拉力系数Fig.6 Computed thrust coefficient of propeller loading on airplane

图7 全机无动力与带动力的气动特性变化(n=4 977 r/min)Fig.7 Variation of airplane’s aerodynamics characteristics (without and with propellers, n=4 977 r/min)

在滑流作用影响下，全机升力、阻力系数随着迎角的变大有明显提升，例如在迎角4°以前，升力和阻力增量变化的绝对值都不太大，但在迎角4°以后，随着迎角增大，升阻系数的增量也开始迅速放大，比如迎角12°时升力系数增幅达到19%，阻力系数增幅达到42.2%。而俯仰力矩系数斜率的绝对值小，说明带螺旋桨动力的全机俯仰安定性对比无动力有所降低。

图8给出的是对全机气动特性起主要贡献的部件随迎角的变化情况，可以看到在滑流影响下，全机升力和阻力增量主要来自机翼变化的贡献；滑流的扭转给机身和发动机吊舱带来明显的侧力影响，机身侧力的非线性导致了全机侧力在迎角增大后的振荡特性，在后面的流场分析中可以看到滑流拖出的尾涡干扰是造成部件侧力的主要原因；在不考虑螺旋桨自身的俯仰力矩情况下，全机俯仰力矩的变化主要来自于平尾和机身的贡献，在滑流影响下左右平尾产生的俯仰力矩并不对称且随着迎角的增大它们的差别也在变大。

图8 无动力和带动力全机气动特性的主要贡献部件Fig.8 Parts of main contribution in airplane’s aerodynamics characteristics(without and with propellers)

3 滑流干扰的机理分析

3.1 滑流对全机物面的影响

图9给出了无动力和带动力巡航构型随迎角变化的物面极限流线图。与无动力构型相比，由于螺旋桨的转动给气流注入了能量，在2°小迎角条件下，短舱后面的分离被抑制，从而使得逆流向分离涡明显减弱；8°迎角时短舱处流动分离区明显被抑制，整流鼓包背部的回旋涡不再对称，受到左侧螺旋桨的旋转影响被显著削弱并向右侧机翼偏移，展向分离消失；14°迎角时机翼外翼段出现了由翼梢引起的大面积展向分离，螺旋桨转动带来气流偏转效应的增强重新诱发了整流鼓包背部及右侧机翼根部的较大面积弦向分离。造成以上现象的原因经过分析认为：首先螺旋桨的转动会给气流注入能量，但同时也会带来气流的偏转效应，这样就造成了机翼上表面克服弦向逆压梯度的能力增强，即气流弦向流动分离被抑制，但气流的偏转效应造成的侧洗流场同时对机翼的展向分离带来复杂影响，这与螺旋桨的旋转方向密切相关，一般在滑流旋转与机翼翼尖涡方向同一侧时，机翼的展向分离会有所提前，反之，会推迟机翼展向分离。

由于低速迎角2°为典型状态，下面对该状态进行细节上的分析，图10给出了低速巡航迎角2°时无动力及带动力机翼的弦向截面站位压力系数，由于螺旋桨的转动给气流注入了能量，滑流区域机翼上的动压和静压都有所增加，在图10中表现为驻点压力增加，即压力系数的正峰值明显超过1而大于无滑流状态；其次，由于气流的旋转，滑流区域机翼上的局部迎角发生显著改变，滑流对短舱对称两边机翼剖面的当地气流迎角的影响作用也是不同的，反映在飞机前视图中可以看到机翼前缘压力在吊舱两侧出现了明显的不同变化。参照图10中对称于吊舱两边的截面站位压力系数比较，在桨叶上行一侧Y=3 240，-5 500 mm处，机翼前缘的吸力峰在螺旋桨滑流影响作用下明显增大，这对提升机翼的升力和减小阻力带来了有利影响，但是在桨叶下行一侧Y=5 500，-3 240 mm处，机翼前缘的吸力峰消失甚至在下翼面出现负压力值(图中机翼弦向站位x/c≈0～0.15处属于向下压力峰的作用范围)，该处会抵消动压升高对这部分机翼升力的作用。

图9 全机巡航状态物面压力系数和极限流线随迎角变化情况(无动力和带动力)Fig.9 Pressure coefficients and streamlines on cruise state airplane’s surface vs angle of attack (without and with propellers)

图11反映的是无动力及带动力机翼的展向截面站位压力系数，η为展向站位系数可以发现在机翼的前缘位置，滑流对当地的压力系数有着非常明显的改变，而随着流动在弦向的发展，螺旋桨滑流对机翼的影响沿展向是逐渐减弱的，在机翼后缘位置附近时，展向上的压力分布除了在吊舱位置有所不同外，其他地方的分布与无动力状态相似。

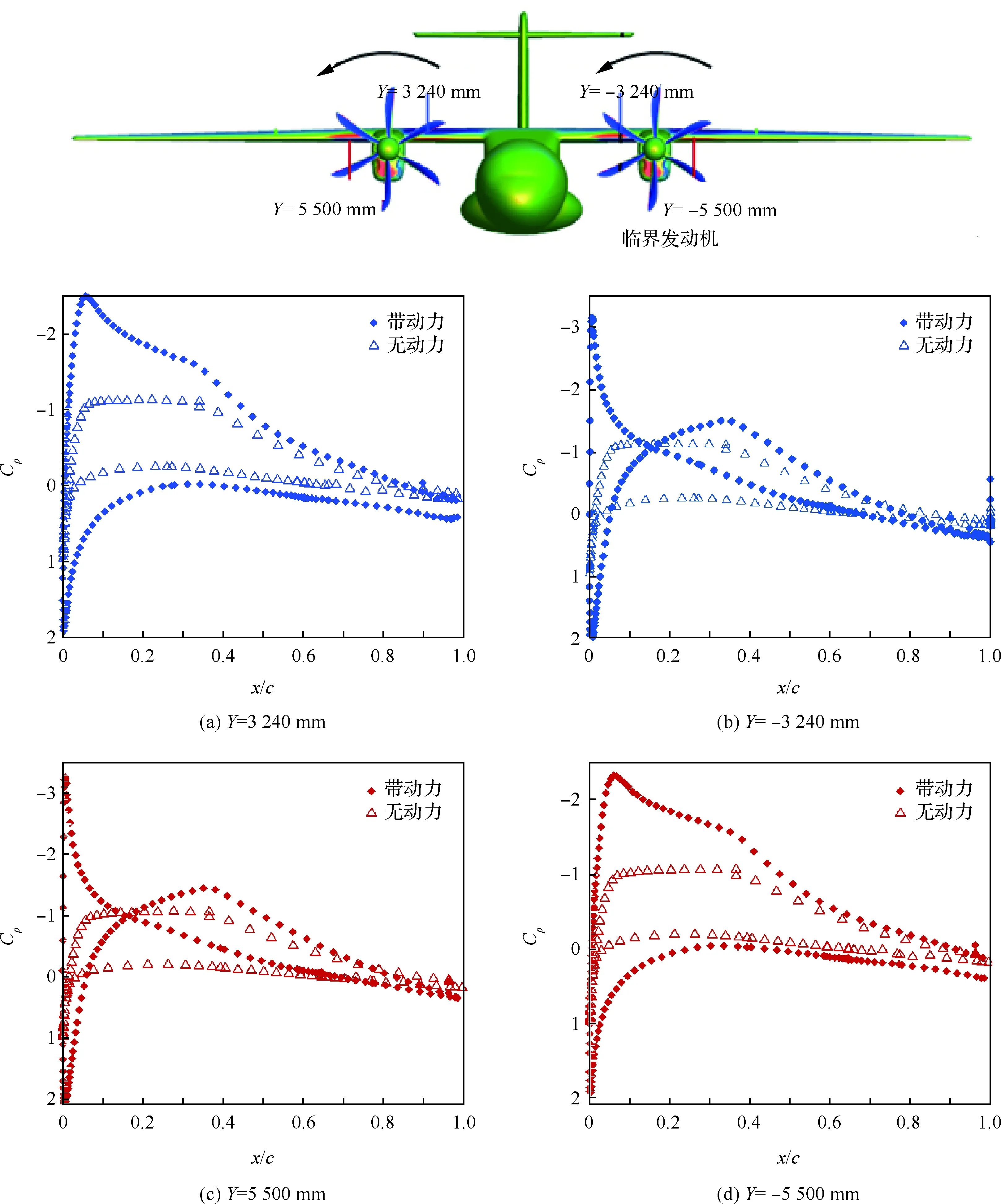
图10 全机无动力和带动力不同机翼弦向站位的压力系数分布(Ma=0.008,α=2°,CT=0.15)Fig.10 Cp distributions for different stations located on wing chordwise (without and with propellers Ma=0.008,α=2°,CT=0.15)

图11 全机无动力和带动力不同机翼展向站位的压力系数分布(α=2°)Fig.11 Cpdistributions for different stations located on wingspan direction(without and with propellers, α=2°)

3.2 滑流对空间流场的影响

图13给出的是螺旋桨转轴位置Y=-4 370 mm处的弦向剖面的Q值云图，可以看到螺旋桨桨叶卷起的尾迹涡和由轮毂和发动机吊舱产生的涡结构，桨叶的尾迹涡随尾迹圈数的增加，旋涡直径增大，旋涡强度减弱，而发动机短舱产生的涡从物面脱出后呈狭长的条状带，尤其是下翼面吊舱后部的分离涡强度大且贯穿到了机身尾部。

图12 带动力巡航状态空间涡量等值面Cp图Fig.12 Iso-surfaces of Q-criterion colored by Cp on cruise state with propellers

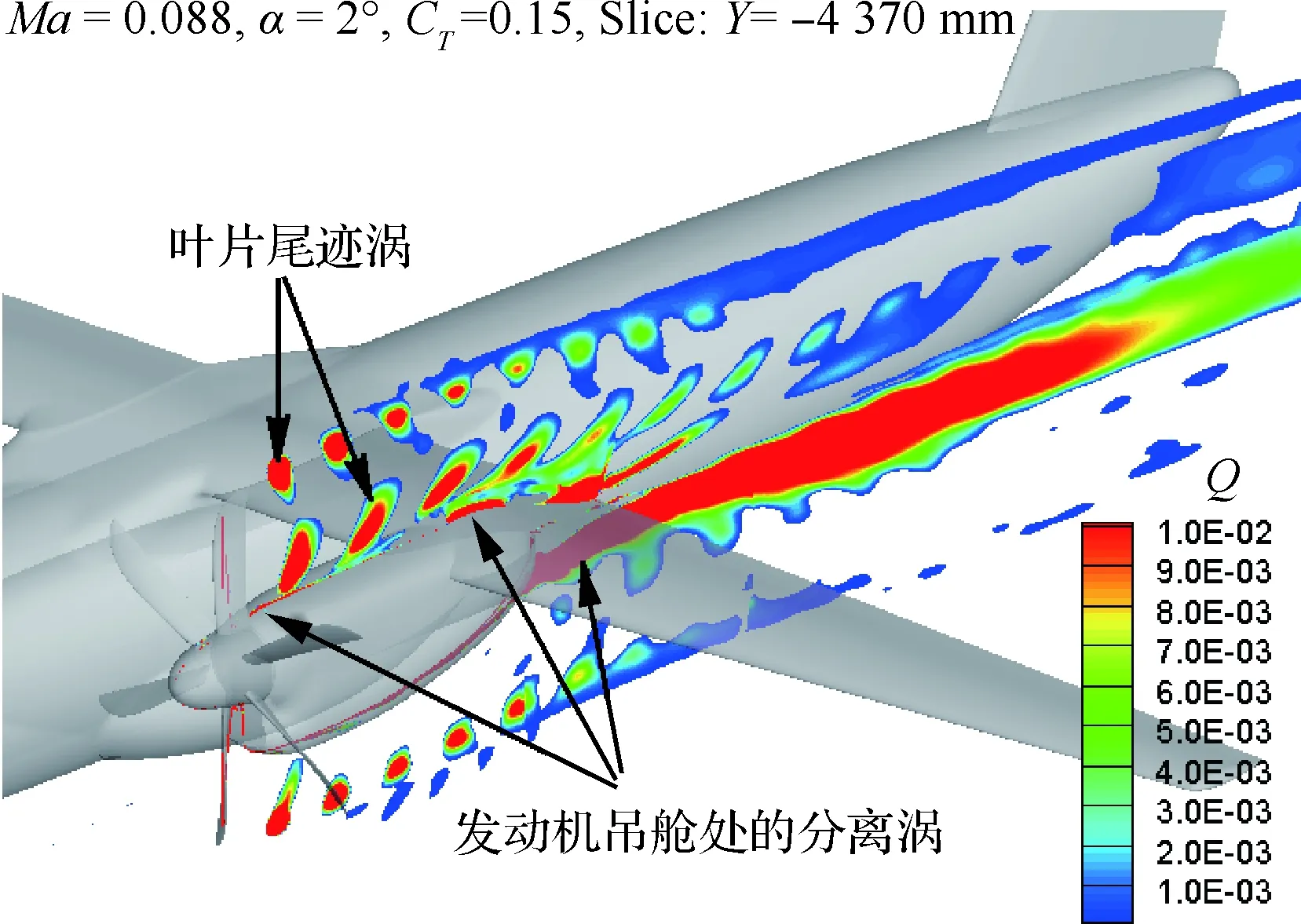
图13 螺旋桨转轴位置弦向剖面的涡量分布Fig.13 Vorticity contour at propeller rotation axis chordwise

在飞机开始设计阶段就需要考虑螺旋桨滑流对扫过飞机的气动操纵面的影响，最好能避开滑流影响区域，如确实无法避免则需迫切知道滑流对当地流场的影响。但由于滑流和射流相似，在空间发展过程中不断与周围空气相混合，并受到黏性耗散，使得滑流向外扩散减速并不断“模糊”其边界，滑流流管沿流向发展的巨大畸变对滑流影响的分析工作带来了巨大困难。水平尾翼如果部分或完全浸没在螺旋桨滑流中，会承受较高的动压，从加速作用的角度来看，这会增大尾翼有效升力线斜率，加强尾翼对稳定性的贡献；同时螺旋桨桨叶的旋转对流场带来了洗流的作用——不限于滑流的流管，而是近似遍及整个流场，压强分布(以及随之的气动力和力矩)与无滑流时有很大的不同。图14～图16分别给出了不考虑螺旋桨自身力矩情况下，有/无动力的全机在2°迎角时各部件的力矩系数贡献图,可以看到在滑流影响下，机翼和吊舱存在低头力矩，而机身和右侧平尾存在明显的抬头力矩，左右平尾俯仰力矩差别巨大的原因是由于滑流对它们产生了明显的不对称下洗作用，此时平尾对飞机纵向稳定性的贡献是下降的；飞机的左偏航力矩贡献主要来自机身和立尾，左右吊舱和机翼的偏航力矩各自反向近似抵消；全机的滚转力矩主要来自于飞机左右机翼滚转力矩的不对称性，由于螺旋桨同向旋转的原因，机翼升力偏置导致左侧机翼升力相对于飞机重心的力臂距离比右侧机翼升力更长，这样即使在左右机翼升力相近的情况下,左侧机翼产生的滚转力矩自然会更大，可见滑流使飞机部件的气动特性明显复杂化。

图14 无动力和带动力的部件俯仰力矩系数贡献(α=2°)Fig.14 Parts contribution in airplane’s Cm (without and with propellers, α=2°)

图15 无动力和带动力的部件偏航力矩系数贡献(α=2°)Fig.15 Parts contribution in airplane’sCn (without and with propellers, α=2°)

图16 无动力和带动力的部件滚转力矩系数贡献(α=2°)Fig.16 Parts contribution in airplane’s Cl (without and with propellers, α=2°)

本节前文中曾分析到滑流对流场的影响主要是来自加速作用和洗流,并且滑流为非定常的周期性变化流场，为了研究滑流的周期时均影响效果，本文采用有/无滑流不同情况下对比当地动压增量来定义滑流的加速效应边界，对比当地气流角增量来定义滑流的洗流效应边界，期望通过对滑流起主要影响作用的参数分解来判定滑流的影响区域。为了达到以上目的，需要将螺旋桨停止旋转时定常状态的流场和螺旋桨正常旋转的非定常滑流的周期时均流场进行对比，得到两者间的加速作用和洗流的增量变化。图17～图19分别给出的是在滑流影响作用下，空间流场不同截面的动压增量Δq、当地迎角增量Δα和当地侧滑角增量Δβ的变化情况。

图17中的动压增量Δq为无量纲量,可以发现空间中除桨叶卷出的滑流流管以外的地方动压增量Δq近似为0，流管中机翼上下翼面附近处的动压增量达到0.004左右，相比流场远处来流的动压q增加了一倍以上(远场来流动压q=0.003 87)，动压的变化在向下游发展的过程中逐步减弱，由于飞机采用T尾布局形式，远离了动压剧烈变化区域，动压变化对平尾位置没有明显的影响。图18给出的是有/无滑流情况下当地气流迎角增量Δα的空间剖面图，可以明确看到滑流在空间上下洗流的影响情况，在桨叶后方的机翼吊舱两侧，桨叶上行侧的Δα=7°～15°，下行侧的Δα=-5°～-14°，而当流动经过机翼后，机翼后方的绝大部分区域下洗被明显增强，只有位于桨叶上行侧的机翼下表面后方区域有较大的上洗，而在空间流场中的平尾前方区域可以看到右侧平尾的前方有约-2°左右的下洗增量，左侧平尾的前方却有约0.5°左右的上洗增量，这就导致了前文中提到的左右平尾俯仰力矩差别巨大的现象，同时右侧平尾产生明显的抬头力矩，导致飞机纵向静安定度下降。图19反映的是有/无滑流情况下当地气流侧滑角增量Δβ的空间剖面图，能够看到滑流对空间流场侧洗的影响，对于顺时针旋转的螺旋桨，机翼上面的滑流向右偏斜，下面滑流向左偏斜，在机翼后汇合起来，一般在机翼上仍近似圆形，离机翼后缘越远，畸变越大，而立尾上左右侧面Δβ在-5°～5°范围呈不对称变化，最终导致立尾有较大的右向侧力和左偏航力矩。

图17 带动力巡航状态动压增量变化的空间剖面图(α=2°)Fig.17 Incremental of dynamic pressure for different sections in flow field on cruise state with propellers (α=2°)

图18 带动力巡航状态当地迎角增量变化的空间剖面图(α=2°)Fig.18 Incremental of local angle of attack for different sections in flow field on cruise state with propellers (α=2°)

图19 带动力巡航状态当地侧滑角增量变化的空间剖面图(α=2°)Fig.19 Incremental of local angle of sideslip for different sections in flow field on cruise state with propellers (α=2°)

4 结 论

对有/无滑流影响作用的某双发同向旋转螺旋桨飞机进行了巡航构型低速状态的数值模拟，与试验结果进行了对比,并对滑流的影响作用开展了详细的分析，得到了以下结论：

1) 在现有计算条件下，线性段范围内升力系数与试验数据的误差能控制在2%左右，阻力系数计算结果相对试验值偏大，但误差能基本控制在8%左右，俯仰力矩曲线在线性段与试验值趋势一致，但在勺型区域开始与试验值有较大偏差。

2) 从宏观的气动力特性来看，在不计入桨叶直接气动力情况下，受滑流影响的全机升力系数、阻力系数有明显提升，它们主要来自机翼变化的贡献，且随着迎角的变大，升、阻系数的增量也开始放大；俯仰力矩的变化主要来自于平尾和机身的贡献，左右平尾俯仰力矩呈现巨大的不对称性，全机俯仰力矩系数斜率的绝对值减小；同向旋转的滑流不对称性使机身和立尾产生了明显的附加偏航力矩,使机翼产生了附加的滚转力矩。由于非对称滑流带来的非对称气动力，飞机的操纵效能相比无动力时严重下降，这就要求飞机在飞行过程中要不停调整各操纵面进行气动力补偿。

3) 螺旋桨后拖出的滑流改变了机翼的流态，其影响大致可以分为两个方面：首先增加了滑流区机翼上的动压，产生了一个升力增量和诱导阻力增量；其次改变了机翼上的局部迎角，使滑流区内螺旋桨上行桨叶侧有效迎角增大(相当于诱导出一个机翼正弯度)，从而在机翼上诱导出一个正升力增量，同理滑流区内螺旋桨下行桨叶侧有效迎角减小(诱导出一个机翼负弯度)，该处会抵消动压升高对这部分机翼升力的作用。

4) 螺旋桨滑流对飞机机翼的失速影响也非常复杂。概括来说，首先螺旋桨的转动会给气流注入能量，这样就造成了机翼上表面克服弦向逆压梯度的能力增强，即气流弦向流动分离被抑制，但螺旋桨也会带来气流的偏转效应，它造成的侧洗流场会对机翼的展向分离带来复杂影响，这与螺旋桨的旋转方向密切相关，一般在滑流旋转与机翼翼尖涡方向同一侧，机翼的展向分离会有所提前，反之，会推迟机翼展向分离的出现。

5) 本文采用有/无滑流不同情况下对比当地动压增量和当地气流角增量来定义滑流的加速效应和洗流效应边界，采用该方法能较好地捕捉和解释由于滑流对飞机尾翼干扰而使得飞机方向安定性呈现的很大非线性现象，增进了滑流对扫过飞机部件的气动干扰作用机理的认识。

致 谢

感谢中航工业第一飞机设计研究院许瑞飞给予的帮助。