立式捏合机桨叶型面设计与优化①
詹小斌,李锡文,张嘉琪,崔 峰
(1.华中科技大学 机械科学与工程学院,武汉 430074;2.湖北三江航天江河化工科技有限公司,宜昌 444200)
0 引言
立式捏合机是固体推进剂生产的关键设备,其产品质量和生产效率与桨叶结构密切相关[1-3]。桨叶结构主要由桨叶高度、螺旋角和型面决定[5]。航天四院42所王正方等进行了桨叶型面的基础研究,给出了桨叶参数的基本关系[4]。华中科技大学易朋兴等对桨叶的螺旋角进行了研究,设计了桨叶建模和优化系统,得出了具有最佳混合性能的螺旋角范围[5-6]。高粘度物料混合流场的计算流体力学(CFD)分析也逐渐成熟,并已用于优化混合设备的关键结构和工艺参数[7-10]。这些研究成果对提高固体推进剂混合效果具有非常重要的意义。
现有文献对桨叶捏合原理及桨叶型面的研究很少,少有指导桨叶设计的研究成果和理论。本文首次依据桨叶的捏合原理,通过分析桨叶运动特性、仿真桨叶捏合过程,修正了空心桨叶的捏合面轮廓;通过分析桨叶的力学性能和非捏合面的建模区域,提出了实心桨叶非捏合面轮廓的设计方法,并进行了有限元验证。
1 立式捏合机工作原理
立式捏合机为行星齿轮双桨形式,2个桨叶在混合容器绕各自轴线自转,并绕混合容器中心公转。在桨叶与桨叶之间、桨叶与混合容器壁之间满足最小间隙要求。通过自转和公转运动形成高剪切力,促使固体推进剂均匀混合,桨叶外形及位置关系如图1所示。
本文以1 L立式捏合机桨叶设计为实例,桨叶型面的主要几何尺寸如图2所示。桨叶的设计参数为:混合容器直径D=120 mm,桨叶高度h=90 mm,桨叶外径d=60 mm,基圆直径db=19 mm,桨叶间隙e=(2.2±0.1 mm),实心桨叶偏心距as=13.9 mm,空心桨叶偏心距ak=27.8 mm,两桨叶中心距a=as+ak=41.7 mm,初始捏合角β= 45.695 5°,空心桨叶与实心桨叶的转速比为iks=2。
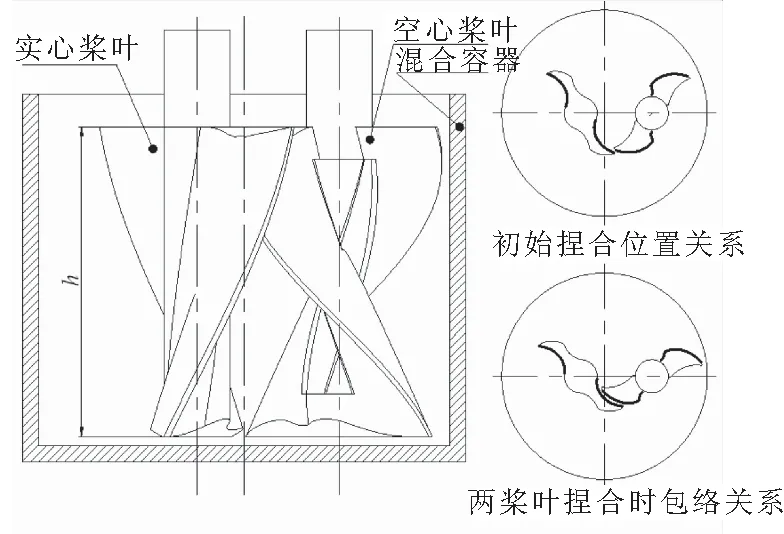
图1 桨叶外形及位置关系

图2 桨叶型面的主要几何尺寸
2 空心桨叶捏合面修正
2.1 桨叶捏合面设计原理
根据捏合原理,桨叶尖点的运动轨迹距另一桨叶捏合面轮廓的最小距离为e。在设计实心桨叶捏合面时,额外地为两桨叶捏合系统添加一个与实心桨叶运动方向相反、转速相等的运动,使实心桨叶转速为0,空心桨叶做复合运动以保持与实心桨叶的相对运动关系不变,如图3(a)所示。P1P2为过空心桨叶两尖点的直径向外延伸2e所得,x2O2y2绕O1以ws转动,P1P2绕O2以wk转动,从初始捏合位置开始至与基圆相交的P1点运动轨迹即为实心桨叶的捏合型面。计算空心桨叶捏合面时,现有文献都采用了同样方法[4,6,9]。
2.2 空心桨叶捏合面的设计缺陷
在计算实心桨叶时,空心桨叶尖点处于实心桨叶的包络范围内,空心桨叶直径向外部延伸2e,与实心桨叶捏合面轮廓相交,处于正常捏合状态。但当以实心桨叶尖点向外延伸2e计算空心桨叶型面时,计算起点P3与实心桨叶的尖点不重合,如图3(b)所示。
对比图3(a)、(b),计算空心桨叶时,改变了以下实际捏合条件:
(1)桨叶的初始捏合角;
(2)空心桨叶与实心桨叶的包络关系;
(3)两桨叶的相对位置关系。
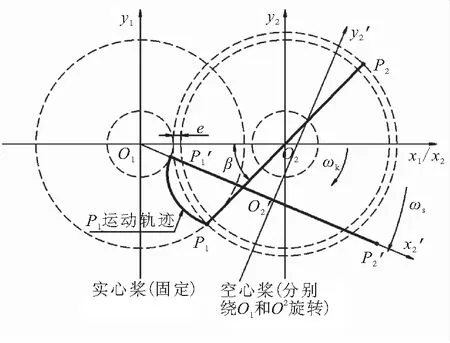
(a)实心桨叶
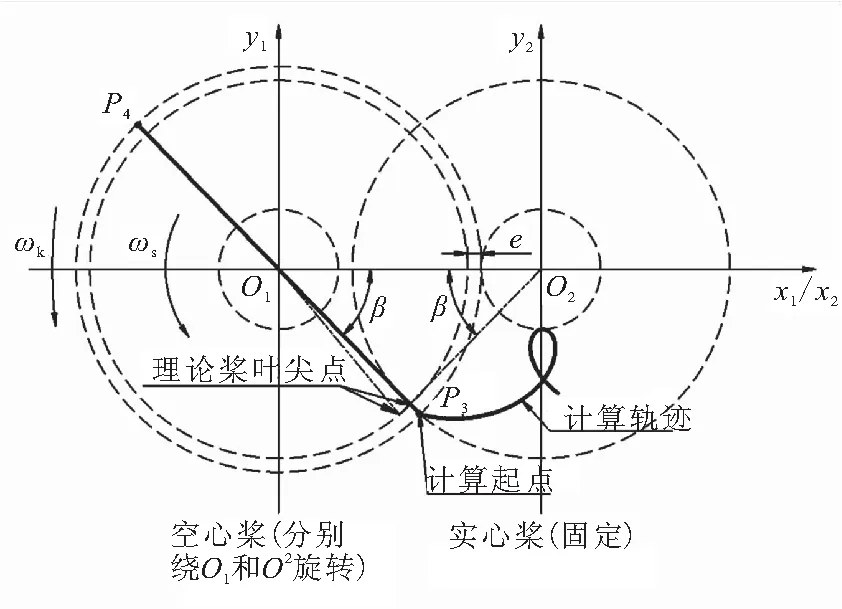
(b)空心桨叶
2.3 空心桨叶捏合面的数学模型
根据捏合要求,一个桨叶尖点的扫掠轨迹与另一个桨叶的型面最小间隙为e。因此,可先求出实心桨叶尖点的运动轨迹,然后将该轨迹向外侧法向偏移e,得到一条与该轨迹距离为e的等距曲线,即为空心桨叶捏合面轮廓。计算过程如图4所示,其空心桨叶捏合面轮廓的数学模型可表示为
Ck(θ2)=G(θ2)+e·N(θ2)
其中,G(θ2)=(xk(θ2),yk(θ2))为实心桨叶捏合尖点的运动轨迹,由下列方程确定:
式中θ2为空心桨叶完成一次捏合的自转角位移。
N(θ2)为G(θ2)的指向外侧的单位法向量:
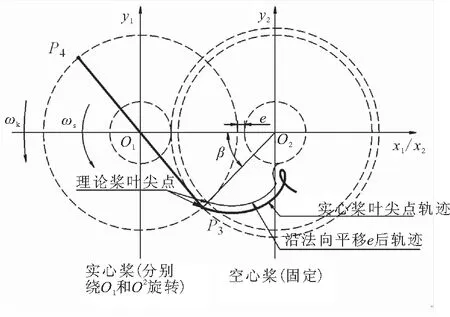
图4 修正后空心桨叶轮廓生成示意图
2.4 桨叶轮廓仿真
通过Matlab仿真运动过程,修正后的空心桨叶型面在多个方面得到改善,表现在:
(1)在整个捏合过程中,都保持与实心桨叶尖点的运动轨迹等距,从而减小了混合死区;
(2)修正前捏合长度为21.79 mm,修正后捏合长度为31.78 mm,捏合范围增加约31.5%,从而提高了捏合效率;
(3)减小了桨叶根部的应力集中。
轮廓对比如图5所示。
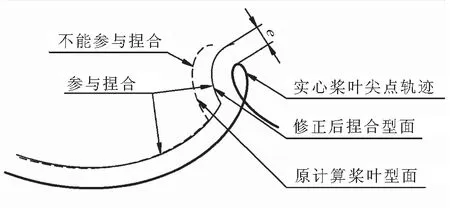
图5 修正前后空心桨叶捏合轮廓对比
3 实心桨叶非捏合面优化
在混合过程中,桨叶的一侧为捏合面,另一侧为非捏合面。非捏合面不直接影响产品质量,但非捏合面必须满足以下要求:(1)与另一桨叶运动轨迹最小距离不小于e;(2)满足桨叶的强度和刚度要求;(3)桨叶的体积(质量)越小越好;(4)过渡光滑平缓。
3.1 非捏合面的建模区域
根据桨叶的捏合原理,固定一个桨叶,另一桨叶做复合运动,以保证2个桨叶的相对运动关系不变,运动桨叶运动一个周期后,运动桨叶两个尖点在整个工作区的扫掠轨迹内侧为运动桨叶覆盖区,扫掠轨迹外侧且与其距离为e的等距曲线,在固定桨叶外圆与基圆之间包围的区域为固定桨叶的建模区域,如图6中剖面线所示。因此,在建模区域内进行非捏合面设计,能保证与另一桨叶任何位置的最小距离不小于e。空心桨叶非捏合面建模区域大,限制因素少,可按相同原理进行设计,本文不做具体讨论。
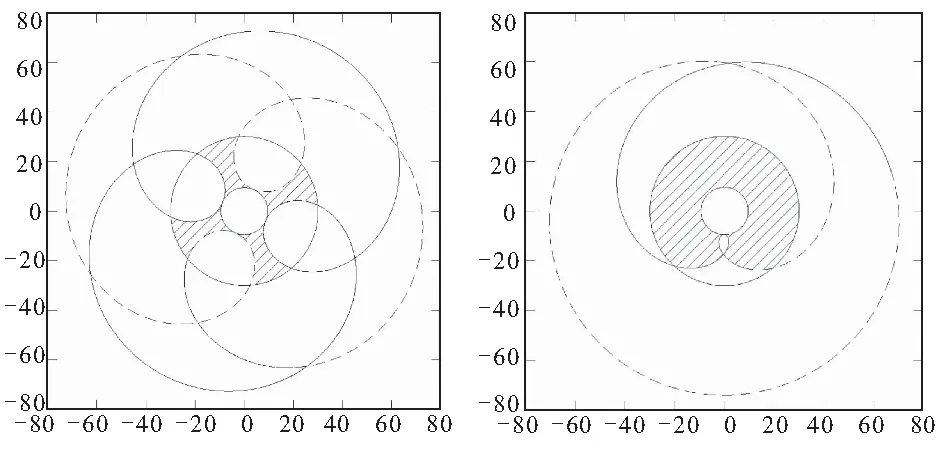
(a)实心桨叶建模区 (b)空心桨叶建模区
3.2 实心桨叶的受力分析
桨叶在混合过程中对物料挤压和剪切,受到物料产生的垂直于桨叶表面的挤压力Fj和与桨叶表面相切的剪切力Fq。挤压力Fj可分解为垂直于桨叶型面的法向力Fn(用线载荷q(x)表示)、切于桨叶型面轮廓的切向力Ft和沿桨叶主轴方向的轴向力Fa。实心桨叶某一型面受力如图7所示。桨叶表面的受力大小可通过流体分析软件计算得来,目前已有诸多研究成果[9,11-12]。
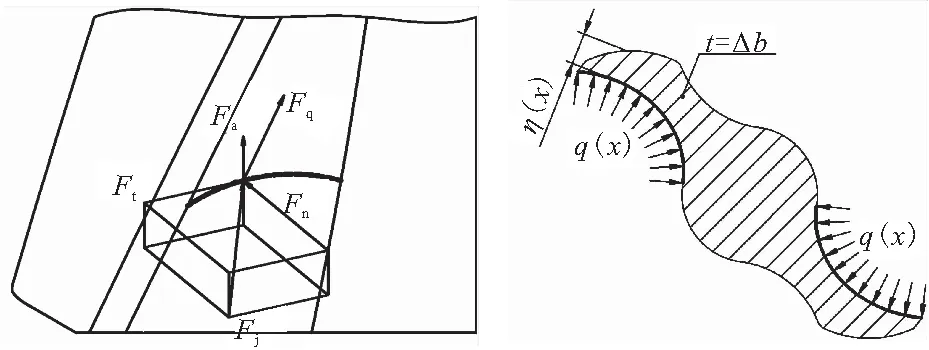
(a)桨叶受力情况 (b)法向力分布
由于影响桨叶型面刚度和强度的主要因素是法向力,故计算时忽略其他作用力,并设定捏合面线载荷为均布载荷q。由于只考虑桨叶的法向力,为了简化设计过程,从桨叶中取出厚度为b(极小)的一段桨叶,将桨叶展开为悬臂结构来计算弯矩和剪切力,如图9所示。弯矩可表示为
根据等强度原则,可使桨叶的抗弯系数随弯矩变化,修去不必要的型面。桨叶抗弯系数沿轮廓方向的变化规律为
从而,桨叶型面宽度应满足:
(1)
桨叶的等剪切强度设计条件为
从而,其桨叶型面宽度应满足:
(2)
因此,桨叶型面宽度η(x)为
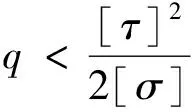
式中l为桨叶捏合轮廓展开总长度,l(x)为桨叶捏合轮廓距离桨叶中心的距离;η(x)为桨叶截面方向的厚度,见图7和图8。
根据式(1)和式(2)可知,桨叶型面的宽度呈线性关系,最大宽度位于桨叶的起始段,最小宽度位于桨尖。
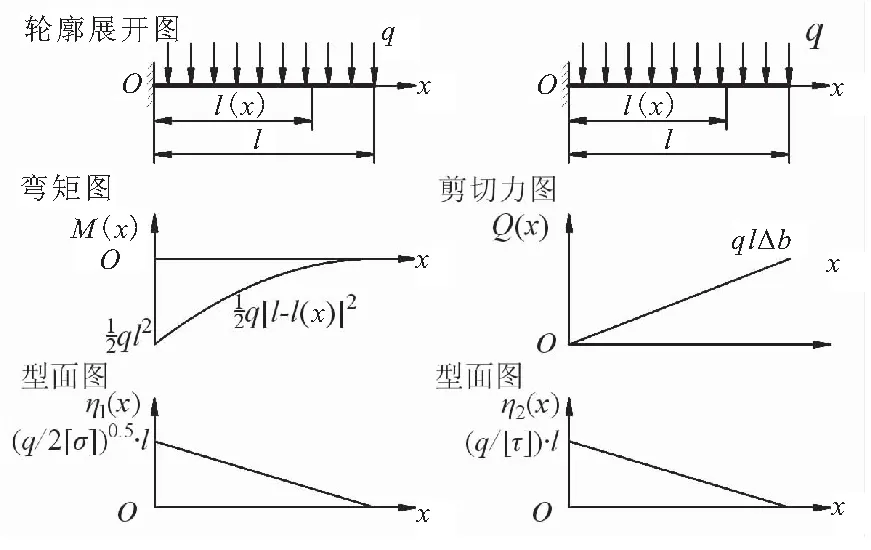
图8 实心桨叶弯矩和剪切力分析
3.3 实心桨叶非捏合面设计
根据混合物料的不同,桨叶捏合面的压力p不同,计算的η(x)也不同。为保证混合的可靠性,可按桨叶的最大强度来设计,即以建模最小距离(薄弱点)为一设计定值,然后按照η(x)∝x来确定完整的非捏合面间隙。如图9所示,将非捏合面以建模最小距离分为两段,近桨段所受弯矩和剪切力都较大,其型面宽度应较大,极限情况可取建模区域边界。对于远桨段,弯矩和剪切力都逐渐变小。因此,型面宽度也应随轮廓位置逐渐减小,其最小值为ηmin。图9中采用等分方法,保证相同Δx减少相应的Δη(x),图中仅粗略地给出了远心段的非捏合面轮廓设计原理,而更精准地设计可通过增加控制点或通过matlab等软件计算实现。
与捏合轮廓呈线性关系的轮廓也是样条曲线,考虑结构简单、型面光滑平缓和参数化建模等要求,使用圆弧来拟合非捏合轮廓。如图10所示,在近桨段,轨迹与基圆相切。因此,替代圆弧与桨叶基圆相切、半径不小于捏合曲线的曲率半径,即可满足不干涉条件。远桨段取两个端点和中间点拟合为圆弧即可,其拟合误差不大于0.05 mm。如图10所示,pn为非捏合面轮廓典型点;o1p1为非捏合面轮廓垂线;o3为p1p2垂直平分线与o1p1交点,即为替代圆弧圆心。
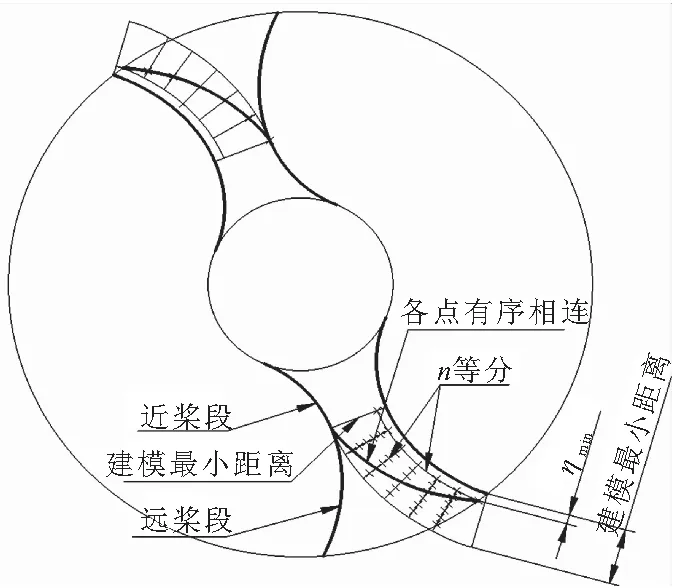
图9 非捏合面轮廓设计

图10 非捏合面轮廓优化
3.4 实心桨叶的有限元验证
3.4.1 力学分析验证
将桨叶的型面按照梁模型计算,其受压力p=2 kPa,其弯矩和剪力分布如图11所示。可见,与前面实心桨叶的受力分析吻合。分析弯矩和剪力数据与位置的关系可知,弯矩图与桨叶位置关系呈2次多项式关系,剪切力与桨叶位置关系呈线性关系。
(a)弯矩分布图 (b)剪力分布
3.4.2 应力应变验证
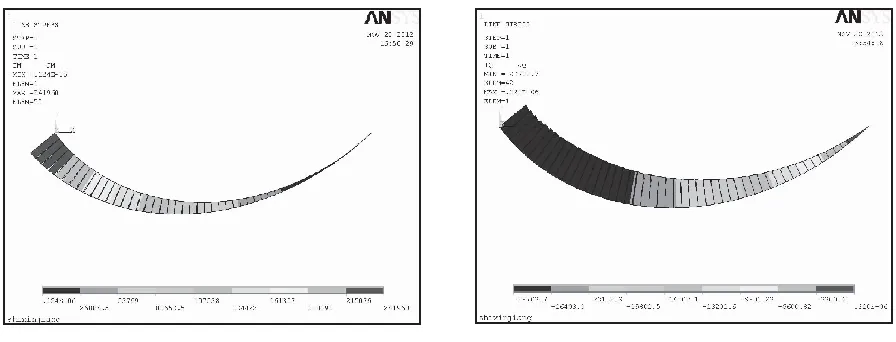
将优化前后的桨叶模型进行有限元分析,计算环境为面压力p=2 kPa,材料参数E=2.06 Pa,ν=0.3。优化前后的Von Mises云图如图12所示,其数据对比见表1。从优化前后的VonMises stress云图可知,优化后的桨叶应力集中区域减少,应力变化趋于平缓。对比ANSYS数据可知,优化后桨叶变形减小3%,体积缩
小约2%,而正应力分布和切应力变窄了,最大正应力为优化前的79.9%,最大切应力为优化前的81.3%。

(a)优化前的VonMises stress云图

(b)优化后的VonMises stress云图

项目最大变形/m最小正应力/Pa最大正应力/Pa桨叶体积/mm3XY面最小负切应力/PaXY面最大正切应力/Pa优化前0.201×10-4547.81956 431.445 459-25 777.429 696.2优化后0.195×10-4678.62845 085.644 647-19 097.124 147.4优化后/优化前/%97.0123.979.998.274.181.3
4 结论
(1)依照捏合原理,通过建模分析、运动特性仿真和力学性能分析,研究了立式捏合机桨叶的型面,提出了桨叶型面新的设计方法。新设计方法已在1 L、3 L和5 L立式捏合机上应用,对桨叶的混合性能和力学性能有较大改善。
(2)空心桨叶捏合型面模型修正。根据捏合原理,分析了现有空心桨叶计算过程,找出了存在的问题,提出了空心桨叶建模的新方法。仿真结果表明,捏合范围提高了约31.5%。
(3)实心桨叶的非捏合面轮廓优化。根据捏合要求,对实心桨叶的非捏合面进行系统分析,提出了基于等力学性能的最大承载能力的非捏合面轮廓设计方法。ANSYS仿真结果表明,优化后的桨叶在变形减少情况下,最大正应力和最大切应力都减小了约20%。
参考文献:
[1] Tanguy P A,Thibault F,Dubois C,et al.Mixing hydrodynamics in a double planetary mixer[J].Chemical Engineering Research and Design,1999,77(4):318-324.
[2] 杨明金.立式捏合机混合釜内固体推进剂药浆混合的研究[D].武汉:华中科技大学,2008.
[3] Davens A.Development of modern solid propellants[J].Journal of Propulsion and Power,2003,19(6):1108-1128.
[4] 王正方,翟瑞清.立式捏合机搅拌桨的设计[J].固体火箭技术,1993(1):65-69.
[5] 易朋兴,崔峰,胡友民,等.立式捏合机搅拌桨螺旋角影响数值分析[J].固体火箭技术,2008(4):381-385.
[6] 易朋兴,刘世元,崔峰,等.基于流场模拟的复杂形面搅拌桨叶三维设计与优化系统[J].宇航学报,2009(1):321-326.
[7] Yi P,Hu Y,Liu S.Numerical investigation of effect of stirring blades on mixing efficiency of a planetary kneading mixer with nonewtonian and viscoplastic materials[C]//AIP Conference Proceedings,2008.
[8] Liu B,Liu X J,Zhao Z Y,et al.Strength analysis of 2 000 L-B vertical mixer blades with FEM[J].Key Engineering Materials,2010,426:308-311.
[9] 易朋兴.立式捏合机设计研究与性能分析[D].武汉:华中科技大学,2007.
[10] Heniche M,Tanguy P A,Reeder M F,et al.Numerical investigation of blade shape in static mixing[J].AIChE Journal,2005,51(1):44-58.
[11] 关英波.立式捏合机搅拌桨叶的力学数值分析[D].武汉:华中科技大学,2007.
[12] 赵汝岩,邹常青.捏合机桨叶搅拌过程受力分析[J].海军航空工程学院学报,2011,26(4):572-575.

