探究奇偶旋翼对雷达回波的影响
陈尹翔 张 军 罗才震 孙慧敏
(西安电子工程研究所 西安 710100)
0 引言
在现代战争中,获取得到战场情报信息相当于得到获胜的钥匙,为了获取更全面的战场信息,慢速、低空飞行的旋翼类飞行器无疑是最好的选择[1],旋翼类飞行器主要包含有直升机,螺旋桨飞机,以及近几年比较火的无人机。基于脉冲多普勒雷达平台,因为窄带雷达的局限性,仅仅能获取目标的一些例如速度、距离等运动信息[2-5]。但仅仅依靠这些信息,似乎有些单薄;现在的方向,已经不仅仅是对目标测距和测速,越来越向智能化雷达发展。本文探索奇偶旋翼对雷达时域回波的影响,对旋翼类目标的目标识别提供了新的思路[8]。
本文基于窄带雷达时域回波,构建了旋翼叶片回波的散射点模型,利用物理分析阐述了桨叶反射现象出现的原因;同时也分析了奇旋翼和偶旋翼类旋翼机产生的雷达回波的差异,并根据实测数据进行分析论证。
1 飞机旋翼雷达回波建模分析
1.1 桨叶模型
考虑到雷达照射旋翼类目标都是仰视,在旋翼转动中,不考虑机身对旋翼的遮挡情况下,可以用图1来模拟旋翼绕旋转轴转动的模型,此处可以将旋翼看做为L×H的矩形反射面。
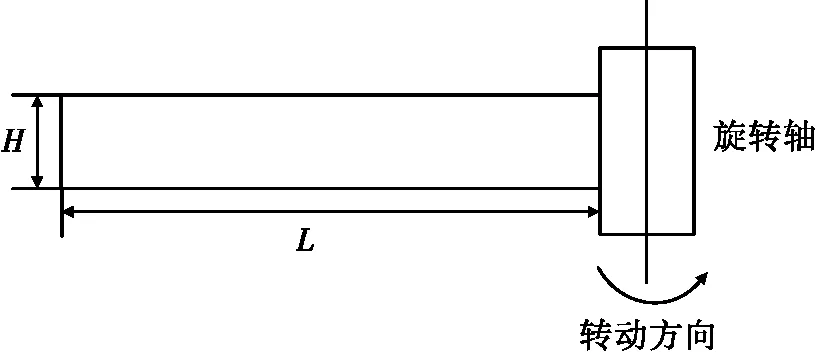
图1 桨叶转动模型
图1所示为桨叶转动模型,各式各样的旋翼机的桨叶旋翼都有所差别,用来模拟各种错综复杂的桨叶旋翼的运动状态,利用L×H的矩形反射面来描述足以说明其物理依据。L×H的矩形反射面的雷达反射截面积σLH可以表示为
(1)
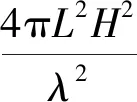
(2)
当x=0时取最大值,在x=±π时会取到第二大峰值。可以得到雷达反射截面积(RCS)σLH会随着θ变化的示意图如图2所示。
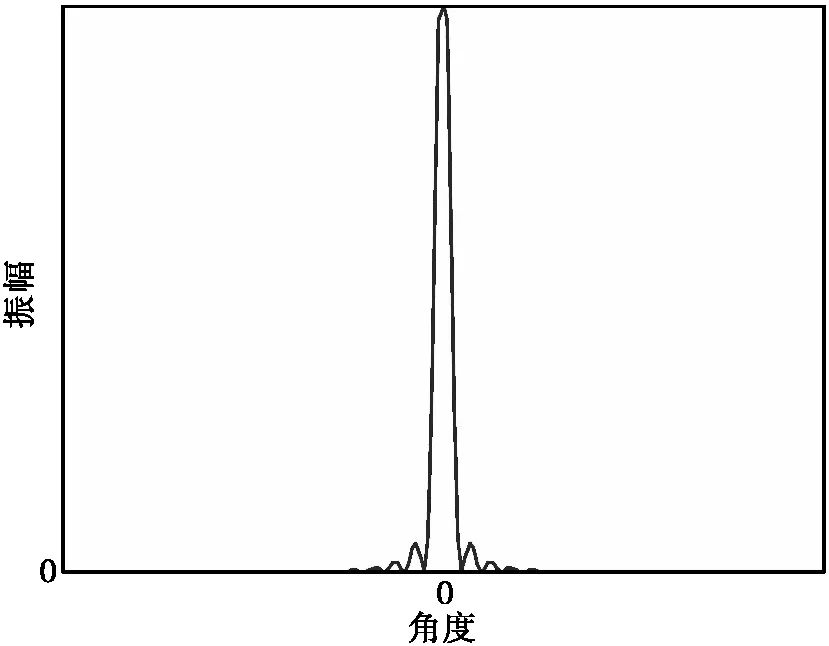
图2 雷达反射截面积随入射角度变化示意图
图2为L×H的矩形反射面的雷达反射截面积(RCS)仿真图,可以看出,该曲线关于入射角度呈偶函数分布,可以考虑用幅度为0的两个波谷之间的距离来表示峰值宽度,当θ满足(2π/λ)Lsinθ=±π时,可以得到最大的雷达反射截面积(RCS),此时满足:
(3)
其中,λ≪L⟹λ/L≈0,以及sinθ关于θ是一阶无穷小量,峰值宽度w可以表示为
(4)
从图2可以看出,为了能观测到桨叶回波的峰值,必须保证雷达照射信号垂直于旋翼的桨叶,根据辛格函数的特性,当入射角度稍有偏差,回波信号将大幅下降。也就是说,只有当入射角度垂直时才能接收到强的信号,而其他角度接收到的都是低强度的回波,这个现象被称为“桨叶反射”[7]。
1.2 奇偶桨叶反射信号分析
旋翼桨叶的数量也可以影响桨叶反射信号的探测。图3给出了四旋翼桨叶与雷达位置示意图。
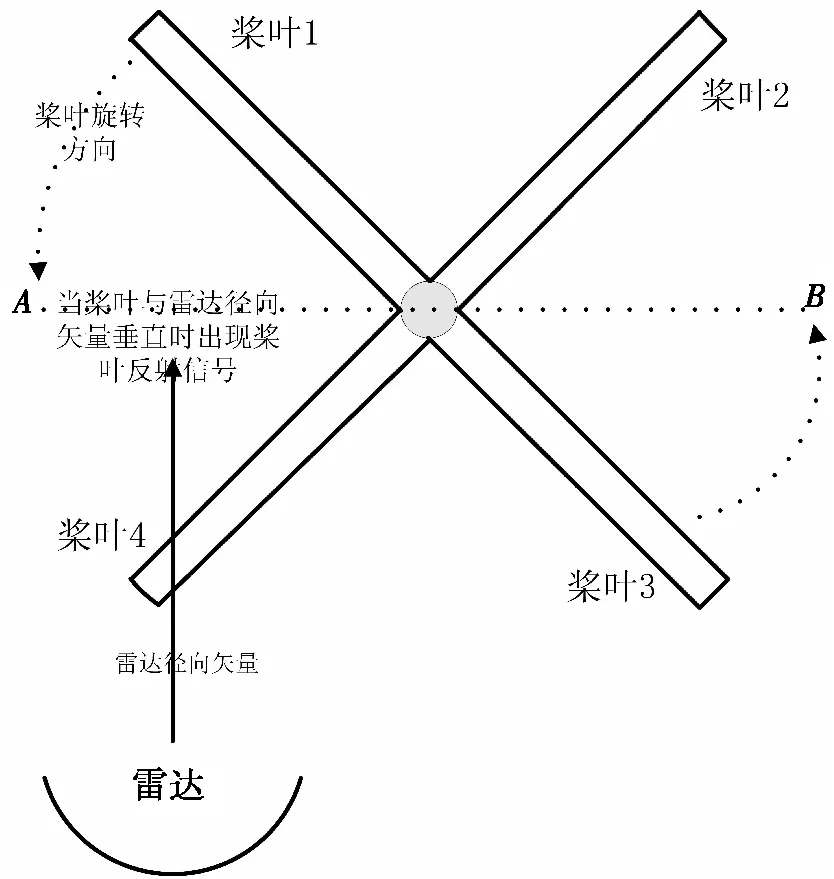
图3 四旋翼桨叶与雷达位置示意图
图3所示为四旋翼桨叶转动模型,对于四旋翼的桨叶,当其任意一片桨叶垂直于雷达的波束指向时,就会发生相应的桨叶反射。不妨设AB所在的直线为与雷达径向矢量垂直的位置,当桨叶1转到位置A时,同时桨叶3会转到位置B,在雷达照射方向不变的情况下,桨叶1和桨叶3几乎都会产生桨叶反射,而反应在回波上,则是桨叶1和桨叶3的回波之和。所以在一个转动周期内,一个四桨叶的旋翼可以探测到四次桨叶反射。可以推广到所有偶数个桨叶中,即旋翼桨叶以R0Hz的频率转动,则具有偶数桨叶的桨叶反射信号出现的频率Bf可以表示为
Bf=NR0
(5)
式(5)中:Bf为桨叶反射信号出现的频率,其单位为Hz;N是旋翼桨叶的数量。
在旋翼转动时,偶数桨叶每次出现桨叶反射现象的位置都高度对称,即当桨叶1到A位置时,桨叶3到B位置,而时域回波上,则是桨叶1在A位置与桨叶3在B位置上桨叶发射信号的叠加。同时,如果以式(5)的频率对雷达回波进行观测,可以得到完整的桨叶反射,经过傅里叶变换积累得到的频率谱也较为完整。
对于奇数片叶片时,桨叶反射可能会有所不同。以三旋翼桨叶为例,其桨叶与雷达位置示意图如图4所示。
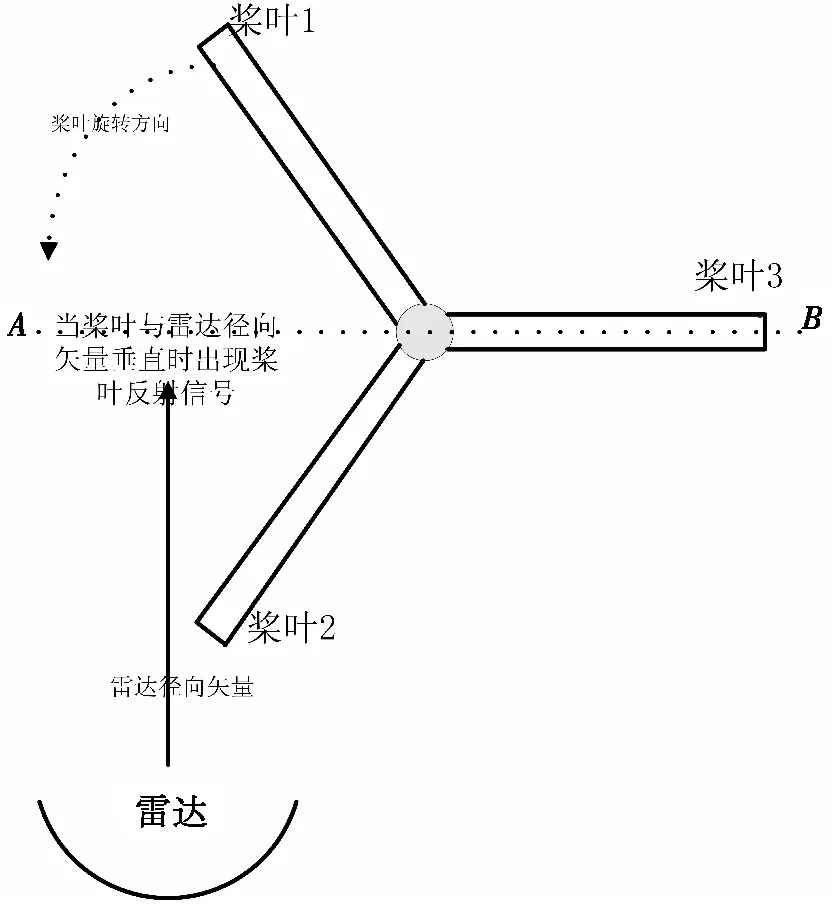
图4 三旋翼桨叶与雷达位置示意图
图4所示为三旋翼桨叶转动模型,不妨设AB所在的直线为与雷达径向矢量垂直的位置,假设当桨叶3处于垂直雷达径向矢量的位置,会出现相应的桨叶反射信号,与偶数叶片的旋翼不同的是,当桨叶3出现桨叶反射信号时,其他桨叶不会出现桨叶反射信号。也就是说,在旋翼旋转一周的情况下,每个桨叶会分布出现在位置A和位置B各一次,且不会出现两个桨叶同时发生桨叶反射的情况,即每个桨叶叶片会单独出现两次桨叶反射。所以与具有偶数片桨叶的旋翼相比,奇数叶片的旋翼产生桨叶反射的频率会增大一倍。
当旋翼个数为奇数时,不妨设旋翼桨叶以R0Hz的频率转动,那么出现桨叶反射信号的频率Bf可以表示为
Bf=2NR0
(6)
式(6)中,Bf为桨叶反射信号出现的频率,其单位为Hz,N是旋翼桨叶的数量。
在奇数旋翼转动时,每片桨叶会产生两次桨叶反射信号,且一般出现在对称位置,由于雷达照射旋翼机一般都是仰视,因为机身遮挡等原因,每片桨叶的两次桨叶反射信号回波强度有较大差异,即在奇数旋翼旋转1周的时间内,会出现NR0次强桨叶反射回波和NR0弱桨叶反射回波。
2 实测数据分析与论证
对于奇偶旋翼的回波特性,本文分别以四旋翼和五旋翼飞行器进行仿真验证。若根据飞行器的飞行参数和桨叶个数计算得到出现桨叶反射的频率与根据雷达回波计算得到是桨叶反射的频率相当,则可以判断上述分析正确。
已知五旋翼飞行器旋翼转速为192r/min,四旋翼飞行器旋翼转速为350r/min,某雷达脉冲重复频率为10kHz,对四旋翼和五旋翼飞行器的雷达回波进行分析处理。
四旋翼雷达回波如图5所示。
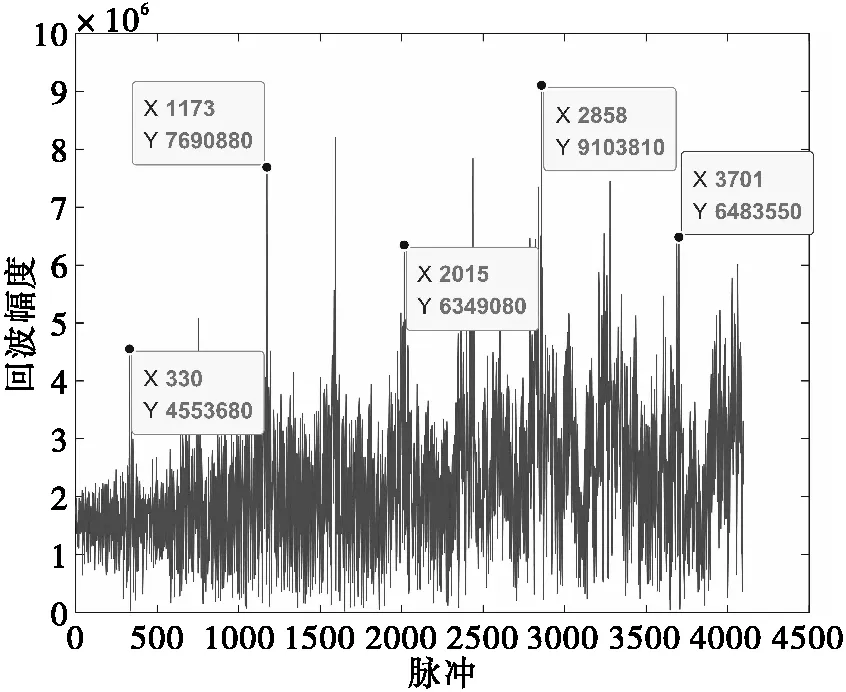
图5 四旋翼飞行器回波幅度图
由图5可以看出,相邻波峰,即出现桨叶反射的间距为421个脉冲,折合时间间隔为42.1ms,而根据四旋翼飞行器的参数,桨叶转速为350r/min,则其旋翼转动周期为0.1714s,则每个旋翼出现桨叶反射的周期为42.9ms。即实测数据的桨叶反射间隔为42.1ms,理论上桨叶反射间隔为42.9ms,误差为1.9%,在接受范围内。综上所述,实测值与理论值一致,说明图5所述峰包确为四旋翼桨叶的桨叶反射所引起的。
五旋翼雷达回波如图6所示。
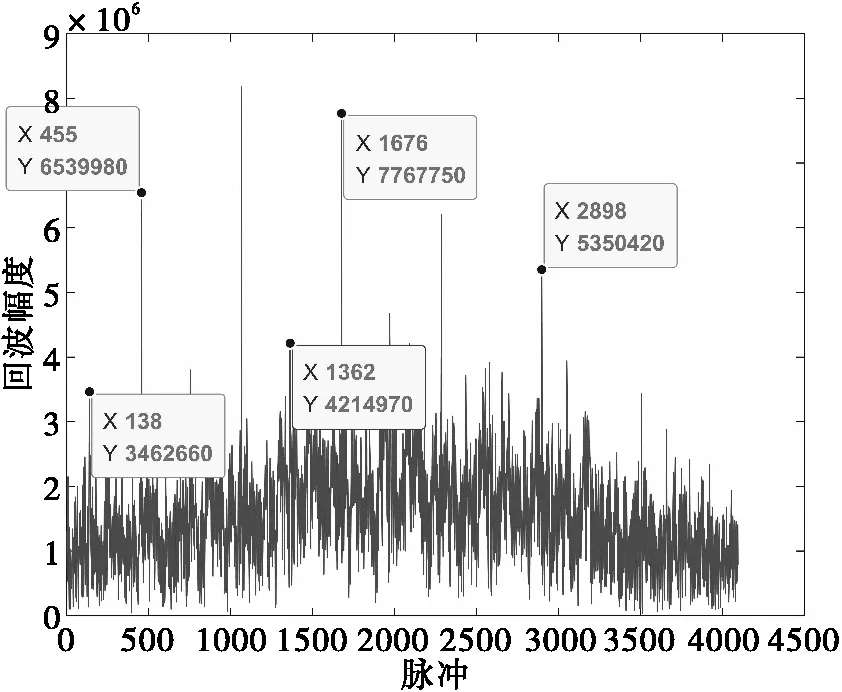
图6 五旋翼飞行器回波幅度图
由图6可以看出,五旋翼为奇数旋翼,出现一强一弱相交错的桨叶反射。脉冲重复频率为10kHz,强桨叶反射的间距为611个脉冲,折合时间间隔为61.1ms;弱桨叶反射的间距为612个脉冲,折合时间间隔为61.2ms。可以得出,实测数据与理论推导吻合,一强一弱相交错的桨叶反射间隔一致,弱脉冲为桨叶反射被机身遮挡一部分所产生。而根据五旋翼飞行器的参数,桨叶转速为192r/min,则其旋翼转动周期为0.0625s,则每个旋翼出现桨叶反射的周期为62.5ms。而实测数据的桨叶反射间隔为61.2ms,理论上桨叶反射间隔为62.5ms,误差为2.08%,在接受范围内。综上所述,实测值与理论值一致,说明图6所述峰包确为五旋翼桨叶的桨叶反射所引起的,同时也验证了奇数桨叶会出现NR0次强桨叶反射回波和NR0弱桨叶反射回波。
3 结束语
本文探究了奇偶旋翼对雷达回波的影响。根据桨叶反射现象的物理特征,分析了奇偶旋翼的飞行器产生桨叶反射现象的差异以及对雷达回波的影响,即偶数旋翼出现桨叶反射次数为NR0次,其中R0为桨叶转动频率,N是旋翼桨叶的数量;偶数旋翼出现桨叶反射次数为2NR0次,但其中会出现NR0次强桨叶反射回波和NR0弱桨叶反射回波,后又根据实测数据验证了该分析的正确性。本文提出的方法能够有效地验证奇偶旋翼对雷达时域回波的影响,为旋翼类飞行器的目标识别提供了新的思路。

