一道课本习题的解答引起的联想
甘肃临泽一中 (邮编:734200)
问题1 (人教版.普通高中课程标准实验教科书.数学2.必修A版,第132页习题4.2A组第11题)
求经过点M(3,-1)且与圆C:x2+y2+2x-6y+5=0相切于点N(1,2)的圆的方程.
常规解法设所求圆的方程为(x-a)2+(y-b)2=r2.
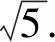
由题意,可得
(1)
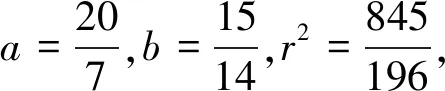
故所求圆的方程为
关于a、b、c的方程组(1)容易列出,但解该方程组运算量非常大,既要平方去根号,又要代入消元,这对学生数据处理能力的考查要求非常高,绝大多数学生会因为运算量太大而半途而废,怎么办?有无简便方法?
联想1 若圆C1:x2+y2+D1x+E1y+F1=0 ,圆C2:x2+y2+D2x+E2y+F2=0,则过两圆交点的圆方程可设为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0.
题目中已知的圆只有一个,怎样再找一个呢?
联想2 若圆的一条直径的两端点分别是A(x1,y1),B(x2,y2).
则此圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0.
题目中只有一个切点,并不是两个交点,怎么办?
联想3 利用极端化思想
若把直线与圆相切视为直线与圆相交的特殊情形,把切点视为重合的两交点,则可设过切点N(1,2)的圆方程为(x-1)(x-1)+(y-2)(y-2)=0,即点圆(x-1)2+(y-2)2=0.
于是可得下面的简便解法:
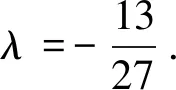
结论1 若圆C与圆C1:x2+y2+D1x+E1y+F1=0切于点P(x0,y0),则圆C的方程可设为(x-x0)2+(y-y0)2+λ(x2+y2+Dx+Ey+F)=0.(易证,略)
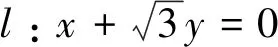
常规解法设圆C的方程:(x-a)2+(y-b)2=r2.又圆C1的圆心C1(1,0),半径为1,

(2)
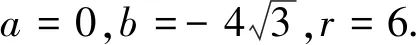
同样,关于a、b、r的方程组(2)容易列出,但解该方程组运算量非常大,既要平方,又要去绝对值符号,怎样才能简少运算量,迅捷解决问题呢?
联想4 若直线l:Ax+By+C=0 ,圆C1:x2+y2+D1x+E1y+F1=0,则过直线l与圆C1交点的圆方程可设为x2+y2+D1x+E1y+F1+λ(Ax+By+C)=0.
题中已知的圆只有一个,利用切点再找一个.
联想5 利用极端化思想
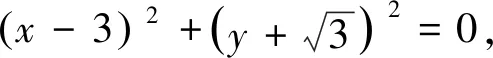
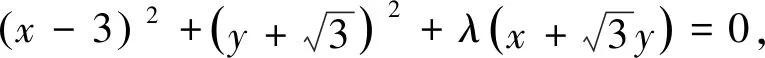
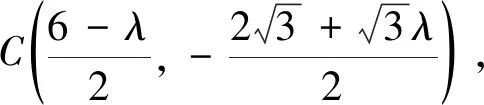
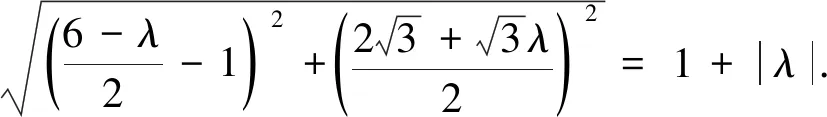
化简得λ+6=2|λ|,
从而得λ=6或λ=-2.
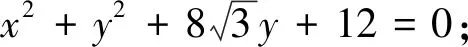
当λ=-2时,圆C的方程为x2+y2-8x+12=0.
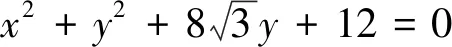
结论2 若圆C与直线l:Ax+By+C=0切于点P(x0,y0),
则圆C的方程可设为(x-x0)2+(y-y0)2+λ(Ax+By+C)=0.(很容易证明,本文略)
由此可见,在求圆方程时,对于有关切点的问题,若能利用极端化思想,大胆联想,积极探索,定可事半功倍,巧妙解决问题.
巩固练习
2.已知圆C与圆C1:x2+y2-2y=0相外切,并且与直线l:x+y-7=0相切于点N(4,3).求圆C的方程(答案:x2+y2-4x-2y+4=0).

