变换 数学解题中一道亮丽的风景
2019-04-18 03:39湖北省武汉市黄陂区第一中学盘龙校区邮编430312
中学数学教学 2019年2期
湖北省武汉市黄陂区第一中学盘龙校区 (邮编:430312)
湖北省武汉市黄陂区第一中学 胡 萍 (邮编:430300)
法国科学家贝尔纳曾指出:良好的方法使我们更好地发挥运用天赋的才能,而拙劣的方法会抑制才能的发挥,可见解决问题时选择一种好的方法至关重要,这既能使我们高效快捷地达到目的,又有利于我们提升能力.本文结合实例谈谈数学变换在优化解题中的巧妙应用.
1 平移
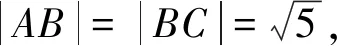
解由y=x3-6x2+13x-9得y=(x-2)3+(x-2)+1,它的图象可由奇函数y=x3+x的图象向右平移两个单位,向上平移一个单位得到,先来考虑问题的简单情形:
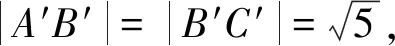
点评例1中的函数图象都是中心对称图形,经过平移将对称中心移至坐标原点,简化了问题,优化了解题过程,体现了转化的思想.
2 对称
例2 (武汉市2019届高三二月调考第12题简编)f(x)=ex-aln(ax-a)+a(a>0),关于x的不等式f(x)>0恒成立,则实数a的取值范围为______.
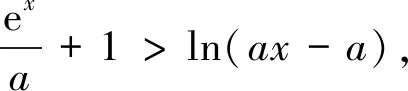
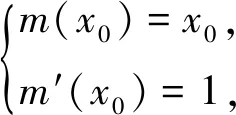
点评将问题归结为两个我们较为熟悉的函数图象间的位置关系解决,观察出m(x)与n(x)的图象关于直线y=x对称,将问题化归为其中一个函数图象与直线y=x的图象位置关系是关键,考验学生的直觉思维.
3 伸缩
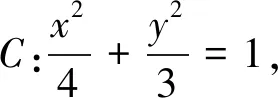
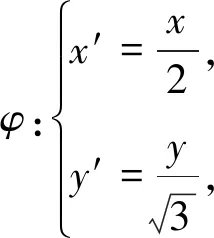
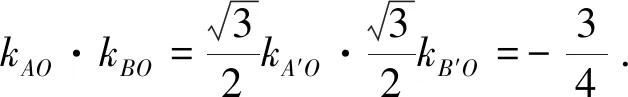
点评利用伸缩变换将椭圆还原成圆,增强了图形的“几何特征”,为借用平面几何方法解决问题创造了有利条件.
4 旋转
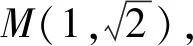
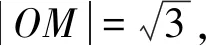
当且仅当4k2+1=k2+4,即k=±1;
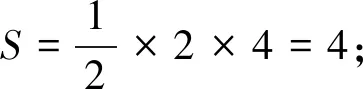
综上四边形ABCD面积的最大值为5.
点评抓住四边形的面积仅与点M同圆心的距离有关这一本质,借助旋转,将点M移至坐标轴上,简化了直线方程的形式,减少了计算.
从以上几例不难发现,无论是平移、伸缩还是旋转,本质上都是将复杂的问题简单化,体现了数学中转化的思想,对图形进行合理变换能降低计算难度,明晰解题方向,优化解题过程,是一种很好的解题策略.
猜你喜欢
音乐天地(音乐创作版)(2020年12期)2020-12-06
民族大家庭(2020年6期)2020-11-29
新世纪智能(教师)(2019年1期)2019-09-11
人物画报(2019年2期)2019-09-10
中国生殖健康(2019年2期)2019-08-23
数学大王·低年级(2018年2期)2018-02-02
绿色科技(2017年18期)2017-11-01
绿色科技(2017年13期)2017-07-31
中华建设(2017年2期)2017-06-01
中国中西医结合影像学杂志(2013年5期)2013-08-15

