探究让考题更精彩*——一道学考题的探究与思考

●

(乐从中学，广东 佛山 528315)

1 原题呈现与解答

例1已知抛物线C:y2=4x的焦点是F，准线是l.

1)写出点F的坐标和准线l的方程；

图1

2)如图1，已知点P(9,6)，若过点F的直线交抛物线C于两个不同的点A,B(均不与点P重合)，直线PA,PB分别交l于点M,N，求证：MF⊥NF.

(2018年11月浙江省数学学考试题第23题)

本题是以直线和抛物线相交为背景的试题，主要考查直线与抛物线的位置关系、直线的斜率及直线方程、抛物线等基础知识和运算求解的基本技能，突出考查学生的数量转化、运算与推理论证等能力.具有一定的开放性和探索性，较好地体现了新课改理念，对考生的数学思维水平和数学素养有较高的要求.

分析1)由题意得点F的坐标为(1,0),直线l的方程为x=-1.

2)设A(x1,y1)，B(x2,y2)(其中y1≠±6,y2≠±6),设直线AB的方程为x=ty+1[1].联立

得

y2-4ty-4=0，

从而

y1+y2=4t,y1y2=-4.

由P(9,6)，得

从而直线PA的方程为

将y1+y2=4t,y1y2=-4代入，化简得

kFMkFN=-1,

故

MF⊥NF.

2 借题发挥，结论推广

数学家波利亚曾说：“解题就像采蘑菇一样，当我们发现一个蘑菇时，它的周围可能有一个蘑菇圈.”解答完本题后，思考：这个结论能否在抛物线中一般化，解答方法是否依然有效？经进一步探究，可得如下结论：

结论1已知抛物线C:y2=2px(其中p>0)的焦点是F，准线是l.若点P在抛物线上，过点F的直线交抛物线C于不同的两个点A,B(均不与点P重合)，直线PA,PB分别交l于点M,N，则MF⊥NF.

得

y2-2pty-p2=0，

于是

y1+y2=2pt,y1y2=-p2.

于是直线PA的方程为

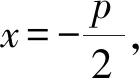
将y1+y2=2pt,y1y2=-p2代入，化简得

kFMkFN=-1,

故

MF⊥NF.

3 更进一步，寻求简洁证法

从上述证明可以看出,用解析法虽然可以证得结论，但运算量较大，那么有没有更为简单的方法呢？经探索，找到了一个极为简洁的证法.

由于结论1的证法2及后面相关结论的证明都要用到一些定理，这里先行给出以下两个定理与3个引理：

图2 图3

引理1若抛物线的焦点为F，抛物线的弦AB延长后交准线l于点K，则FK平分FA与FB夹角的外角.

证明如图4,分别作AM⊥l于点M,BN⊥l于点N.易得△AKM∽△BKN，即

由抛物线的定义，知

AM=AF,BN=BF，

从而

由定理2可得FK平分∠BFG，即FK平分FA与FB夹角的外角.

图4 图5

引理2若椭圆的焦点为F，椭圆的弦AB延长后交对应的准线l于点K，则FK平分FA与FB夹角的外角.

证明如图5,分别作AM⊥l于点M,BN⊥l于点N.易得△AKM∽△BKN，从而

由椭圆的第二定义，知

于是

故

由定理2可得FK平分∠BFG，即FK平分FA与FB夹角的外角.

引理3若双曲线的焦点为F，双曲线的弦AB(或延长后)交对应的准线l于点K.

1)如果点A,B在双曲线的同一分支上，则FK平分FA与FB夹角的外角；

2)如果点A,B在双曲线的不同一分支上，则FK平分FA与FB夹角.

引理3中1)的证明与引理2的证明一样；引理3中2)的证明要用到定理1(三角形内角平分线定理的逆定理)，证明过程与引理2的证明类似，在此略去.

图6

结论1的第二种证法如下：

证法2如图6，联结PF，并延长交l于点G.由引理1可得FM平分∠AFG，FN平分∠BFG，且∠AFG+∠BFG=180°，从而

2(∠MFG+∠NFG)=180°，

即

∠MFG+∠NFG=90°，

于是

∠MFN=90°，

故

MF⊥NF.

本证法借助三角形外角平分线定理的逆定理、抛物线的定义以及抛物线中弦与准线的相关引理，从平面几何的角度思考，简化了推理和运算过程，具有直观、简捷、明快的特点，方法新颖独到.

4 探究延伸，类比性质

我们知道，圆锥曲线一般有着类似的性质，这体现了圆锥曲线性质的内在统一的和谐美.那么椭圆与双曲线中是不是也具有类似结论1的性质呢[2]？经探究，发现如下两个结论：

结论2已知椭圆C的焦点是F，对应的准线是l.若点P在椭圆上，过点F的直线交椭圆C于两个不同的点A,B(均不与点P重合)，直线PA,PB分别交l于点M,N，则MF⊥NF.

结论3已知双曲线C的焦点是F，对应的准线是l.若点P在双曲线上，过点F的直线交双曲线C于两个不同的点A,B(均不与点P重合)，直线PA,PB分别交l于点M,N，则MF⊥NF.

结论2与结论3的证明可参照结论1的证法2，限于篇幅，在此不再给出，留给感兴趣的读者.

5 探究后的启示

解析几何是用代数方法解决几何问题，在教学中我们往往注重解析几何的代数运算，轻视其几何推理.其实解析几何问题本质是几何问题，它们本身就包含一些重要的几何性质，若可以充分利用这些几何性质，则可以避开繁琐的代数运算，使解决问题的过程得到简化，解法简洁优美，并更好地揭示这些问题的几何本质.因此对于解析几何问题，要紧扣其中的关键几何要素，将解析法与平面几何方法相结合，从而得到解决问题的最优解法，这不仅是解决解析几何问题的法宝，还是减少解析几何运算量的有效途径，同时可以更好地提高解题能力[3].

对题目的拓展、引申、变式探究是一名数学教师必备的专业素养，平时要重视对典型问题进行深入研究，探索规律，并适当拓展，充分挖掘题目的育人价值.高中数学新课程的理念之一是倡导积极主动、勇于探索的学习方式.在教学中，要引导学生不能只满足于问题的解决，而是要通过变式、类比进行研究，寻求问题的增长点，从而达到“做一题，会一类，甚至会一片”的目的；让学生体验数学的发现和创造历程，引导他们勇于发现问题、提出问题、解决问题，让学生在解题思路上产生质的变化，使思维得到发展，进而全面提高学生的综合能力，提升学生的数学核心素养.