审题 联想 反思*
——智慧学校环境下初中数学习题教学的“三部曲”
●
(上派初级中学,安徽 肥西 231200)
●阮 征
(合肥师范学院数学与统计学院,安徽 合肥 230601)
●韩芬芬 程先寿
(卫德彬初中数学名师工作室,安徽 肥西 231200)
1 问题的提出
习题教学是初中数学课堂教学的一个重要组成部分,也是学生的主要学习活动,更是反映学生数学能力和数学素养的主要途径.通过习题教学,学生能够检测出自己的学习效果,教师可以总结出自己平时教学上的得失,教育主管部门也能了解到不同教师的教学质量优劣.另外,随着近年来的大数据、互联网、云计算等智能化信息技术在数学教学领域的层层深入,出现了一种新型的智慧学校环境[1].所谓智慧学校,即指在数字校园的基础上,建构一个智慧的校园学习环境,这个环境以各种应用服务为载体,能够将教学科研、学校管理和校园生活进行充分的融合[2].在具体的课堂上则表现为每人手中一个平板,教师利用智慧学校平台资源,有目的地向学生端推送素材,师生通过系统对话完成学习内容.本文就将智慧学校环境与初中数学习题教学相结合,在实践的基础上总结教师对于智慧学校环境下习题教学的“三部曲”——“审题、联想、反思”的分析.
2 智慧学校环境下习题教学的“三部曲”分析
2.1 审题是解题的关键
“良好的开端是成功的一半”,审题就是解题前将题目细心阅读,仔细观察结构特征,并认真进行分析和思考.教师在智慧学校环境下指导学生审题的过程中,需要让学生把握好以下4点:
2.1.1 题目类型与常用方法
说到数学题目类型的划分,无非就是选择题、填空题、判断题、解答题和证明题.常用识记法、直接法、特例法及图解法解决选择、填空和判断这3种题型,其中选择题还可以选用筛选法和验证法,而反证法在判断题中还可以派上用场;另外,配方法、换元法、待定系数法和数形结合法无疑是解答题常用的“法宝”;具有压轴性质的证明题常采用分析法和综合法,有时则可利用反证法出奇制胜.而在智慧学校环境下使用每种方法的解题过程均能够展现得活灵活现,由此也深化了学生对解题方法的理解.
2.1.2 已知条件和解题要求
智慧学校平台环境能够清晰地将题干中的已知条件与解题要求用不同的颜色凸显出来,因为明确已知条件与解题要求,不仅能使学生有效利用条件,还能使他们在解题过程中做到心中有数、有的放矢.
2.1.3 题目难易和解题关键
把握题目难易,做题本着先易后难的原则尤为关键.学生通过智慧学校平台环境的提示能够找准突破口、探索解题途径、迅速入门并随之速战速决.
2.1.4 隐含条件与解题策略
对于题目中所隐含的条件,智慧学校平台能够根据已知条件和解题要求,结合题目的结构特征,设法使其明显化,进而扫除学生的解题障碍,使他们能够灵活确定解题策略.
另外,学生审题习惯的培养也不容忽视,首当其冲的是培养学生的读题能力.智慧学校平台的出现能够有效帮助学生读懂题意,并使学生以此为突破口,清除审题障碍、弄清题意,逐渐做到脱离题目也可准确说出已知条件和解题要求等.因此,在智慧学校平台的支持下,学生可以养成良好的审题习惯,从而有效避免了学生平时做题时自我感觉良好(即以为自己一看就会做,结果却是一做便出错)的错误心态.

图1
例1如图1,已知四边形ABCD中,E,F分别是AB,DC边的中点,N是对角线AC的中点.求证:BC+AD≥2EF.
审题本题属于证明题,宜采用分析法,需要求证的是“四边形ABCD的两条对边BC与AD的长度之和”是否大于“四边形另外两条对边AB,DC中点的连线EF的2倍长”.由题干的已知条件“三角形两条边的中点”可以联想到“中位线”这个隐含条件,如果将EN,FN联结起来,就会完整地出现两个三角形的中位线,由此可得
BC=2EN,AD=2FN,
从而
BC+AD=2(EN+FN).
又EN+FN≥EF,于是
BC+AD≥2EF.
通过智慧学校平台的审题分析,使学生明确了已知条件与解题要求,有了正确的思路和方向,找到了题目的隐含条件,进而获得了正确的解题策略.化难为易使问题得到解决,更培养了他们的观察能力.可以说在智慧学校平台环境的支持下,审题作为“三部曲”的“首部”,更是解题的关键,不容忽视.
2.2 联想是解题的翅膀
联想就是对题目所涉及的知识和可能出现的情况加以思索、推测和猜想.通过对审题的深思、联想能够拓宽学生的思路,强化常见的数学思想和方法的应用,沟通知识间的纵横联系,增强学生数学思维的灵活性、严密性、敏捷性、深刻性和创造性,从而培养学生的思维能力.另外,习题教学需要让学生注重联想过程,它分为两个阶段:第一阶段是对被证结论的联想——执果索因,即根据结论特征和要求来进行有目的、有选择地联想;第二阶段是对已知条件及图形的联想——由因导果,即对已知条件所提供的各种信息进行相应的有关定理、概念等知识的联想,也就是先研究对特征结论联想的结果,然后对已知条件并结合图形进行联想,最后将相关的知识点用分析推理的方式连接起来,从中得出最佳证明方案.而智慧学校平台环境则恰到好处地辅助了学生对于题目的联想,下面结合一道几何证明题进行说明:
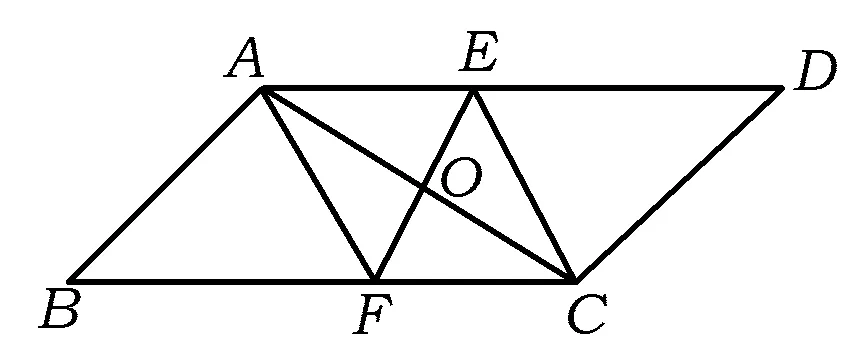
图2
例2如图2,ABCD的对角线AC的垂直平分线与边AD,BC分别相交于点E,F,求证:四边形AFCE是菱形.
1)对被证结论的联想(第一阶段).
通过智慧学校平台环境提供的提示素材可知,由“四边形是菱形”这个被证结论可以联想到菱形的判定定理:①四边都相等的四边形是菱形;②对角线互相垂直的平行四边形是菱形;③一组邻边相等的平行四边形是菱形;④对角线互相垂直平分的四边形是菱形……学生结合图2有了下面的联想:
四边形AFCE是菱形⟹

紧接着,智慧学校平台对“由被证结论的联想得到的判定条件”一一进行再次联想的提示:图2需要满足怎样的条件才能符合先前判定“四边形AFCE是菱形”的条件?于是学生便有了如下的联想:


2)对已知条件及图形的联想(第二阶段).
智慧学校平台也对已知条件及图形的联想提供了提示素材:从四边形是平行四边形以及对角线的垂直平分线能够联想到哪些条件?学生联想到平行四边形和垂直平分线分别具有的性质,具体进行了以下联想:
四边形ABCD是平行四边形⟹
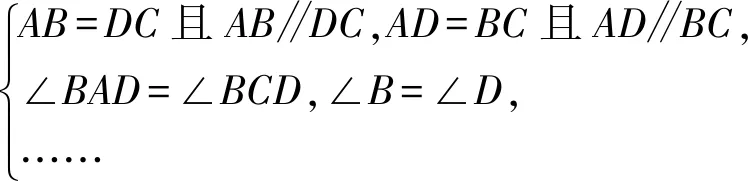
EF是AC的垂直平分线⟹
3)处理联想结果,确定证明方案.
由于要进行全面联想和系统研究,得出的证明方案往往不止一个,借助智慧学校平台的引导,学生进行综合比较分析,最终得到了以下最佳证明:
证明因为四边形ABCD是平行四边形,所以
AD∥BC,
从而
∠EAO=∠FCO.
又因为EF是AC的垂直平分线,所以OA=OC.
在△AOE和△COF中,
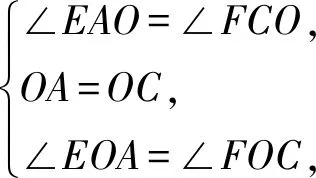
从而
△AOE≌△COF(ASA),
于是
OE=OF.
由OA=OC知四边形AFCE是平行四边形,又EF是AC的垂直平分线,故AFCE是菱形.
分析本题难度适中,主要考查了平行四边形的性质和判定、菱形的判定、全等三角形的性质和判定、线段垂直平分线性质的应用,而这些也是引发学生两个阶段联想的载体,证明此题的关键是证明三角形全等.可以发现,通过智慧学校环境的辅助,不仅能够拓宽学生的思路,还能提高他们灵活运用知识的能力.学生为了能够充分的联想,将调动大脑中的所有相关信息,并予以加工,这也考查了学生思维的广阔性和参与实践的主动性,使每个学生都能有所收获.可以说在智慧学校环境的帮助下,联想作为解题“三部曲”的“中间一部”,就像一双“隐形的翅膀”助力着学生的解题思路.
2.3 反思是解题的深化
反思就是回顾解题得失、回忆如何审题与联想、思考用到哪些知识点、各知识点间有何联系、解题有何技巧、解法有何捷径、解题有无规律等.实践证明,教师给学生提供充分反思解题过程的机会,多关注学生的反思行为,通过多种途径培养学生反思的习惯,不但可以培养学生的自主学习数学的能力,而且还可以激发学生产生勇于探索难题的意识,对学生来说终身受益.因为在数学习题教学中,解(证)完一道题后,并非大功告成,而是需要学生再思考,以求从演练中获得多方面的启示,巩固和扩大演练成果.智慧学校平台环境在这里能够有效地将相关或相近知识串联起来,使学生“做一题,会一串”,从而真正实现举一反三、触类旁通.
通过先前智慧学校环境下的审题和联想解题训练,紧接着进行反思,不仅能巩固所学知识、积累解题经验、总结解题规律、提高解题能力,还可发现一题多解、拓宽思路、选择捷径,甚至还能发现特殊解法,培养学生的特殊思维能力.
例3当(a+b)2=6,(a-b)2=4时,求a2+b2及ab的值.
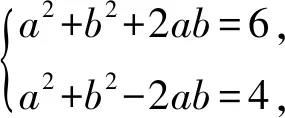
反思通过智慧学校平台的展示反思可知,本题利用了整体思想方法,活用乘法公式,巧用方程组解题.其解法灵活巧妙,过程简洁明快,效果更是事半功倍,使学生的数学思维得到了深化,培养了学生活学活用、举一反三、综合运用数学知识的能力[3].可以说在智慧学校平台的推动下,反思作为“三部曲”的“最后一部”,是解题的深化,更是完美的收官.
3 “审题、联想、反思”解题的训练功能举例
例4若相交两圆的公共弦长为24,两圆半径分别为15和20,求圆心距.
审题已知两圆半径(15和20)及公共弦长(24),要求出的是圆心距.由智慧学校平台推送的素材分析可知,存在两种情况:相交两圆的圆心距可能在公共弦的两旁,也可能在公共弦的同旁.
联想根据智慧学校平台推送的素材,学生可以清晰地联想到:要想求出相交两圆的圆心距,必然用到相交两圆的连心线垂直平分公共弦,以及勾股定理.具体解答如下:
解1)当相交两圆的圆心在公共弦两旁时(如图3所示),
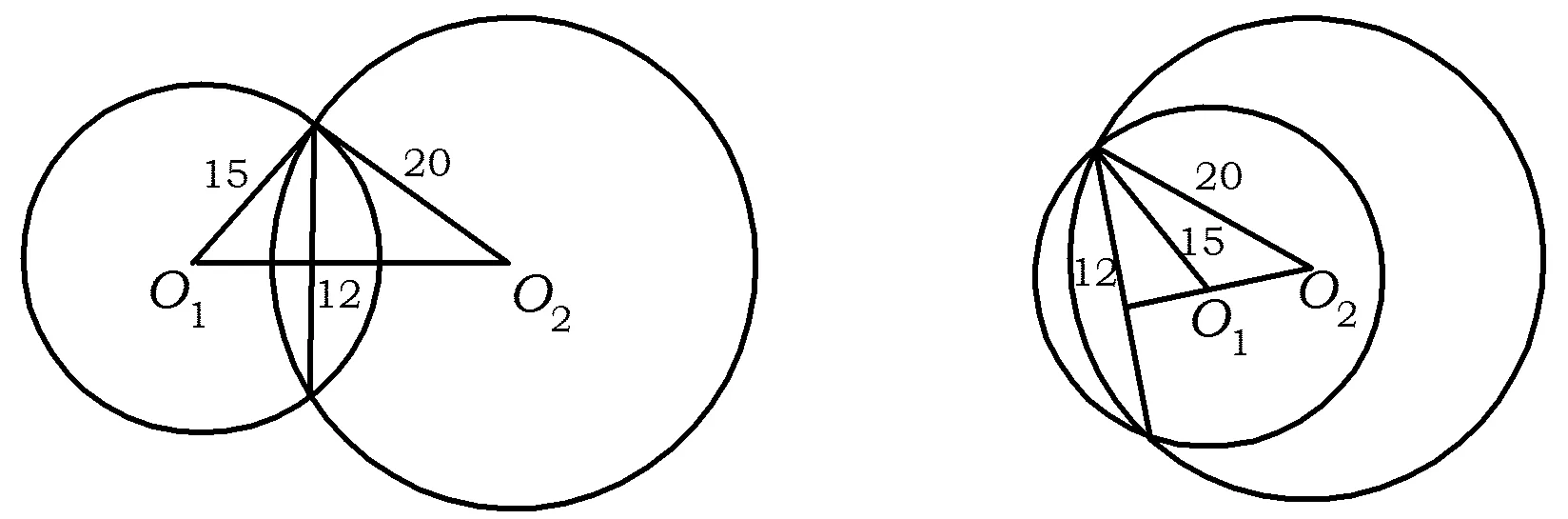
图3 图4
2)当相交两圆的圆心在公共弦同旁时(如图4所示),
反思本题运用分类思想方法,求出所有符合条件的圆心距,通过智慧学校平台的有效提示与归纳,培养了学生思维的严谨性.学生理解了本题后,在脑海中会留下烙印:一般地,相交两圆的圆心距
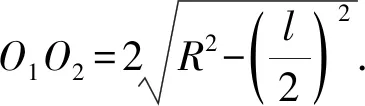
其中R,r表示圆半径,m表示大的弦长,n表示小的弦长.
4 小结
综上所述,智慧学校环境下面向全体学生进行“审题、联想、反思”的初中数学习题教学,一方面能使学生轻松自如的解题,另一方面能使学生所学的知识向纵横、深广和应用等方面发展,优化思维训练.智慧学校平台环境在“三部曲”的各个环节均发挥了不同程度的效用,使“审题、联想、反思”在解题过程中分别扮演着“关键点、翅膀、深化者”的角色,这对于强化学生扎实的数学基本功及非智力因素、提高思维能力和解题能力、推进数学素养大有裨益,更使学生解题后再分析、再思考的习惯得到培养,这样不仅能使学生对知识、技巧深入理解,而且有利于培养学生的探索精神.因此,将智慧学校平台环境与初中数学习题教学相结合是一次成功的尝试,值得大力普及.

