一道抛物线题的一题多解与引申探究

广东省华南师范大学(510631) 陈瑜丹 指导老师: 罗碎海

圆锥曲线是高考必考的重难点内容,主要考察学生的数学思想方法和计算功底.拥有过硬的计算功底是在高考中获得成功的基础,而拥有扎实数学思想方法才能在高考中如虎添翼.下面我们将以一道抛物线题为例作一题多解探究和反思感悟.

一、试题呈现

题目如图1,已知动圆M 过定点F(0,1)且与x 轴相切,点F 关于圆心M 的对称点为F′,动点F′的轨迹为C.

(1) 求曲线C 的方程;

(2) 设A(x0,y0)是曲线C 上的一个定点,过点A 任意作两条倾斜角互补的直线,分别与曲线C 相交于另外两点P、Q.证明: 直线PQ 的斜率为定值.

图1

此题是一道判断直线与圆锥曲线位置关系的综合题,也是经典的“抛物线内接三角形”的问题,题型比较常规,题目分为两小题.第(1)小题主要考察轨迹方程和抛物线的定义,难度较低;第(2)小题主要考察抛物线与直线的位置关系、直线斜率为定值等基础知识,主要考察学生化归转化、设而不求和运算能力等基本技能.

二、试题分析

1、对于第(1)小题: 求曲线C 的方程.

思路一(轨迹法)首先设出点F′的坐标,根据F′和F的坐标表示出圆心M 的坐标, 且|FF′|为圆M 的直径长,由条件“动圆M 与x 轴相切”,可知M 点的纵坐标的绝对值即为圆M 的半径长,从而找出M 点的纵坐标的绝对值与|FF′|的代数关系,即可求解得到点F′的轨迹方程.

解法一设F′(x,y), 由于F(0,1) 在圆M 上, 且点F 关于圆心M 的对称点为F′, 所以圆心M 的坐标为圆M 的直径为又由于圆M 与x 轴相切, 所以即两边平方整理得: x2=4y.所以曲线C 的方程为x2=4y.

思路二(定义法)由已知条件“M 与x 轴相切”以及“点F 关于圆心M 的对称点为F′”可以推出|FF′|为圆M 的直径,M 点的纵坐标的绝对值即为圆M 的半径长,为了找出线段间的数量关系,过点M 和点F′作x 轴的垂线,分别交x 轴于C、D 两点,过点F 作y 轴的垂线,分别交线段F′D和线段MC 于E、N 两点,如图2.得到其中的相似三角形FMN 与FF′E,利用相似三角形的性质以及坐标长度关系就能得出点F′的轨迹满足抛物线的定义,从而得到曲线C的轨迹方程.

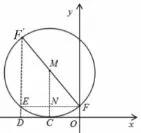
图2

解法二如图2,作MC⊥x 轴于点C,作F′D⊥x 轴于点D,作FE⊥F′D 于点E,则FE⊥MC 于点N,此时△FMN与△FF′E 相似, 相似比为1 : 2, 因此|F′E|=2|MN|,有: |F′F|=2|MF|=2|MC|=2|MN|+2|NC| =2|MN|+2=|F′E|+2=|F′D|+1.因为|F′D| 为点F′到x 轴的距离, 所以|F′D|+1 为点F′到直线y =−1的距离,所以点F′到F 的距离与到直线y =−1 的距离相等.根据抛物线的定义,曲线C 是以F(0,1)为焦点,以直线y =−1 为准线的抛物线,曲线C 的方程为x2=2y.

2、对于第(2)小题: 证明直线PQ 的斜率为定值.

思路一已知条件“过点A 任意作两条倾斜角互补的直线,分别与曲线C 相交于另外两点P、Q”,即直线AP 与直线AQ 的斜率互为相反数,将A,P,Q 三点的坐标分别设出来,即可得到坐标间的关系.但由于涉及到的未知量比较多,因此我们需要利用曲线C 的方程x2=4y 减少未知量的个数,再将P、Q 两点的坐标代入化简即可得到答案.

解法一设P(x1,y1),Q(x2,y2),由于A,P,Q 都在抛物线x2=4y上, 所以由于直线AP 与直线AQ 的倾斜角互补, 所以

图3

kAP+kAQ=0.kAP =所以化简可得: x1+x2=−2x0, 所以kPQ=为定值.

思路二已知条件“过点A 任意作两条倾斜角互补的直线,分别与曲线C 相交于另外两点P、Q”即直线AP 与直线AQ 的斜率互为相反数,分别设出直线AP 与直线AQ 的斜率,结合点A 的坐标分别设出直线AP 与直线AQ 的方程,联立抛物线方程,利用韦达定理就能表示出P、Q 两点的坐标,最后用两点式求出直线PQ 的斜率.

解法二由题意, 直线AP 与AQ 的斜率存在且不为零,设直线AP 的斜率为k,则直线AQ 的斜率为−k.直线AP :y−y0=k(x−x0),联立方程:得: x2−4kx+4kx0−4y0=0,由韦达定理: x0+xP=4k,所以同理: 直线AQ :y−y0=−k(x−x0),联立方程:得: x2+4kx−4kx0−4y0=0,由韦达定理x0+xQ=−4k,所以所以kPQ=为定值.

思路三由条件“过点A任意作两条倾斜角互补的直线,分别与曲线C 相交于另外两点P、Q”, 直接设其中一条直线AP 的倾斜角为θ,从而直线AQ 的倾斜角为π−θ,结合点A 的坐标, 即可设出P,Q 两点的坐标,从而利用两点式求出直线PQ 的斜率,结合P,Q 在抛物线x2=4y 上,对直线PQ 的斜率进行化简.

解法三由于A(x0,y0),设直线AP 的倾斜角为θ,直线AQ 的倾斜角为π−θ,P(x0+|AP|cos θ,y0+|AP|sin θ),

图4

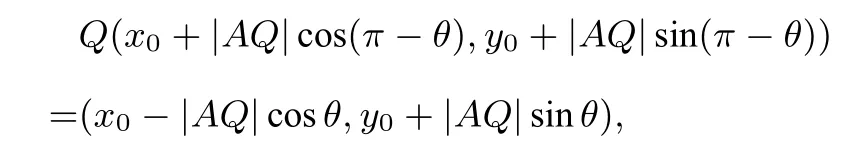
所以

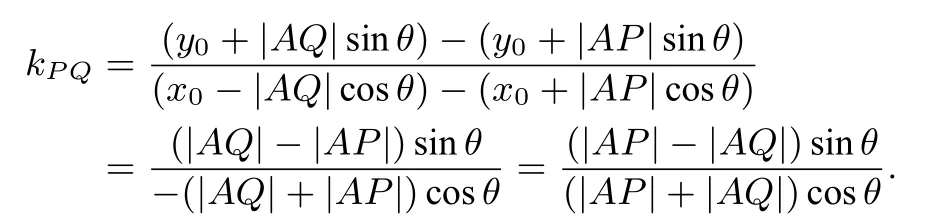
由于P,Q 在抛物线x2=4y 上,所以(x0+|AP|cos θ)2=4(y0+|AP|sin θ),化简可得:

同理: (x0−|AQ|cos θ)2=4(y0+|AQ|sin θ),化简可得:

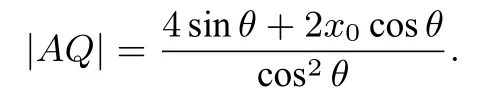
所以

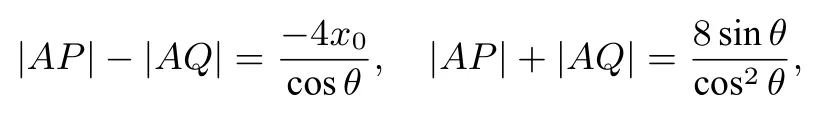
所以

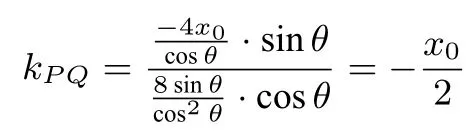
为定值.

思路四不妨先讨论从抛物线顶点O 引出的两条直线与抛物线相交于两点B、C,与顶点构成的三角形OBC 三边之间的斜率的关系,若设B、C 两点的坐标分别为(xB,yB),又为直线BC 与抛物线的交点,为方便解题,设直线BC 的方程为mx+ny =1,与抛物线方程联立,结合韦达定理,可得kOB+kOC=kBC,从而找出A、P、Q 三点与顶点O 相连所成的直线之间的关系,解出直线PQ 的斜率.

解法四过抛物线的顶点O 任意作两条直线,分别于曲线C 相交于另外两点B、C,显然直线OB、OC 和BC 的斜率均存在.设直线BC :mx+ny =1,联立:有:

x2=4y(mx+ny), 整理可得:即: 4nk2+4mk−1=0, 所 以所以由于直线AP 和AQ 是倾斜角互补的两条直线, 因此kAP+kAQ=0, 则0=kAP+kAQ=2kOA+kPQ, 所以kPQ=−2kOA=为定值.

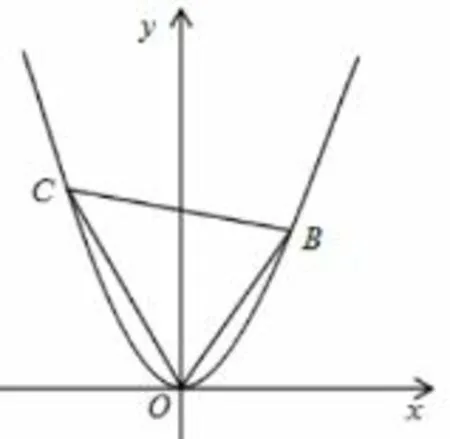
图5

思路五为简化问题, 还可以将坐标原点平移至点A,则抛物线的解析式变为(x+x0)2=4(y +y0), 此时直线AP 和AQ 的斜率可以简化为设直线PQ 为mx+ny=1,与抛物线联立,结合韦达定理即可得到直线PQ 的斜率.

解法五将坐标系原点平移至点A(x0,y0), 则抛物线x2=4y 解析式变为(x+x0)2=4(y+y0), 化简得:x2+2x0x=4y.设直线PQ 为: mx+ny =1,由于直线PQ不可能垂直于x 轴,因此n0.则x2+2x0x·(mx+ny)=4y·(mx+ny),整理得:2mx0)=0, 即: 4nk2+(4m−2nx0)k−(1+2mx0)=0,由于直线AP 和AQ 是倾斜角互补的两条直线, 因此kAP+kAQ=0, 所以为定值.

三、试题探究

波利亚将解决问题的过程分成了四个阶段: 弄清问题、拟定计划、实现计划、回顾,强调在解决完数学问题之后的回顾与反思.养成问题回顾的习惯能够更好地巩固知识,并认清问题的本质.

重新回顾第(2)小问,似乎直线PQ 的某些特点是由直线AP 和AQ 决定的,如果改变直线AP 和AQ 的斜率关系,那么直线PQ 的性质将会如何改变呢? 沿着这个问题作三个简单的探究.原题中的多种解法都可用于探究中,但常规解法更能反映知识的发展、演变过程,为了使得常规解法能够得到充分的理解和掌握,在探究中用到的解法均与解法一类似.

探究一如图6, 设A(x0,y0)为抛物线y2=2px(p > 0)上一定点, 过点A 任意作直线, 分别与抛物线交于另外两点P、Q,α1和α2分别为直线AP、AQ 的倾斜角,若时,直线PQ的有什么特点?

解不妨设tan θ=t, 设P(x1,y1), Q(x2,y2), 由于A,P,Q 都在抛物线y2=2px 上,所以

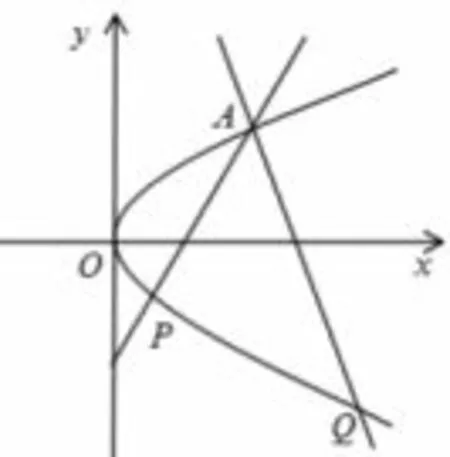
图6

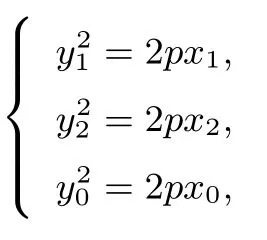
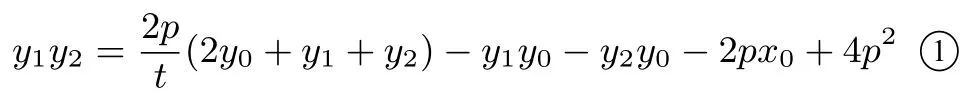
(I) 若kPQ存在, 则直线化简可得:

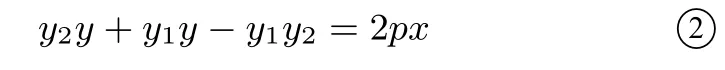
将 ①式中的y1y2代入到 ②式中并整理可得: 直线PQ:因此PQ 过定点

(II) 若kPQ不存在,则P(x1,y1),Q(x1,−y1),将

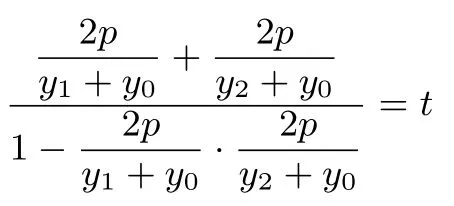
探究二设A(x0,y0)为抛物线y2=2px(p > 0)上一定点,过点A 任意作直线,分别与抛物线交于另外两点P、Q,若kAP+kAQ=t 时,直线PQ 有什么特点?

解设P(x1,y1), Q(x2,y2), 由于A,P,Q 都在抛物线 y2=2px 上,所以

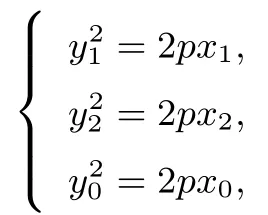
由于kAP+kAQ=t,

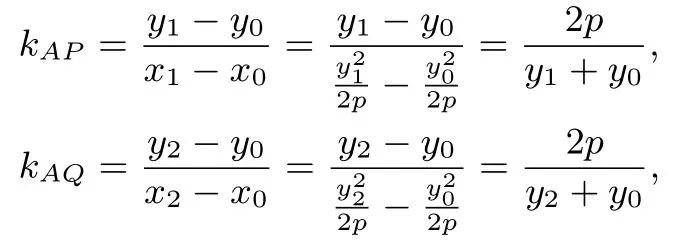
(I) 若kPQ存在,则

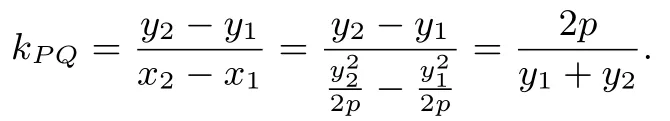
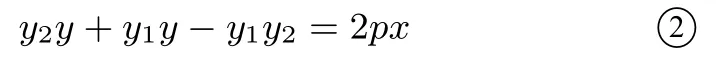
将 ①式中的y1y2代入到 ②式中并整理可得: 直线

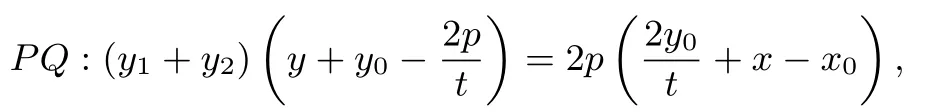
(II) 若kPQ不存在, 则P(x1,y1), Q(x1,−y1) kAP=

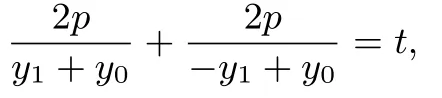
(2) 当t=0 时,有

化简可得: y1+y2=−2y0, 此时, 直线PQ 的斜率必存在.由(1)可知,直线PQ:y2y+y1y−y1y2=2px,将y1+y2=−2y0代入直线PQ 的解析式, 即:−2y0y−y1y2=2px 若y0=0,则直线PQ 与x 轴垂直;若y00,则直线PQ 的斜率为

探究三设A(x0,y0)为抛物线y2=2px(p > 0)上一定点,过点A 任意作直线,分别与抛物线交于另外两点P、Q,若kAP·kAQ =t(t0)时,直线PQ 有什么特点?

解设P(x1,y1), Q(x2,y2), 由于A,P,Q 都在抛物线y2=2px 上, 所以由 于kAP· kAQ=t(t0),

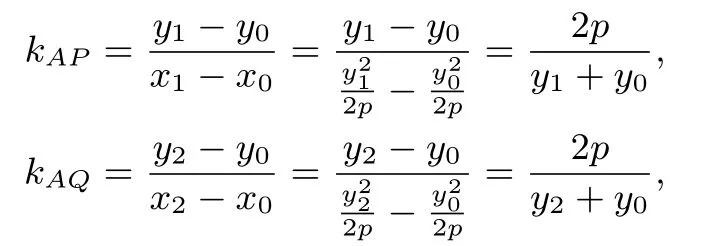
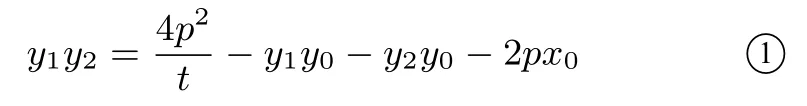
(I) 若kPQ存在,则

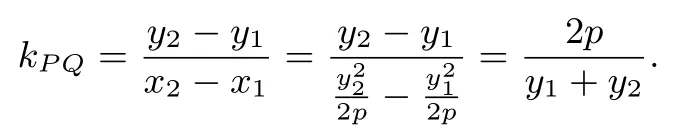
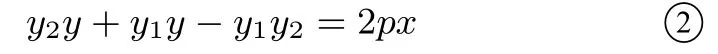
将 ①式中的y1y2代入到 ②式中并整理可得: 直线PQ:(y1+y2)(y+y0)=因此PQ 过定点

(II) 若kPQ不存在, 则P(x1,y1), Q(x1,−y1), kAP=

四、总结反思

圆锥曲线与直线的关系是高考常考的重难点内容,碰到这类问题应多去思考每一道题的本质,这类题目可以如何改编以及解决这类问题的通法.对一个问题的回顾与反思往往比解决这个问题本身更重要,只有真正理解一个问题的本质,才能跳出“题海”的禁锢.