例谈圆锥曲线中计算问题的优化处理*
广东省广州市增城区增城中学(511300) 邓 城
一、问题的提出
在解析几何问题中,经常会出现方法有了,但却难以计算下去的问题.不可否认有些解析几何的题目计算量本身就比较大,但一般来说高考题和大部分省市的模拟题都是会控制纯计算的难度的,出现计算不下去的原因主要是解题思路不够合理、运算方法不够优化.而要提升学生的数学运算素养应基于学生的基本活动经验,选择有代表性的、难度适中的题目让学生尝试从多角度思考运算问题的优化处理.下面笔者选取教学实践中碰到的案例进行剖析,借此抛砖引玉.
二、案例的剖析
例1(2017年郑州市模拟考试)已知双曲线的左、右焦点分别为F1,F2,过F1作圆x2+y2=a2的切线分别交双曲线的左、右两支于点B、C,且|BC|=|CF2|,则双曲线的渐近线方程为( )
A.y =±3x B.y =±2x
分析先来看看下面这种网上看到的参考解法.因为过F1作圆x2+y2=a2的切线分别交双曲线的左、右两支于点B、C, 且|BC|=|CF2|, 所以|BF1|=2a.设B(x,y),则利用三角形的相似可得所以所以代入双曲线方程,整理可得所以双曲线的渐近线方程为
这个方法看上去挺常规的,可以说前半部分求出B 点坐标的方法是非常简捷的,而将B 点坐标带入双曲线方程进而确定a 与b 的关系似乎也是常见的方法.然而真正亲自计算后却发现非常复杂,很难算出答案来! 事实上将圆锥曲线上的点先用其它条件表示出来,然后代入曲线的方程,这种方法有时存在计算难度增加的风险,比如本题中B 点坐标已经出现了较为复杂的分式形式,代入曲线方程时还要进行平方和除法等运算,导致出现高次方程,可以说是人为增加了计算难度.所以从优化计算的角度出发,应尽量避免代入圆锥曲线方程.此时应引导学生注意到: 将点代入曲线方程的本质就是相当于使用了点在曲线上这个核心条件,那么其替代方案可以是使用圆锥曲线的第一定义或第二定义.
而应用第一定义处理则有如下过程:
由|BF2|−|BF1|=2a 得2a=2a,化简得4a2b2+4a4=16a2(a2+b2),4c4−8c2ab=12a2(a2+b2),或(舍去),此解法的计算量要比用第二定义的解法要大一些,但还是比原解法要靠谱些.
例2已知椭圆= 1(a > b > 0)经过点一个焦点是F(0,−1).
(1) 求椭圆C 的方程.
(2) 设椭圆C 与y 轴的两个交点为A1,A2(A1在A2上方),点P 在直线y=a2上,直线PA1,PA2分别与椭圆C交于M,N 两点.试问: 当点P 在直线y=a2上运动时,直线MN 是否恒过定点Q? 证明你的结论.
分析本题的难点在于第二问.证明直线是否过定点问题属于圆锥曲线中的经典问题,并且往往有几种解法,然而在不同的题目条件下,不同解法之间的难度是不一样的,在教学中应引导学生充分体会各种解法的适用性,学会根据具体条件选择合适的解法.为了让学生有更加深入的对比,可以先展示更为基础却又十分经典的一道题.
题目已知抛物线C 的方程为y2=4x,过原点O 作两条相互垂直的直线分别与抛物线C 交于A、B 两点,试问直线AB 是否恒过一定点Q?
思路1先表达出A、B 两点的坐标, 再表达出直线AB 的方程, 然后通过方程判断直线AB 是否经过一个定点.解答如下: 由题意可知直线OA、OB 的斜率存在, 设直线OA 的斜率为k, 则OB 的斜率为=kx,联立解得同法解得B(4k2,−4k), 所以故可得直线AB 的方程为整理可得所以直线AB 恒经过点Q(4,0).
思路2同上法解得同法解得B(4k2,−4k),接下来先缩小点Q 的范围, 考虑到当k=1 时, A(4,4),B(4,−4), 直线AB 的方程为x=4, 若直线AB 恒过一定点Q, 则Q 点坐标可设为(4,m), 且kQA=kQB, 即得解得m=0,所以直线AB 恒经过点Q(4,0).
思路3先表达出直线AB 的方程为x=my+c,然后利用已知条件寻找直线方程中参数的关系,从而证明AB 恒过一定点Q.设直线AB 的方程为x=my+c, A(x1,y1),B(x2,y2),联立得y2−4my−4c=0,所以y1y2=−4c,x1x2=因为直线OA 与直线OB 相互垂直, 所以即有x1x2+y1y2=0,整理得c2−4c=0, 所以c=4, 所以直线AB 恒经过点Q(4,0).
从上述三种思路的计算量来看, 思路3 的计算量最小,思路1 和思路2 的计算量稍微大些,但由于本题中涉及的圆锥曲线是方程形式比较简单的抛物线, 而且条件OA⊥OB也比较简单,所以在本题中这三种思路没有难度上的本质区别,只要能熟练应用都可以.
回到例2,如果先表达直线MN 的方程为y=kx+n,由于寻找直线参数k 与n 的关系要借助联立直线与椭圆后使用韦达定理,而x1x2与x1+x2的关系在本题中是不容易找到的,不妨让学生先试下,然后再展示完整的解答过程:
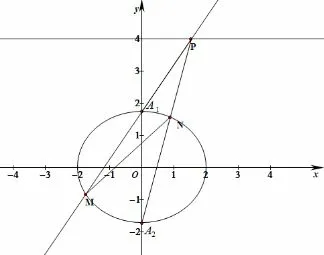
图1
解法1
(2) lMA1:因为P 在lMA1上,所以

lNA2:因为P 在lNA2上,所以
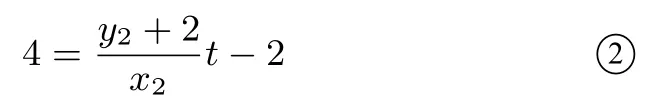
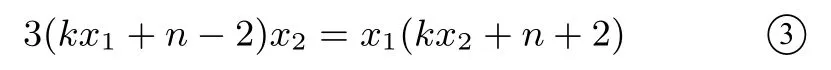
不难发现,此法能够做出来靠的是巧妙的变形技巧,对于大部分基础一般的学生来说难以领悟和应用,所以碰到难以直接找到x1、x2关系的题目不适宜选择先表达目标直线方程再找参数关系的方法.
下面再展示网上提供的一种解法:
解法2直线MN 恒经过定点Q(0,1).证明如下:
当直线MN 斜率不存在时,直线MN 即y 轴,通过点Q(0,1).当点P 不在y 轴上时,设M(x1,y1)、N(x2,y2),则直线PA1方程:直线PA2方程:联立得(3+t2)x2+6tx=0,解得所以联立得(27+t2)x2−18tx=0,解得所以所 以所以直线MN 恒经过定点Q(0,1).
这种解法目标清晰,并且计算量较少,然而对于学生来说一定有个疑问: 怎么一开始就知道点Q 的坐标是(0,1)呢? 事实上这是本解法的关键之处,作为答案不给出来Q 点坐标的来由并没有什么问题,因为后面确实证明了直线MN恒经过这个Q 点,但在解题教学中,学生有了疑问就有了真正学习的可能,教师不应急着展示自己的“厉害”,而应设计好问题,让学生自己先尝试分析和讨论.
师: 如果直线MN 恒经过这个Q 点,能否缩小Q 点的范围?
学生通过类比前面问题所涉及到的缩小点范围的技巧, 不难发现当点P 移动到y 轴上时, 直线MN 即y 轴, 所以所过定点Q 必在y 轴上.不妨设Q(0,m), 同解法2 得由kQM=kQN得化简得(36+4t2)(m−1)=0, 所以m=1, 所以直线MN 恒经过定点Q(0,1).
从特殊情况缩小定点的可能位置,进而减少未知量,达到简化运算的效果,这是教学中需要重点强调的思路和方法,应尽量让学生感悟这种基本活动经验.
另外,如果学生的学习基础较好,还可以从更深层次的极点极线知识的角度让学生尝试探究下Q 点位置,激发学生对圆锥曲线规律性质的好奇心和学习兴趣.
例3已知椭圆A、B 是椭圆上的两个点,且直线PA,PB 的斜率之积为求证:直线AB 恒过定点,并求出该定点的坐标.
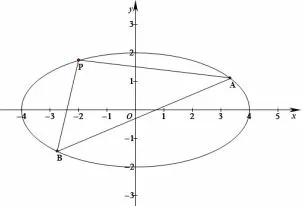
图2
分析此题虽然也是恒过定点问题,但认真分析条件却可以发现有几个不同,解题教学中应充分让学生对比发现差异所在.
师: 能否先缩小直线AB 恒过定点的位置范围?
生: 由于P 的位置较为一般,且直线PA,PB 的斜率之积为也是一般性条件,难以通过特殊化方法缩小定点的位置范围.
师: 先利用已知条件先把A、B 两点的坐标表示出来如何?
生: 由于P 的坐标不够特殊,通过联立直线PA 的方程和椭圆方程求解A 点坐标的计算过程非常繁琐(求B 的坐标同样如此).
可见,此题不宜像例2 的解法2 一样处理,注意到题目中的“直线PA,PB 的斜率之积为这个条件,可考虑采用例2 中解法1 的思路,将直线AB 的方程用y=kx+m表示出来,再借助斜率之积的条件寻找参数k 与m 的关系,进而确定直线所过定点.
解法1设直线AB 的方程为y=kx+m,代入椭圆方程,得(4k2+1)x2+8kmx+4m2−16=0,x1+x2=整理得(2k2+化简得4k2−8km+3m2−配方得所以当时,直线AB 的方程y =kx+m 可化为直线AB 恒过定点当时,直线AB 的方程y =kx+m可化为直线AB 恒过定点此即为P 点,这种情况不合题意.综上所述,直线AB 恒过定点
上述的解法目的明确,思路清晰,虽然计算量略大,但也在高考计算量范围之内,那么能否进一步优化计算方法? 事实上,在学生的接受能力许可的条件下,可以考虑提供齐次化处理方法:
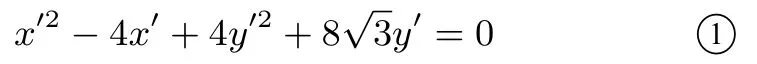
设直线AB 的方程为

利用 ②式将 ①式齐次化,得
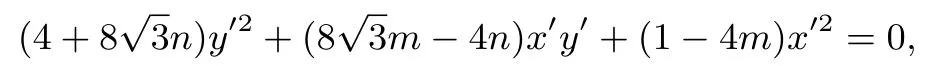
同除x′2得,
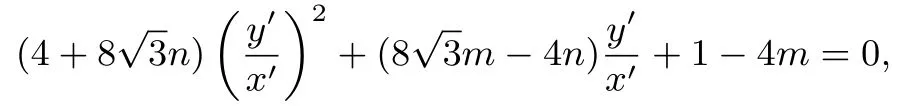
此时
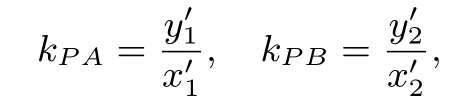
三、案例的总结
从上面的几个案例不难发现,解析几何中的运算问题不是纯粹的代数运算问题,而是涉及到如何利用圆锥曲线中的几何条件进行合理的转化和表达的问题.例1 表明在利用点在圆锥曲线上这个条件时,不一定将点的坐标直接代入曲线的方程,而应该评估下点的坐标的复杂程度,如果点的坐标已经比较复杂时代入曲线的方程会导致运算更加复杂繁琐,此时可以借助圆锥曲线的第一定义或第二定义.例2 和例3则表明优化动直线过定点问题的运算应从实际条件出发,如果能够将核心条件转化为两根之和和两根之积的条件,则可以先设出动直线的方程y =kx+m(或者是x=ky+m)再寻找k 与m 的关系,进而求出动直线所过的定点坐标.否则应考虑将动直线与圆锥曲线的两个交点表达出来,接着通过动直线的动态变化规律缩小定点的范围,然后再利用三点共线的条件求出定点的具体坐标.

