活跃在高考解题中的罗尔定理

安徽省无为第三中学城北校区(238300) 朱小扣

广东省兴宁市第一中学(514500) 蓝云波

罗尔定理是微分学中一条重要的定理,与拉格朗日中值定理、柯西中值定理并称为是三大微分中值定理.而高考中的导数题有时仅仅依靠高中课本知识很难解决,很多时候会用到高等数学里的知识,如函数极限的定义,洛必达法则,拉格朗日中值定理,琴生不等式等知识,本文将围绕罗尔定理在解决一类高考题中的运用展开阐述,以期抛砖引玉.

1.罗尔定理的引入

如果函数f(x)满足以下条件: (1)在闭区间[a,b]上连续,(2)在开区间(a,b)内可导,(3)f(a)=f(b),则至少存在一个ξ ∈(a,b),使得f′(ξ)=0.

2.罗尔定理的运用

例1(2016年广东省高三适应考试21 题改编)已知函数求证: 函数f(x)只有一个零点.

证明① 先证存在性.由及得由零点定理得: 至少存在一个实数使得f(c)=0.

② 再证唯一性.假设f(x) 有两个零点, 设为x1,x2(0 < x1< x2),则f(x1)=f(x2)=0,由罗尔定理得: 至少存在一个a ∈(x1,x2),使得f′(a)=0,即这与

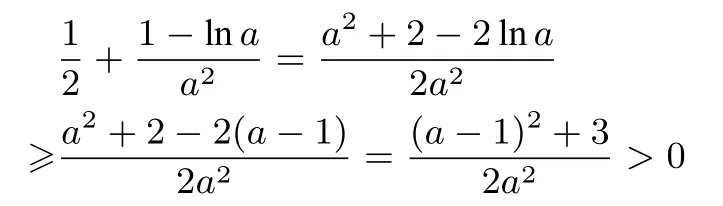
相矛盾,故假设不正确.

综合 ① ②得: 函数f(x)只有一个零点.

点评由罗尔定理可以解决有关函数零点个数的问题或方程根的个数问题,是有别于用函数单调性讨论零点的另一种方法,使用起来简单,便于学生掌握.

例2(2014年四川卷理21 题) 已知函数f(x) =ex−ax2−bx−1, 其中a,b ∈R, e=2.71828··· 为自然对数的底数.

(1) 设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;

(2) 若f(1)=0,函数f(x)在区间(0,1)内有零点,求a的取值范围.

解析(1) 略.(2) 因为f(x)=ex−ax2−bx−1, 所以g(x)=f′(x)=ex−2ax−b, 又g′(x)=ex−2a, 由f(1)=0⇒e−a−b−1=0⇒b=e−a−1.设x0是f(x)的零点且x0∈(0,1),则f(0)=f(x0)=f(1)=0,由罗尔定理得:在(0,1)上有两个不同的解, ⇒g(x)=0 在(0,1) 上有两个不同解.易知当或时,函数g(x)即f′(x)在区间[0,1]上单调,不可能满足g(x)=0 在(0,1)上有两个不同解.若则

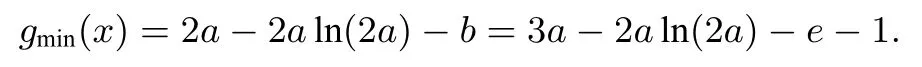
令

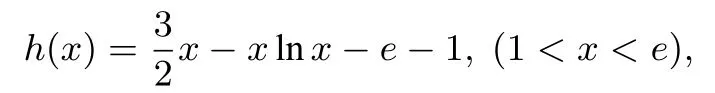
点评本题第一问考察分类讨论思想, 第二问通过罗尔定理能迅速找到解题的突破口, 但注意不能用罗尔定理两次按如下思路去解答:⇒f′′(x)=0 在(0,1)上有解(注: 错误思路)以上思路是错误的,因为连续用两次罗尔定理会改变(扩大)范围.

例3(2018年巴蜀中学高三1 月) 已知函数f(x) =e−x·(2mx2+nx+1).

(I) 若x=1 和2 是函数f(x) 的两个极值点, 求曲线y =f(x)在点(0,f(0))处的切线方程;

(II) 若f(1)=1,则方程f(x)=1 在(0,1)内有解,求m 的取值范围.

解析(I) 切线方程是y =−2x+1(过程略).

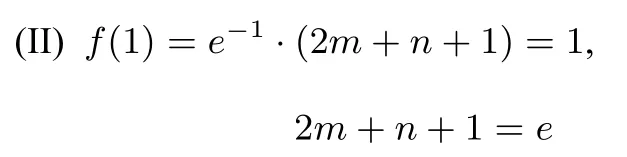
f(x)=e−x·(2mx2+nx+1)=1,(2mx2+nx+1)=ex.令g(x)=ex−2mx2−nx−1,则g(x)在(0,1)内有零点.设x0为g(x)在(0,1)内的一个零点,则g(0)=g(x0)=g(1)=0,则由罗尔定理知⇒g′(x)=0在(0,1) 上有两个不同的解.令h(x)=g′(x), 则g′(x) =ex−4mx−n,h′(x)=ex−4m,当h(x)在(0,1)区间上递增,h(x)不可能有两个及以上零点;当时,h′(x) < 0,h(x)在(0,1)在区间上递减,h(x)不可能有两个及以上零点;当时,令h′(x)=0,得x=ln(4m) ∈(0,1), 所以h(x) 在区间(0,ln(4m)) 上递减, 在(ln(4m),1) 上递增, h(x) 在区间(0,1) 上存在最小值h(ln(4m)), 若h(x) 有两个零点, 则有h(ln(4m)) < 0,h(0)>0,h(1)>0,

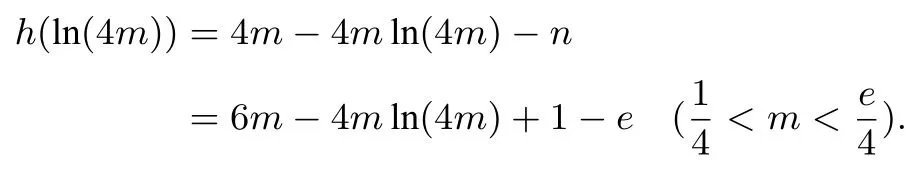
设

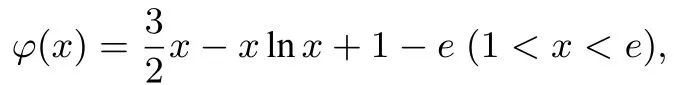
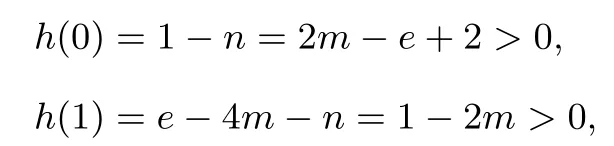
以上用罗尔定理出题的思路,多次出现在高考模拟题中,又如:

例4(2018年衡水金卷理数一) 已知函数f(x) =ex−2(a−1)x−b,其中e 为自然对数的底数.

(1) 若函数f(x)在区间[0,1]上是单调函数,试求实数a 的取值范围;

(2) 已知函数g(x)=ex−(a−1)x2−bx−1,且g(1)=0,若函数g(x)在区间[0,1]上恰有3 个零点,求实数a 的取值范围.

解析(1) f(x)=ex−2(a−1)x−b, 当函数f(x)在区间[0,1] 上单调递增时, f′(x)=ex−2(a−1)0在区间[0,1] 上恒成立, 故2(a−1)(ex)min=1 (其中解得当函数f(x)在区间[0,1]上单调递减时,f′(x)=ex−2(a−1)0 在区间[0,1]上恒成立,故2(a−1)(ex)max=e(其中0x1),解得综上所述,实数a 的取值范围是

(2) g′(x)=ex−2(a−1)x−b=f(x).由g(0)=g(1),知g(x) 在区间(0,1) 内恰有一个零点, 设该零点为x0, 则由罗尔定理知在(0,1)上有两个不同的解,即f(x)=0 在(0,1)上有两个不同的解.

令f(x)=0,得x=ln(2a−2)∈(0,1),所以函数f(x)在区间[0,ln(2a−2)] 上单调递减, 在区间(ln(2a−2),1]上单调递增.记f(x) 的两个零点为x1,x2(x1< x2),因 此x1∈ (0,ln(2a−2)), x2∈ (ln(2a−2),1), 必 有f(0)=1−b > 0,f(1)=e−2a+2−b > 0.由g(1)=0,得a+b=e,所以

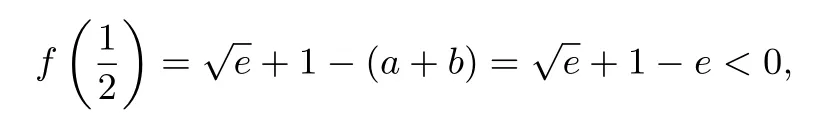
又f(0)=1−b > 0, f(1)=e−2a+2−b > 0, 所以e−1

点评例3 和例4 都是例2 的模仿题,思路基本一致,但模仿中带有传承与创新.像这些“难题”,解答过程十分繁多,学生在一开始,不可能一次就能写出完整的解答.只有知道和熟练的利用罗尔定理,才能在考试的有限时间中,找到合理的思路,从而给出合理的解答.

总结解决导数题目时,除了用罗尔定理外,有时也会用对数平均不等式,琴生不等式,拉格朗日中值定理等知识.这些“超纲”的知识,我觉得学生还是有必要掌握一些的,因为它可以帮助你迅速找到解题的思路与方法,使得问题迅速化归并解决.“小知不及大知”,只有不断增加自己的数学涉猎,才能秒杀此类题.