2018年高考全国I卷理科第21题的解法探究
广东省湛江一中培才学校(524037) 魏 欣 林俊杰
2018年高考全国I卷理科第21题集函数、导数、不等式于一体,是一道既具有一定的基础性与综合性,渗透着分类讨论、数形结合和等价转化的思想方法,全方位考查了学生的观察、分析、推理论证、运算求解的数学能力.本文主要针对第(II)问,从不同的视角进行分析,以便有效把握试题,有效突破导数压轴题.
一、真题展示
(I)讨论f(x)的单调性;
(II)若f(x)存在两个极值点x1和x2,证明:.
二、试题分析
本题属于传统题,考查了函数的单调性和证明不等式问题.以含参数不等式问题为载体,既考查学生的分类讨论思想、等价转化思想、数形结合思想和函数方程及不等式思想,又考查学生分析问题和解决问题的能力.本题由浅人深,对计算难度、思维深度的要求逐步提高,很好地体现了数学的科学性、应用性和创造性.
三、解法探究
解析(I)f(x)的定义域为(0,+∞),
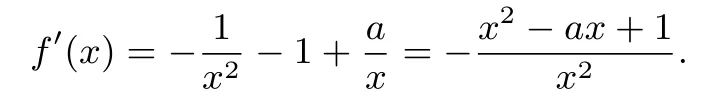
设方程x2−ax+1=0的判别式为∆,∆=a2−4;
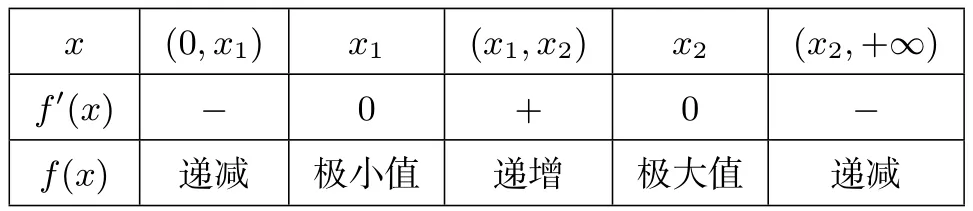
①当∆=a2−4>0时,设方程x2−ax+1=0的两个根为x1、x2,则有x1+x2=a,x1·x2=1.
?
所以f(x)在(0,x1),(x2,+∞)上单调递减,f(x)在(x1,x2)上单调递增.
②当∆=a2−40时,即当−2a2时,f′(x)0,所以f(x)在(0,+∞)上单调递减.
综上所述,当a>2时,f(x)在(0,x1),(x2,+∞)上单调递减,f(x)在(x1,x2)上单调递增;当a2时,f(x)在(0,+∞)上单调递减.
对于第(II)问有以下六种求证方法.
方法一由(I)可知
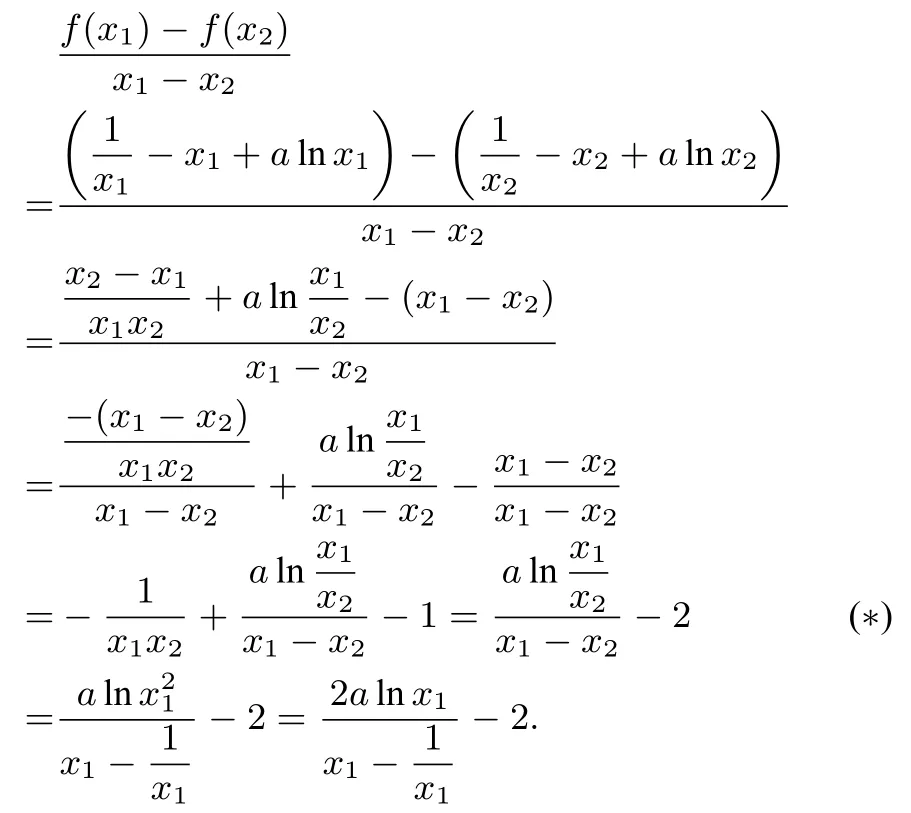
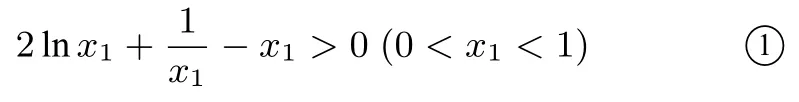
构造函数
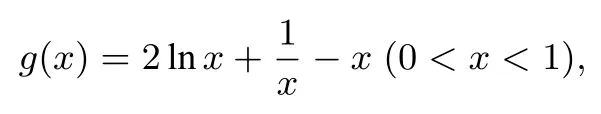
则

方法二由(I)可知0
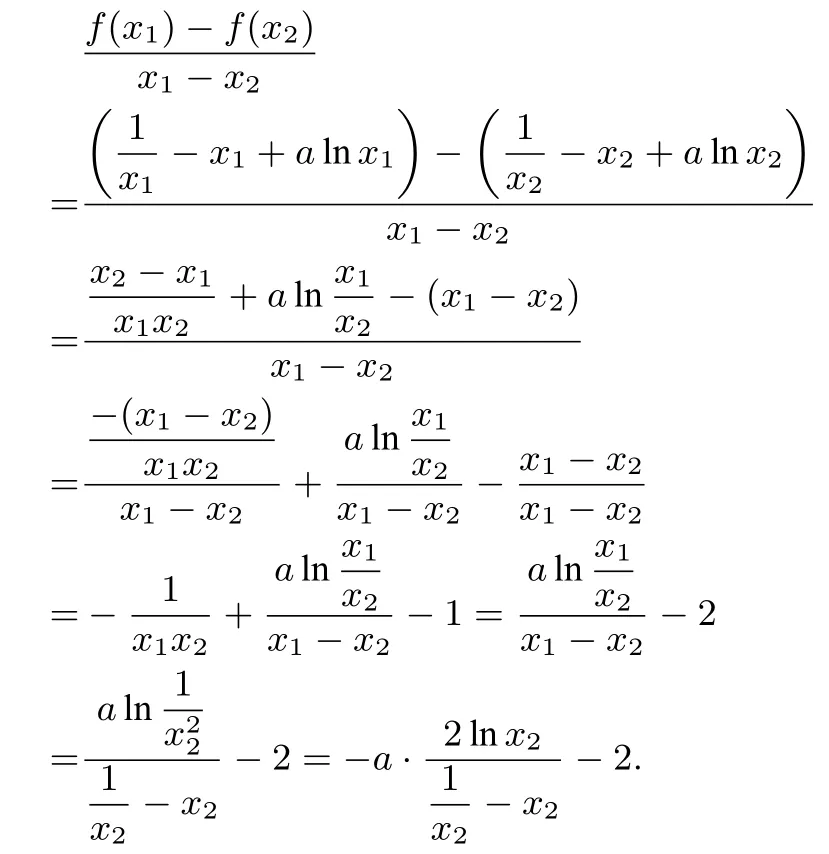
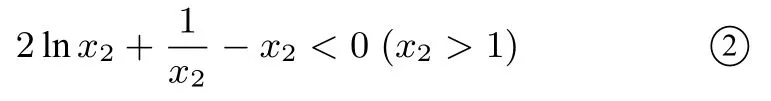
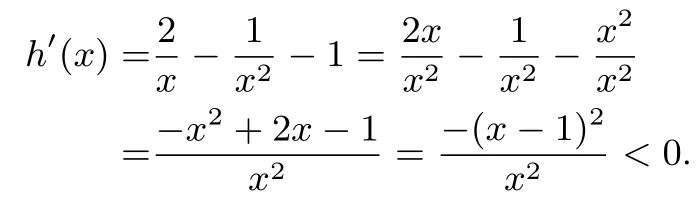
评注(1)构造函数运用导数判断函数单调性是基本而常用的方法;(2)利用x1,x2的对等性即有方法一和方法二.
方法三由(I)可知0
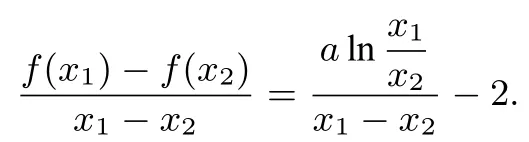
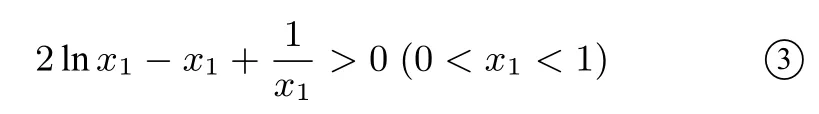
又因为0 构造函数g(x)=2xlnx−x2+1(0 所以g′(x)在(0,1)上单调递增,g′(x) 评注构造函数运用导数判断函数单调性时关键是根据解题需要和已知信息构造出适合的函数. 方法四由(I)可知0 又因为0 方法五由(I)可知0 又因为0 评注解析一到解析五都运用了构造函数,然后求导判断函数单调性的方法,由于解题的切入点不同,构造的函数各异,解题的难易也有别,请同学们进行解题比较与解题分析.本文给出了2018年高考全国I卷理科第21题第(II)问的五种基本解法,这些解法也是解决该类问题的最常用的方法(尤其构造函数,二次求导等),请同学们在学习(分析和比较)以上解法的基础上探讨该题的其它解法,通过解题学解题,多总结、勤反思,源源不断地开发出自己的解题智慧. 方法六对数平均不等式法 证明(万能t法)不妨设0 评注由以上解法我们可以看到,一个新的平均不等式——对数平均不等式可以应用到我们的高考题中,尽管在教材中对这个不等式未曾提起,但是在高考试题中,以这个不等式为背景的压轴题已屡见不鲜,给所有高中数学老师和高三考生一种“一切尽在不言中”的感觉,虽然我们无法猜测高考命题者的初衷及试题的实际背景,但是在高考备考过程中,提出对数平均不等式的背景还是挺有意义的. 由以上利用构造函数法和对数平均不等式的解法不难发现,在2017、2016、2015年全国I卷文理科导数压轴题、2012年辽宁卷理科的压轴题、2011年湖南卷文科第22题、2013年全国卷I理科第21题等等,也均可以用以上解法,体现了高考试题“常考常新,推陈出新”的理念.均可以用上述的通性通法来解答,由于篇幅关系,此处只做简析. 利用构造函数法或对数平均不等式解答高考导数压轴题一般得通性通法有以下步骤: 1.求导数之前首先要指明定义域;2.画初等函数图像时要考虑单调、定点、零点、极限等问题;3.构造函数,分类讨论应先讨论简单的,从易到难,步步深入.通过研究不难发现,构造函数优化解法既简单又快捷,而且不容易出错.它的优点在于:①复杂的问题简单化,即把一个复杂的问题,分解为一系列简单的问题.②一般的问题特殊化,有些一般的结论,找不到一般解法,先看特殊情况,先找出结论,再慢慢求解. 平时注重一题多解、一题多变的训练是解决此类问题的好帮手.一题多解有利于提高学生思维的发散性、灵活性,能激发学生的学习兴趣,对于学生从不同角度、不同侧面去分析问题、解决问题,对于调动解题积极性,培养发展思维,创造性品质有着重要的意义.

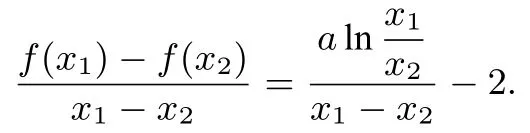
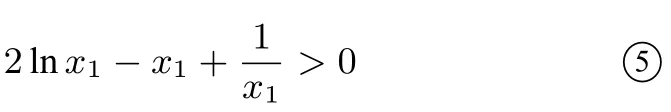

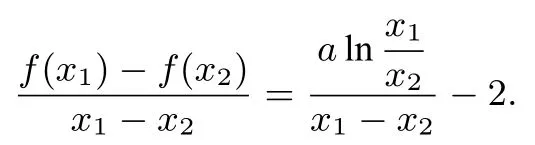
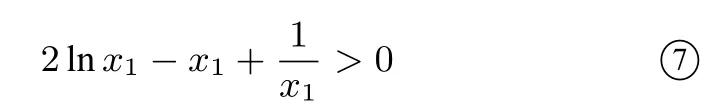

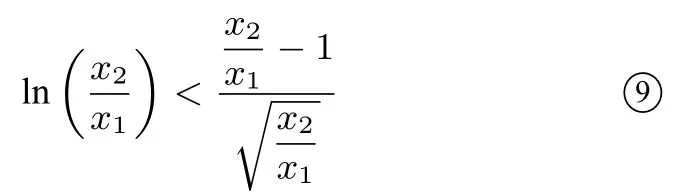
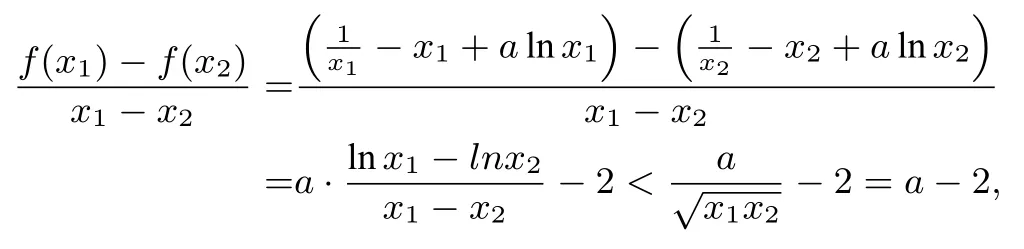
四、真题回顾
五、备考建议

