柯西不等式的多视角证明及应用

陕西省商洛市洛南县西关中学(726100) 冀建军 王 伟

柯西不等式是高考必考内容和高频考点,运用柯西不等式解决相关求值、不等式证明、求最值等问题可以起到事半功倍的效果.学生对柯西不等式大多停留在识记公式层面,能进行直接应用,但遇到具体问题情境,意识不到用柯西不等式,不能进行知识迁移,束手无策,只能放弃,其关键是对公式内涵理解不够,对公式相关变形及几何意义达不到“创新型理解”.

1.柯西不等式的形式

柯西不等式一般形式为:设ai,bi∈R,则即对于(a1b1+a2b2+···+anbn)2,当且仅当ai=kbi时等号成立.

(a2+b2)(c2+d2)(ac+bd)2,当且仅当时等号成立.

1.1 基本不等式是柯西不等式的特殊形式

对任意a、b∈R,由柯西不等式有,(a2+b2)(b2+a2)(ab+ba)2,即a2+b22ab.由(12+12)(a2+b2)(a+b)2,即可得

当a、b∈R+时,即或者即即当且仅当a=b时等号成立.由可得,即

1.2 柯西不等式的实质

柯西不等式反映的是任意两组实数ai、bi(i=1,2,···n),其对应项“相乘”之后“求和”再“平方”这三种运算不满足交换律,即先各自“平方”之后“求和”再“相乘”,运算的结果不会变小[1].

1.3 柯西不等式的几何解释

图1

2.柯西不等式的证明

证明过程是揭示各个量之间关系的过程,是对不等式内涵以及交融知识的理解.以二维柯西不等式(a2+b2)(c2+d2)(ac+bd)2的证明为例.

2.1 不等式证明视角

证法1(作差比较)

(a2+b2)(c2+d2)−(ac+bd)2=(ad−bc)20,当且仅当ad=bc时等号成立,即证.

证法2(作商比较)

证法3(综合法)

(a2+b2)(c2+d2)=(ac+bd)2+(ad−bc)2(ac+bd)2,当且仅当ad=bc时等号成立,即证.

证法4(分析法)

要证(a2+b2)(c2+d2)(ac+bd)2,即证a2d2+b2c2−2abcd0,即证(ad−bc)20,当且仅当ad=bc时等号成立.

证法5(反证法)

假设(a2+b2)(c2+d2)<(ac+bd)2成立,即(ad−bc)2<0,这不可能,即假设错误,原不等式成立.

2.2 向量视角

证法6设则而则有此时等号成立条件是共线.此法也适宜于证明n维柯西不等式.

2.3 函数方程视角

证法7当a,b全为0时,不等式显然成立.当a,b不全为0时,类比一元二次方程判别式结构,构造函数f(t)=(a2+b2)t2+2(ac+bd)t+(c2+d2),由于对任意t∈R,f(t)=(at+c)2+(bt+d)20,则[2(ac+bd)]2−4(a2+b2)(c2+d2)0,即(a2+b2)(c2+d2)(ac+bd)2,当且仅当f(t)=0时,即(at+c)2=(bt+d)2=0,此时时等号成立,即证.

若令f(t)=(a1t+b1)2+(a2t+b2)2+···+(ant+bn)20,可证n维柯西不等式的一般形式.

证法8设a2+b2=m0,c2+d2=n0,则即ac+bd即证.

2.4 解析几何视角

证法9如图2,设A(a,b),表示B(c,d)到直线ax+by=0的距离,由于过原点与直线OA垂直的直线方程为ax+by=0,且点B到直线ax+by=0的距离不大于|OB|,即即当且仅当O、B、A三点共线即时等号成立.

图2

2.5 复数视角

证法10设z1=a+bi,z2=c+di,则z1z2=(ac−bd)+(ad+bc)i,由于|z1z2|=|z1|·|z2|=同 时即:即(a2+b2)(c2+d2)(ac+bd)2,当且仅当ad=bc时等号成立.

3.柯西不等式的应用

3.1 利用等号成立条件求值

例1已知x,y,z∈R,且满足x2+y2+z2=1,x+2y+3z=求x+y+z的值.

解由柯西不等式:(x+2y+3z)2(x2+y2+z2)(12+22+32),即(x+2y+3z)214(x2+y2+z2),根据题设等号成立,则代入可求,即即

例2已知x,y,z,a,b,c∈R+,且x2+y2+z2=40,a2+b2+c2=10,ax+by+cz=20,求的值.

解由已知,(ax+by+cz)2=(x2+y2+z2)(a2+b2+c2)=400,而x,y,z,a,b,c∈R+,根据柯西不等式,(ax+by+cz)2(a2+b2+c2)等号成立条件为则(a2+b2+c2)=k2(x2+y2+z2),即10=40k2,即故

例3解方程

解利用柯西不等式有

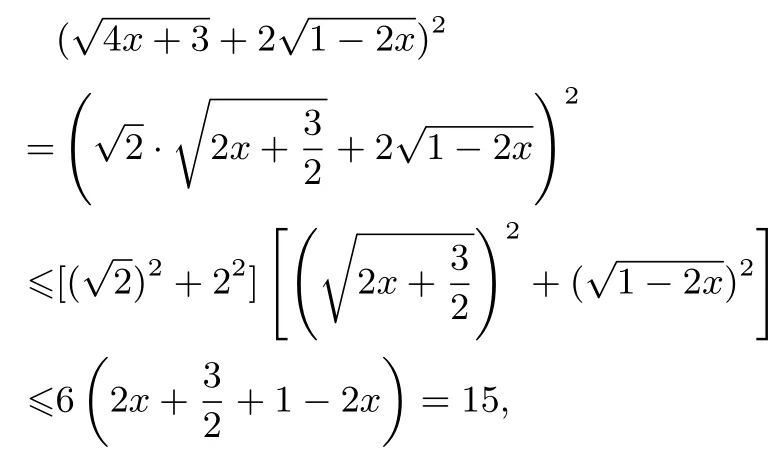
评注例1中三个变量两个方程,常规方法不易直接求x,y,z旳值;例2中虽三个变量三个方程,但有交叉项;例3可采取移项两次平方求解,运算麻烦,但利用柯西不等式等号成立条件求解简捷方便.例3中也可运用目的配凑消去x.

3.2 利用柯西不等式证明

例4已知a,b,c都是正数,且a+b+c=1,求证:

证明由柯西不等式知,

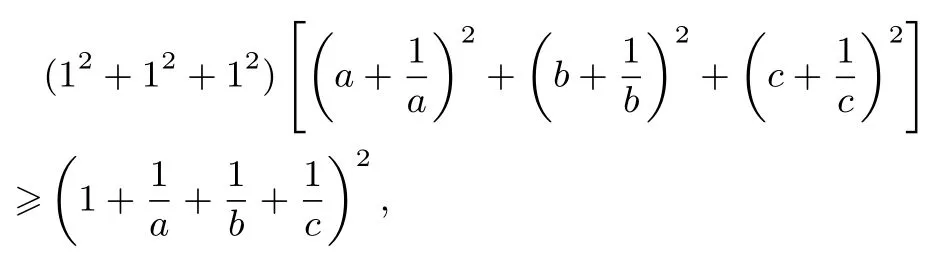
即

又

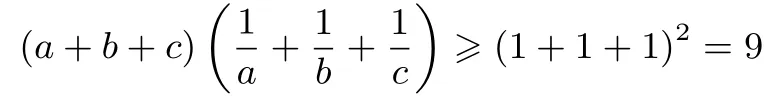
当且仅当a=b=c时取等号.

评注运用柯西不等式关键是“配凑”形式,充分利用已知条件.当出现分式和的形式时,一般构造分式分母和作为因式.

3.3 利用柯西不等式求最值

例5设x,y∈R,若4x2+xy+y2=1,则2x+y的最大值____.

解4x2+xy+y2=1即由柯西不等式(2x+y)2,即

评注有交叉项xy,以x为主元,构造平方和形式.要出现2x+y,给乘以1,给乘以得到相加即得.

例6设a,b,m,n∈R,且a2+b2=5,am+bn=5,则的最小值为____.

解法1设点A(m,n),由am+bn=5知,点A(m,n)在直线ax+by=5上,而最小即OA的最小值.由垂线段最短知,当且仅当OA与直线ax+by=5垂直即an=bm时取最小值.

解法2由柯西不等式,(a2+b2)(m2+n2)(am+bn)2,即当且仅当时等号成立.

评注解法1也是对解法2的推导和解释.

例7设a,b,c∈R,且a+b+c=2,a2+2b2+3c2=4,求a的取值范围.

解分离变量a,由a+b+c=2即得b+c=2−a,由a2+2b2+3c2=4即得2b2+3c2=4−a2,由柯西不等式有:即5(4−a2) 6(2−a)2,即

评注在多变量关系中,求一个变量的取值范围,可先将目标变量分离,再运用柯西不等式通过非目标变量关系构建目标变量的关系.

柯西不等式是解决多变量关系的利器,反映了两组实数“先平方后求和再求积”与“对应项之积求和再平方”的关系,要通过从不同视角对不等式的证明领悟柯西不等式在交融知识的应用,能在具体问题情境中应用柯西不等式简化问题的解决过程.