2019年美国数学竞赛(AMC10B)的试题与解答

广东省华南师范大学数学科学学院(510631) 李湖南

本试题是2019年美国中学数学竞赛(高一年级)在中国考试统一使用的B 卷.

1.Alicia had two containers.The first wasfull of water and the second was empty.She poured all the water from the first container into the second container, at which point the second container wasfull of water.What is the ratio of the volume of the smaller container to the volume of the larger container?

解: 设第一、二个容器的容积分别为V1和V2,依题意有从而故(D)正确.

2.Consider the statement,”If n is not prime,then n−2 is prime.”Which of the following values of n is a counterexample to this statement?

(A) 11 (B) 15 (C) 19 (D) 21 (E) 27

译文: 考虑陈述“若n 不是素数,则n−2 是素数.”以下哪个值n 是这个陈述的一个反例?

解: 反例是指符合命题的条件但不符合命题的结论的例子,即满足“若n 不是素数,则n−2 是素数.”选项中只有27满足,故(E)正确.

3.In a high school with 500 students, 40% of the seniors play a musical instrument, while 30%of the non-seniors do not play a musical instrument.In all, 46.8% of the students do not play a musical instrument.How many non-seniors play a musical instrument?

(A) 66 (B) 154 (C) 186 (D) 220 (E) 266

译文: 在一所有500 名学生的高中里,40%的高年级学生会演奏乐器,而30%的非高年级学生不会演奏乐器.总的来说,46.8%的学生不会演奏乐器.问有多少名非高年级学生会演奏乐器?

解: 设非高年级学生有x 名, 则有(1−40%)(500−x)+30%·x=500×46.8%, 解得x=220, 所求学生为220×(1−30%)=154 名,故(B)正确.

4.All lines with equation ax+by =c such that a,b,c form an arithmetic progression pass through a common point.What are the coordinates of that point?

(A) (−1,2) (B) (0,1) (C) (1,−2) (D) (1,0) (E) (1,2)

译文: 所有方程为ax+by=c 的直线经过一个公共点,其中a,b,c 构成一个等差数列.试给出这个公共点的坐标.

解: 依题意有a+c=2b,即−a+2b=c,因此直线过点(−1,2),故(A)正确.

5.Triangle ABC lies in the first quadrant.Points A,B and C are reflected across the line y =x to points A′,B′and C′,respectively.Assume that none of the vertices of the triangle lie on the line y=x.Which of the following statements is not always true?

(A) Triangle A′B′C′lies in the first quadrant.

(B) Triangle ABC and A′B′C′have the same area.

(C) The slope of line AA′is-1.

(D) The slopes of lines AA′and CC′are the same.

(E) Lines AB and A′B′are perpendicular to each other.

译文: 三角形ABC 位于第一象限.点A,B,C 关于直线y =x 的对称点分别为A′,B′,C′.假设三角形的顶点都不在直线y =x 上,以下哪个命题是不正确的?

解: 对于第一象限中任意一点P(x0,y0), 有x0>0,y0>0,关于直线y =x 的对称点P′(x0,y0)显然也在第一象限,(A)正确;△ABC△A′B′C′,面积当然也相等,(B)正确;设A(x1,y1),则A′(y1,x1),斜率(C) 正确; 同理(D) 也正确; 取A(4,1), B(5,3), 则A′(1,4),B′(3,5),斜率直线AB 与A′B′不垂直,(E)不正确,故答案为(E).

6.A positive integer n satisfies the equation(n+1)!+(n+2)!=440·n!.What is the sum of the digits of n?

(A) 2 (B) 5 (C) 10 (D) 12 (E) 15

译文: 正整数n 满足方程(n+1)!+(n+2)!=440·n!,则n 的各位数字之和是多少?

解: 原方程等价于(n+1)+(n+1)(n+2)=440,解得n=19,故(C)正确.

7.Each piece of candy in a shop costs a whole number of cents.Casper has exactly enough money to buy either 12 pieces of red candy,14 pieces of green candy,15 pieces of blue candy,or n pieces of purple candy.A piece of purple candy costs 20 cents.What is the least possible value of n?

(A) 18 (B) 21 (C) 24 (D) 25 (E) 28

译文: 商店里的每一块糖果的价格都是整数美分.卡斯帕的钱刚好够买12 块红糖,或14 块绿糖,或15 块蓝糖,或n块紫糖.1 块紫糖值20 美分.问n 的最小可能值是多少?

解: 最小公倍数[12,14,15]=420, 卡斯帕的钱一定是420 美分的整数倍,因此最小值为n=420/20=21,故(B)正确.

8.The figure below shows a square and four equilateral triangles, with each triangle having a side lying on a side of the square,such that each triangle has side length 2 and the third vertices of the triangles meet at the center of the square.The region inside the square but outside the triangles is shaded.What is the area of the shaded region?

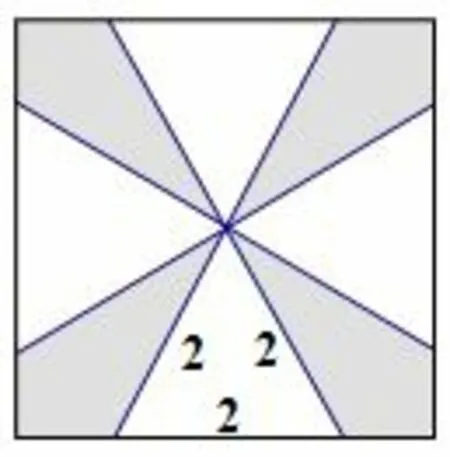
图1

译文: 下图是一个正方形和四个等边三角形,每个三角形的边位于正方形的一条边上,且边长均为2,三角形的第三个顶点在正方形的中心相交.正方形内部但三角形的外部被涂成阴影.问阴影部分的面积是多少?

9.The function f is defined byfor all real numbers x,wheredenotes the greatest integer less than or equal to the real number r.What is the range of f?

(A) {−1,0} (B) the set of nonpositive integers

(C) {−1,0,1} (D) {0} (E) the set of nonnegative integers

10.In a given plane, points A and B are 10 units apart.How many points C are there in the plane such that the perimeter of △ABC is 50 units and the area of △ABC is 100 square units?

(A) 0 (B) 2 (C) 4 (D) 8 (E) infinitely many

译文: 在一个给定的平面上,点A、B 相距10 个单位,则平面上有多少个点C 使得△ABC 的周长是50 个单位且面积是100 个平方单位?

解: 不妨设A(0,0), B(10,0), 由于△ABC 的面积为100, 则点C 到AB 的高为20, 可设C(x,20), 此时,△ABC 的周长为10+20+20=50,故符合条件的点C 不存在,(A)正确.

11.Two jars each contain the same number of marbles,and every marble is either blue or green.In Jar 1 the ratio of blue to green marbles is 9: 1, and the ratio of blue to green marbles in Jar 2 is 8: 1.There are 95 green marbles in all.How many more blue marbles are in Jar 1 than in Jar 2?

(A) 5 (B) 10 (C) 25 (D) 45 (E) 50

译文: 两个罐子里装有相同数量的弹珠,每个弹珠都是蓝色或绿色的.1 号罐中蓝绿色弹珠的比例为9 : 1,2 号罐中蓝绿色弹珠的比例为8:1.总共有95 颗绿色弹珠.问1 号罐子比2 号罐子多几颗蓝色弹珠?

解: 设1 号罐子里的绿色弹珠有x 颗,蓝色弹珠有9x 颗,则2 号罐子里的绿色弹珠有颗,于是解得x=45,从而为所求,故(A)正确.

12.What is the greatest possible sum of the digits in the base-seven representation of a positive integer less than 2019?

(A) 11 (B) 14 (C) 22 (D) 23 (E) 27

译文: 小于2019 的正整数用七进制表示出来的各位数字和的最大值是多少?

解: 由于2018=5×73+6×72+1×7+2, 即2018=(5612)7, 在七进制的表示中, 小于等于5612 的数之数字和最大的为5566 或4666,均为22,故(C)正确.

13.What is the sum of all real numbers x for which the median of the numbers 4,6,8,17,and x is equal to the mean of those five numbers?

译文: 所有使得五个数4,6,8,17 和x 的中位数和平均数相等的实数x 之和是多少?

解: 中位数只可能是6,8 或x: (1) 若中位数是6, 则解得x =−5;(2)若中位数是8,则解得x=5,不符合要求; (3)若中位数是x,则解得也不符合要求.故(A)正确.

14. The base-ten representation for 19! is 121,6T5,100,40M,832,H00 where T,M and H denote digits that are not given.What is T +M +H?

(A) 3 (B) 8 (C) 12 (D) 14 (E) 17

译文:19!的十进制表示为121,6T5,100,40M,832,H00,其中T,M,H 是未知数字.则T +M +H 是多少?

解: 在19!的标准分解式中,有8 个3,3 个5,2 个7,1 个11,1 个13,从而能被9 整除,也能被7×11×13=1001 整除,且尾数上有3 个连续的0,于是H=0;又数字和为33+T+M 能被9 整除,且121+100+832=6T5+40M+H00,解得T =4,M =8.因此T +M +H =12,故(C)正确.

15.Right triangle T1and T2have areas 1 and 2,respectively.A side of T1is congruent to a side of T2,and a different side of T1is congruent to a different side of T2.What is the square of the product of the lengths of the other(third)sides of T1and T2?

译文: 两个直角三角形T1和T2的面积分别为1 和2,T1的一条边等于T2的一条边,T1的另一条边等于T2的另一条边,问T1和T2的第三条边长度之积的平方是多少?

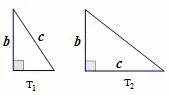
图2

解: 如图示, T1的一条直角边等于T2的一条直角边b, T1的斜边等于T2的另一条直角边c, 则T1的另一条直角边等于的斜边等于依题意有解得所求值为故(A)正确.

16.In △ABC with a right angle at C, point D lies in the interior ofand point E lies in the interior ofso that AC=CD, DE=EB, and the ratio AC : DE=4 : 3.What is the ratio AD :DB?

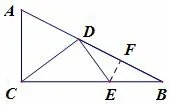
图3

解: 如图示, 过点E 作EF⊥AB 于F, 依题意有∠ADC=∠A, ∠EDB=∠B, 从而∠CDE=180◦−∠ADC−∠EDB =180◦−∠A−∠B =90◦,不妨设AC =CD=4, DE=EB=3, 则BC =CE+EB =8,AB =又由于△BEF△BAC,可得即BF=于是AD :故(A)正确.

17.A red ball and a green ball are randomly and independently tossed into bins numbered with the positive integers so that for each ball,the probability that it is tossed into bin k is 2−kfor k =1,2,3,···.What is the probability that the red ball is tossed into a higher-numbered bin than the green ball?

译文: 一个红球和一个绿球被随机地、独立地抛入用正整数编号的箱子中,每个球被抛入箱子k 的概率为2−k,其中k=1,2,3,···.则红球被抛入比绿球编号更高的箱子的概率是多少?

解: 红球被抛入比绿球编号更高的箱子的概率与绿球被抛入比红球编号更高的箱子的概率是相等的,而红球与绿球被抛入同一个箱子的概率是结果为因此所求概率为(C)正确.

18.Henry decides one morning to do a workout, and he walksof the way from his home to his gym.The gym is 2 kilometers away from Henry’s home.At that point, he changes his mind and walksof the way from where he is back toward home.When he reaches that point,he changes his mind again and walksof the distance from there back toward the gym.If Henry keeps changing his mind when he has walkedof the distance toward either the gym or home from the point where he last changed his mind, he will get very close to walking back and forth between a point A kilometers from home and a point B kilometers from home.What is|A−B|?

译文: 一天早上亨利决定去锻炼,健身房离亨利家2 公里.当他从家里往健身房走到路程的时候,他改变了主意,然后往回走.当他往家里又走了路程的时候,他再次改变主意,然后又往健身房走,而且又走了的路程.如果亨利从他上次改变主意的地方向健身房或家走了距离的时候,不断地改变主意,那么他就可以非常接近地在离家A 公里的一点和离家B 公里的一点之间来回走动了.请问|A−B|是多少?

图4

解: 如图示, 亨利无限地行走下去, 他基本上就会在固定的两个点之间来回.此时有解得从而故(C)正确.

19.Let S be the set of all positive integer divisors of 100,000.How many numbers are the product of two distinct elements of S?

(A) 98 (B) 100 (C) 117 (D) 119 (E) 121

译文: 设S 是100,000 的所有正整数因子的集合,则S中两个不同元素的乘积共有多少个?

解: 100000=25×55, 则S={2i×5j: i,j =0,1,2,3,4,5}, 于是S 中两个元素乘积的集合为{2i×5j:i,j=0,1,2,3,··· ,10},共121 个数.注意到题目要求两个元素不同,所以乘积中要去掉1,210,510,210×510这四个数,剩下117 个,故(C)正确.

20.As showing in the figure,line segmentis trisected by points B and C so that AB=BC=CD=2.Three semicircles of radius 1,AEB,BFC and CGD,have their diameters onlie in the same halfplane determined by line AD,and are tangent to line EG at E,F and G, respectively.A circle of radius 2 has its center at F.The area of the region inside the circle but outside the three semicircles,shaded in the figure,can be expressed in the formwhere a,b,c and d are positive integers and a and b are relatively prime.What is a+b+c+d?

(A) 13 (B) 14 (C) 15 (D) 16 (E) 17

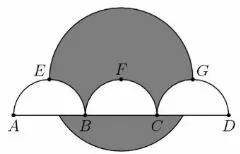
图5

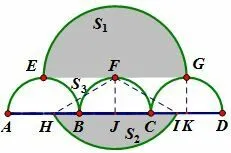
图6

解: 如图示, 设⊙F 与线段AD 相交于点H,I, 取线段BC,CD 的中点分别为J,K, 连结FH,FI,FJ,GK, 则FJKG 是个矩形, 且FJ=GK=1, 从而∠IFJ=60◦,所求阴影部分的面积S=S1+S2+S3,其中S1为⊙F 的上半圆,S2为⊙F 被HI 所截的弓形,S3为其余部分.于是,因此S =即有a=7,b=3,c=3,d=4,得a+b+c+d=17,故(E)正确.

21.Debra flips a fair coin repeatedly,keeping track of how many heads and how many tails she has seen in total, until she gets either two heads in a row or two tails in a row,at which point she stops flipping.What is the probability that she gets two heads in a row but she sees a second tail before she sees a second head?

译文: 黛布拉反复地掷一枚均匀的硬币,记录下她总共看到了多少个正面和多少个反面,直到她连续掷出两个正面或两个反面,这时她就停止.请问她以连续掷出两个正面结束, 但在出现第二个正面之前出现第二个反面的概率是多少?

解: 她至少需要掷5 次才能结束, 此时掷出的结果是01011, 其中0 代表反面, 1 代表正面, 这个结果的概率是当然, 她掷出的结果还可以是0101011, 010101011,……, 概率分别是因此, 所求概率为正确.

22.Raashan,Sylvia,and Ted play the following game.Each starts with$1.A bell rings every 15 seconds,at which time each of the players who currently has money simultaneously chooses one of the other two players independently and at random and gives$1 to that player.What is the probability that after the bell has rung 2019 times, each player will have$1? (For example,Raashan and Ted may each decide to give$1 to Sylvia,and Sylvia may decide to give her dollar to Ted,at which point Raashan will have$0,Sylvia will have$2,and Ted will have$1,and that is the end of the first round of play.In the second round Raashan has no money to give,but Sylvia and Ted might choose each other to give their$1 to, and the holdings will be the same at the end of the second round.)

译文: 拉珊、西尔维娅和特德在玩下列游戏: 开始每人持有1 美元,铃每15 秒响一次,然后每个手上有钱的玩家同时独立、随机地选择另外两个玩家中的一个,并给该玩家1 美元.请问铃响2019 次后,每个玩家仍然持有1 美元的可能性是多少? (例如,拉珊和特德各自决定给西尔维娅1 美元,西尔维娅决定给特德1 美元,第一轮游戏结束,此时拉珊将得到0 美元,西尔维娅将得到2 美元,特德得到1 美元.在第二轮中,拉珊没有钱可给,但西尔维娅和特德可能会选择给对方1 美元,那么第二轮结束时,他们的持有量将不变.)

解: 记拉珊、西尔维娅和特德分别持有的现金m,n,k 美元为(m,n,k), 则在任何时候都有(m,n,k) ∈{(1,1,1),(2,1,0),(2,0,1),(1,2,0),(1,0,2),(0,1,2),(0,2,1)}.

(1)当(m,n,k)=(1,1,1)时,铃响之后,可能出现以下8 种情况:

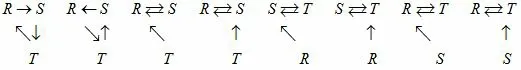
此时的结果分别为(1,1,1),(1,1,1),(2,1,0),(1,2,0),(0,2,1),(0,1,2),(2,0,1),(1,0,2),即一轮过后结果仍然是(1,1,1)的概率为

(2)当三个人持有现金不一样的时候,不妨设(m,n,k)=(2,1,0),铃响之后,可能出现以下4 种情况:

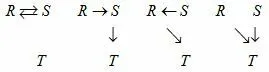
此时的结果分别为(2,1,0),(1,1,1),(2,0,1),(1,0,2), 即一轮过后结果是(1,1,1)的概率为

因此,不管哪种情况,2019 轮过后,结果回到(1,1,1)的概率就是故(B)正确.

23.Points A(6,13) and B(12,11) lie on a circle ω in the plane.Suppose that the tangent lines to ω at A and B intersect at a point on the x-axis.What is the area of ω?

译文: A(6,13)和B(12,11)是平面上的一个圆ω 上的两点.设ω 上的过A 和B 两点的切线相交于x 轴上的同一个点,则圆ω 的面积是多少?

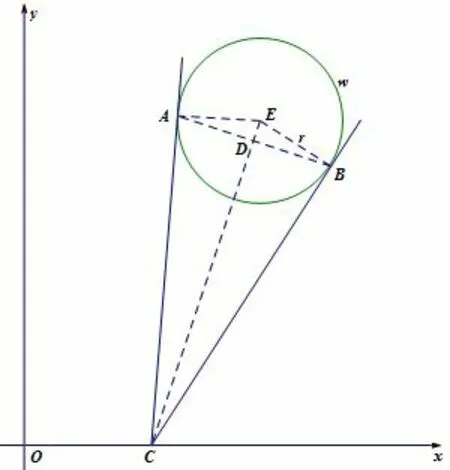
图7

解: 如图示,设圆ω 的圆心为E,半径为r,两条切线交点为C,点C 的坐标为(x,0),连结EA,EB,EC,AB,且AB交EC 于D,依题意有CA=CB,EA=EB,则点E,C 均在AB 的中垂线上,即EC⊥AB,且有AD =DB,于是点D的坐标为(9,12),另外

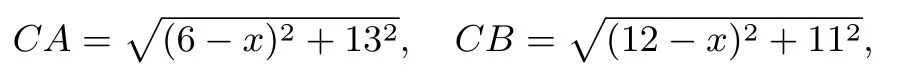
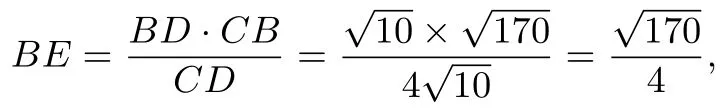
24.Define a sequence recursively by x0=5 and xn+1=for all nonnegative integers n.Let m be the least positive integer such thatIn which of the following intervals does m lie?

(A) [9,26] (B) [27,80] (C) [81,242] (D)[243,728] (E) [729,+∞)

译文: 定义递归数列如下: x0=5, xn+1=∀n ∈N.令m 是使得成立的最小正整数,则m 在以下哪个区间?

解:

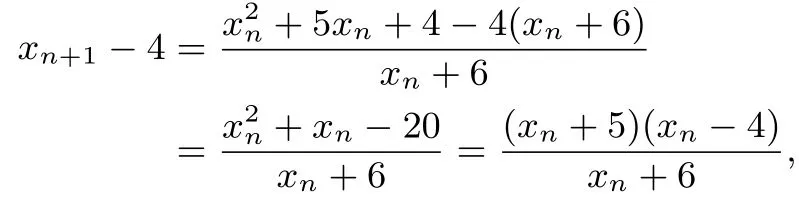
由于x0>4,可得xn+1>4,∀n ∈N;又

可得数列{xn}是单调下降的,则4 < xn5,进一步可得

25.How many sequences of 0s and 1s of length 19 are there that begin with a 0,end with a 0,contain no two consecutive 0s,and contain no three consecutive 1s?

(A) 55 (B) 60 (C) 65 (D) 70 (E) 75

译文: 有多少个长度为19 的只含0 和1 的序列: 以0 开头,以0 结尾,不包含两个连续的0,也不包含三个连续的1?

解: 0 后面只能接1 或11, 记01 为A, 011 为B, 原问题就相当于将一些A 和B 排列在长度为18 的序列上, 可能出现(1) 6 个B: 只有1 种排列; (2) 4 个B, 3 个A: 共有种排列; (3) 2 个B, 6 个A: 共有种排列;(4)9 个A: 只有1 种排列.因此,符合条件的序列共有1+35+28+1=65 个,故(C)正确.