立足整体换元 回归基本流程

广东省广东北江中学(512026) 陈继平

一、以小见大,比值换元为一元问题

问题1已知实数x,y 满足x2+(y−2)2=1, 则的取值范围是( )

A.B.[1,2] C.(0,2] D.

笔者所在学校的学生数学学习的整体水平还不错,但给出这个题目后大部分同学还是很难想到怎么处理,更别提用最简单的几何意义来处理了,但我们立足于通法,发现过程本质是比值换元为一元函数问题,把取值范围问题转化成函数的值域问题则自然得多.

由于x2+(y−2)2=1 表示的圆恒在的上方, 结合线性规划知识可知于是ω =设则设结合图形,由线性规划知识易知或于是t2 或t−4.当t2 时,则当t−4时,< 0,1f(t) < 3,则特别的x=0,y=1 或3,则综上:1ω2,故选B

二、由此及彼,比值换元处理综合问题

从上面一个选择题以小见大,发现比值换元后转化成一元函数是我们很熟悉的问题,也避免多元变量对我们的干扰,起到化繁为简的目的,下面利用上面的处理策略,由此及彼的解决函数不等式的综合问题,以求立足基本通法,更加进一步的理解换元过程的本质.

问题2设函数f(x)=x2,g(x)=a ln x+bx(a > 0)．设G(x)=f(x)+2−g(x)有两个零点x1,x2,且x1,x0,x2成等差数列,试探究G′(x0)值的符号．

解析G′(x0)的符号为正.理由如下:

因为G(x)=x2+2−a ln x−bx 有两个零点x1,x2, 则有两式相减得−b(x2−x1)=0,即x2+x1−b=于是

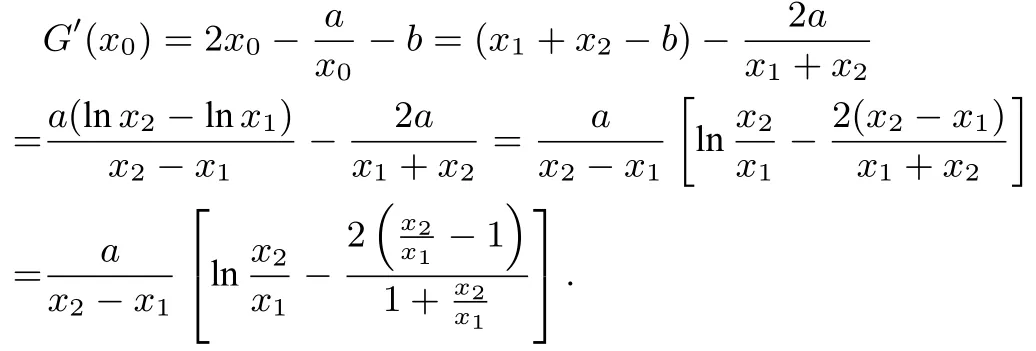
①当01,且G′(x0)=设则则u(t) =在(1,+∞) 上为增函数．而u(1)=0, 所以u(t)>0,即ln又因为a>0,x2−x1>0,所以G′(x0)>0.

②当00.

综上所述: G′(x0)的符号为正.

由以上分析总结不难发现,对于二元变量x1,x2的处理是该问题的关键,通过两边提取x2−x1,经过换元将G′(x0)的符号的判定问题转化成一元函数u(t)的符号的判定问题.

问题3已知函数f(x)=2 ln x−x2(x > 0),如果函数g(x)=f(x)−ax 的图像与x 轴交于两点A(x1,0),B(x2,0),且0 < x1< x2,求证: g′(px1+qx2) < 0(其中正常数p,q满足p+q =1,q >p).

解析因为f(x)−ax=0 有两个实根x1,x2, 所以两式相减得2(ln x1−ln x2)−所以因为于是

因为p < q, 所以2p < p+q=1, 并且0 < x1< x2,所 以(2p−1)(x2−x1) < 0.要 证: g′(px1+qx2) <0, 只 需 证:只需证:即

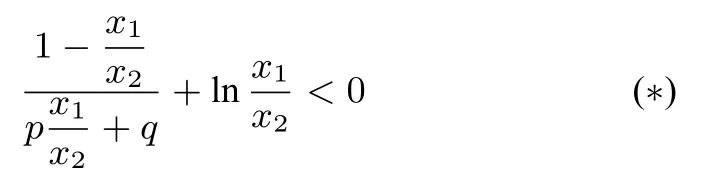
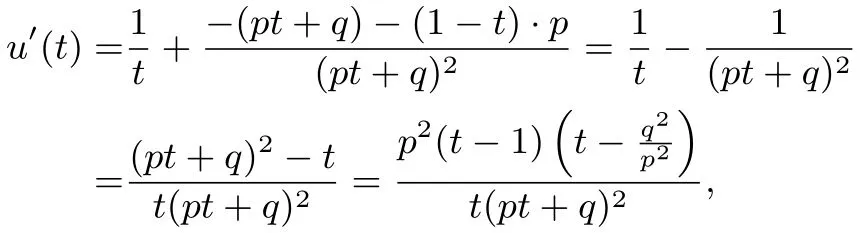
三、触类旁通,差值换元为一元问题

题目4已知函数

(1) 若函数f(x) 的图象在x=0 处的切线方程为y =2x+b,求a,b 的值;

(2)若函数f(x)在R 上是增函数,求实数a 的取值范围;

解析(1)(2)略.

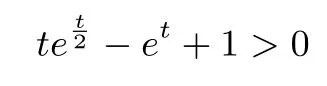
从以上问题可以看出一个共同点, 不论问题怎么变化,都使用了整体打包x1−x2进行换元为t 的方式,追根溯源其本质是一种消元的转化意识.

四、类比推广,和值或积值换元为一元问题

事实上立足于这种思想, 我们能找到或编制有关于x1+x2和x1x2这类和值或积值换元吗? 答案是太多太多.尤其在解几中会经常碰到,例如: 过椭圆2x2+y2=2 的焦点的直线交椭圆A,B 两点,求△AOB 面积的最大值.简析:设过焦点(0,1)的直线方程为y=kx+1 与2x2+y2=2联立,消去y, 得(2+k2)x2+2kx−1=0,其中两根x1,x2为A,B 横坐标.将△AOB 看作△AOF 与△BOF 组合而成 ,|OF|是公共边 ,它们在公共边上的高为|x1−x2|.故

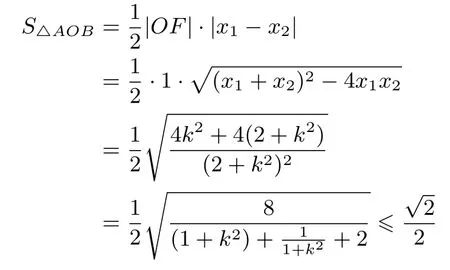
(当k =0 时取等√号),即当直线为y =1 时, 得到△AOB 的面积最大值为不难发现解几中利用韦达定理整体打包x1+x2和x1x2的本质都是一类和值或积值换元.

通过以上诸如此类问题的思考,我们有理由相信立足于基本通法,理解过程是换元的本质,回归到基本方法这个流程上来,就不会掉入就题论题的陷阱.这样即帮助学生达到做一题,通一类,会一片的效果,同时也对教师的高效课堂提供了一种有效途径.