对一个条件概率问题的再辨析以及思考
广东省珠海市斗门区第一中学(519000) 李 凯 郑 玲
在《中学数学研究》(华南师范大学版上半月) 2018年第六期P21-22 中刊登了文章《一个条件概率问题的辨析》(后面简称文[1]).文中讨论了计算一道条件概率题的常见三种方法: 缩小概率空间法, 条件概率公式, 利用全概率公式.并且对它们所计算结果不一样进行了探究.文中指出的“计算结果不一样”引起了笔者的思考.笔者经过再探究发现, 其实三种方法都可以用来计算条件概率, 文中的“计算结果不一样”都源于一个公式用错.即文[1] 中用到的公式: 若A1,A2,B 表示三个事件, 且A1∩A2=∅, 则P(B|A1∪A2)=P(B|A1)+P(B|A2).这里将这个用错的公式记为公式1.
一、公式1 是否成立的思考及正确形式
当A1∩A2=∅时,即A1,A2互斥,故BA1,BA2也互斥,故P(A1∪A2)=P(A1)+P(A2),P((BA1)∪(BA2))=P(BA1)+P(BA2),根据条件概率的公式:
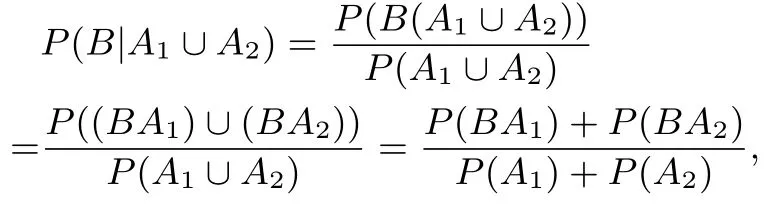
而
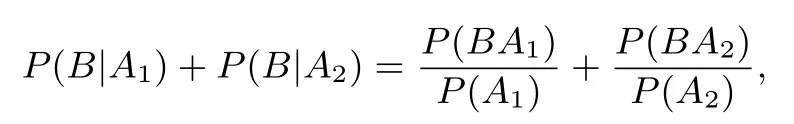
显然

并且易知一般情况下等号不成立.故公式1 一般情况下是不成立的.
如下图可通过韦恩图非常容易看到它们的区别与关系:
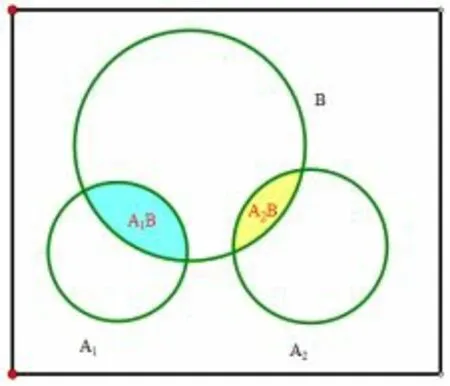
图1
受韦恩图以及上面的推导的启发,可对公式1 修改一下也能得到一个正确的结论: 若A1,A2,B 表示三个事件, 且A1∩A2=∅,则P(B|A1∪A2)=P(A1|A1∪A2)P(B|A1)+P(A2|A1∪A2)P(B|A2).这里记为公式2.观察公式2 的形式,它与全概率公式

在人教A 版选修2-3 教材[2]P60 中有一个与条件概率性质有关的习题: 设事件A,B,C 满足P(A)>0,B 与C 互斥,证明P(B ∪C|A)=P(B|A)+P(C|A).这个性质是正确的,不应与用错的公式1 混淆.
二、重解文[1]中的题目
先分析文[1]中例1 的变式题,题目如下: 掷骰子两次,求在第一次掷得的点数为1 或2 的条件(记为A)下,两次掷得的点数之和为5(记为B)的概率.
解法1(缩小空间法)
第一次掷得的点数为1 或2 的条件下, 所有的试验结果可记为(x,y), x ∈{1,2}, y ∈{1,2,3,4,5,6} 共12 个, B 事件满足的基本事件有(1,4), (2,3) 两个, 故
解法2(利用条件概率的定义)
解法3(利用公式2)
把第一次掷得点数1,2 分别记为A1,A2,显然A1∩A2=∅,这样
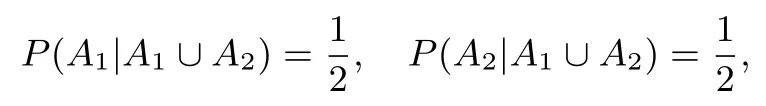
而

故

分析三种解法答案均为在文[1]中计算为是在缩小空间法中把概率空间弄错了;事实上,概率空间应该是两次的试验结果.在第一只试验中虽然结果是1 或2,但它们只能发生一个,这样在事件A 发生的情况下,事件B 并不能等价于第二次的结果为4,3.也可以从这种角度来理解: 当第二次的结果为4 时,只有的概率发生了B,同样当第二次的结果为3 时,也只有的概率发生了B.这也即是对公式2 的实际意义的理解.
同样的道理,在文[1]中一开始提出的测试题中解法二应该是正确的,正确答案应该是而文[1]解法一与解法三是错误的,通过与上面例1 的变式题类似的分析与改正可得正确的解法.
三、辨析之后的思考
非常赞同文[1]中的观点,平时在命条件概率题目时一定要严把语言关,避免产生同一种语言表述会有P(AB)与P(B|A)两种不同的理解.事实上,上述三种解题方法正好是计算条件概率的三种典型方法: 定义法,缩小样本空间法,利用概率的运算法则与事件之间的关系间接计算.在高考题中,计算条件概率在高考中并不算一个非常热门的考查方向,但由于教材中对这一块内容要求不高,师生普通重视不够.当在考试中涉及时,学生往往失分较多,能灵活的运用三种方法来计算,方可以不变应万变.另外,在某些概率的计算中,直接用古典概型的模型来计算不易处理,而反过来通过逆用条件概率公式来计算概率,非常容易理解,我们也要重视.下面就这两方面做一些思考与探究.
(一) 例析条件概率的三种典型计算方法
1 直接利用定义计算条件概率
例1(2014年全国二卷理科第5 题).某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是( ).
A.0.8 B.0.75 C.0.6 D.0.45
解设某天的空气质量为优良为事件A,随后一天的空气质量为优良为事件B,由已知P(A)=0.75,P(AB)=0.6,根据条件概率的定义,选A.
例2甲、乙两人独立地对同一目标各射击一次,其命中率分别为0.5,0.8,现已知目标被击中,则甲击中目标的概率是( ).
A.0.8 B.0.9 C.D.
解根据题意, 记甲击中目标为事件A, 乙击中目标为事件B,目标被击中为事件C,则P(C)=1−P(¯B)P(¯A)=1−(1−0.8)(1−0.5)=0.9;又AC =A,则根据定义,甲击中目标的概率为故答案为D.
2 缩小样本空间来计算条件概率
例32018年6 月18 日,是我国的传统节日“端午节”.这天,小明的妈妈煮了5 个粽子,其中两个腊肉馅,三个豆沙馅.小明随机抽取出两个粽子,若已知小明取到的两个粽子为同一种馅,则这两个粽子都为腊肉馅的概率为( ).
解记小明取到的两个粽子为同一种馅为事件A, 两个粽子都为腊肉馅为事件B, 则A 包含的基本事件的个数为而B 包含的基本事件的个数为1, 故选A.
例4从装有大小形状完全相同的3 个白球和7 个红球的口袋内依次不放回地取出两个球,每次取一个球,在第一次取出的球是白球的条件下,第二次取出的球是红球的概率为( ).
A.B.C.D.
解在第一次取出的球是白球的条件下,第二次口袋内的球一定是2 个白球和7 个红球,易得第二次取出的球是红球的概率为选D.
3 利用概率的运算性质间接计算
例5设某公路上行驶的货车和客车的比例为2 : 1,货车在中途停车修车的概率为0.02,客车在中途停车修车的概率为0.01,今有一辆汽车停车修理,求该汽车是货车的概率.
解记该车为货车为事件A1,该车为客车为事件A2,汽车停车修理为事件B,则而

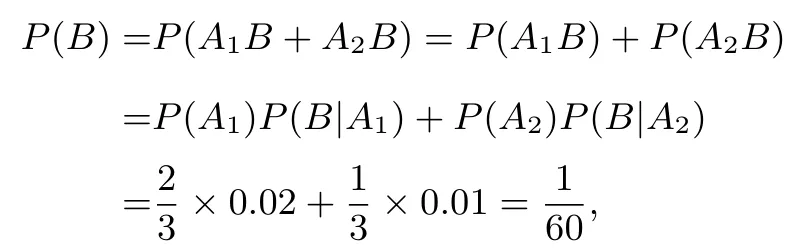
例6某医院用一仪器对某种疾病进行初步诊断,已知这种仪器对患病者的正确诊断概率有0.9;对没患病者的正确诊断率有0.8.已知这种疾病在人群中的患病的比例为0.1,若某人去医院就诊,在医院通过这种仪器初诊给出的诊断结论是已患病的条件下,求此人真正患这种病的概率.
解记仪器初诊给出的诊断结论是已患病为事件A,此人真正患这种病为事件B,则而事件A包含两种情况: 即就诊者真正患病而被诊断患病和就诊者没患病而被诊断患病,这样A=AB ∪且
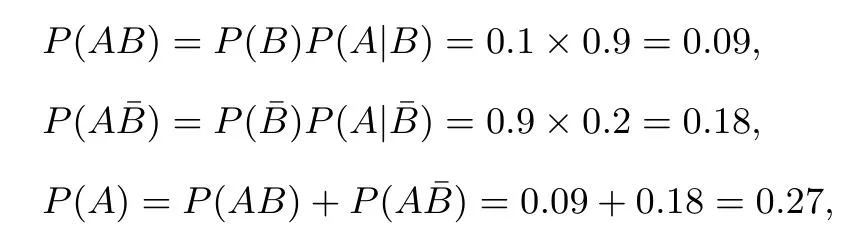
注: 此题的计算具有一定的实际意义,在医院里不仅需要对生病的人要正确的诊断和治疗,对一些疑似生病的健康人也要正确诊断, 在本题中因为对健康人的误诊率比较高,导致最后对这个就诊者的正确诊断率只有
对于以上三种方法, 应付高中阶段的常规考试, 方法1和方法2 足以;对于方法3 主要是借鉴了贝叶斯公式和全概率公式的思想,可以很好的扩展学生的知识面.
(二) 逆用条件概率公式来计算概率
例7(2015年高考福建卷理科第16 题)某银行规定,一张银行卡若在一天内出现3 次密码尝试错误,该银行卡将被锁定,小王到银行取钱时,发现自己忘记了银行卡的密码,但是可以确定该银行卡的正确密码是他常用的6 个密码之一,小王决定从中不重复地随机选择1 个进行尝试.若密码正确,则结束尝试;否则继续尝试,直至该银行卡被锁定.
(I) 求当天小王的该银行卡被锁定的概率;(II) 略.
解(I) 设“当天小王的该银行卡被锁定”的事件为A, 记小王第i (i=1,2,3) 次按的是错误密码为Ai, 则A=A1A2A3,显然对于计算P(A2|A1),相当于在第一次按的错误密码的条件下,第二次又在5 个密码中又按了错误的密码,故同理
故
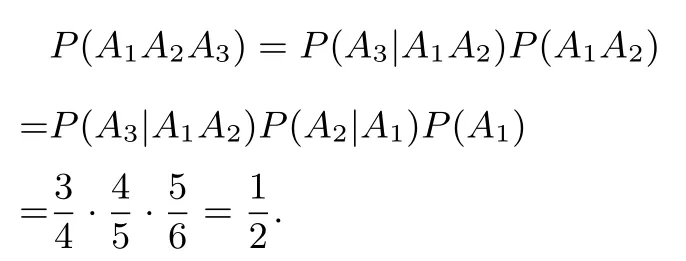
注: 在教学中发现不少学生都用古典概率模型来解题,解题思路如下: 记六个密码分别为t,f1,f2,f3,f4,f5(其中t为正确密码),用(a,b,c)来表示前三次试验的结果.在前三次尝试中,总的基本事件的个数为而银行卡被锁定即前三次按的均是错误密码,则基本事件的个数为故银行卡被锁定的概率
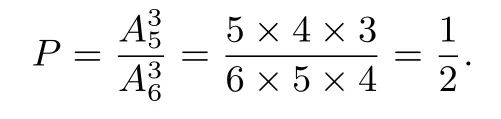
这样求解虽然最终计算得结果正确,但是原理与题意不相符,比如(t,f1,f2)在实际中根本不会出现,因为当第一次就密码正确后,就不会在尝试第二次,第三次,所以此题并不适合用古典概型来解.反而此题容易求条件概率,通过逆用条件概率公式来求概率更容易理解.
例8(武汉市2018 届高中毕业生四月调研测试理科数学试题).一张储蓄卡的密码共有6 位数字,每位数字都可以从0-9 中任选一个,某人在银行自动提款机上取钱时,忘记了密码最后一位数字,如果任意按最后一位数字,不超过2 次就按对的概率为( ).
A.B.C.D.
解记“第i 次按对密码”用事件Ai表示,记“不超过2次就按对”用事件A 来表示,则A 可表示为A=A1∪显然
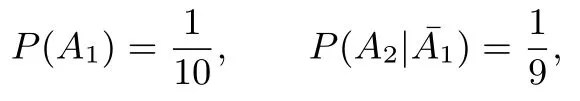
这样
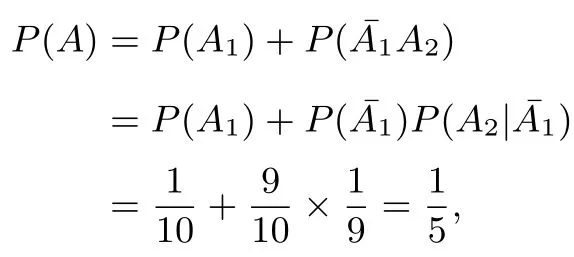
选C.

