一类二元函数最值问题的求解

陕西省西安交通大学附属中学(710054) 石鸿鹏

陕西省西安交通大学附属中学分校(710048) 李亚玲

二元函数在近几年的高考中经常出现,尤其是二元函数的最值问题,能够充分体现化归转化、数形结合等重要思想.本文将探讨以下这类二元函数最值问题:

已知x>0,y >0,若ax+by+xy+c=0(a,b,c 均为常数),求x+y 的最小值.

一、几何意义

理清问题的几何背景与几何意义,能够从根本上把握问题的核心,对问题的解决大有裨益.

对于ax+by+xy+c=0 可以做如下变形:

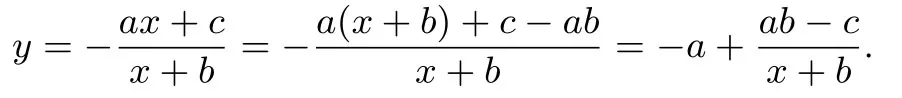
图1

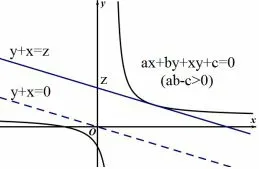
图2

二、实例探究

以下通过具体实例来探究此类问题的各种解法及其本质.

例1设x>0,y >0,且2x+8y =xy,求x+y 的最小值.

(一) 基于基本不等式的变形与配凑

解法一注意到条件与结论的特殊关系,可将条件巧妙变形为从而有x+y=(x+y)再根据基本不等式可以求解.

解由于x > 0,y > 0, 则2x+8y=xy 可以形变为:所以x+y =(x+y)由均值等式得:当且仅当时,取等号,与2x+8y =xy 联立得: x=12,y =6,所以,当x=12,y =6 时,(x+y)min=18.

总结评注当题目的条件为ax+by+xy=0 时,可以变形为再根据等式两边乘1 不变的性质知:x+y=(x+y)当a < 0,b < 0 时,用基本不等式可以求得x+y 的最小值;当a > 0,b > 0 时,用基本不等式可以求得x+y 的最大值;当a、b 异号时则不能用基本不等式.因此,这种方法只适用于条件可以变形为且c、d 同为正数情况下求x+y 的最小值的情况，属于特殊方法，对本文所探讨的最值问题没有普适性.

解法二由基本不等式知,若ab=s(积为定值),当且仅当因此,可以尝试把已知条件变形为关于x、y 的因式之积等于常数,再根据上述性质求最值.

解由2x+8y=xy 得: (y−2)x=8y, 又x >0,y > 0, 则y−2 > 0, 又2x+8y=xy 可以配凑为:(x−8)(y−2)=16,则x−8 > 0,所以由均值不等式,得:x+y =(x−8)+(y−2)+10+10=18,当且仅当x−8=y−2 时取等号,与2x+8y =xy 联立得:x=12,y =6,所以,当x=12,y =6 时,(x+y)min=18.

总结评注由于ax+by+xy+c=0 可以变形为:(x+b)(y+a)=ab−c, 又由几何意义部分的讨论知ab−c > 0, 则x+y=(x+b)+(y+a)−a−b所以当且仅当x+b=y +a 时,将x+b=y+a 与ax+by+xy+c=0 联立不难求出使x+y取得最小值时x、y 的值.因此,这个方法是解决此类最值问题的通法.

解法三由于问题是求x+y 的最小值,因此可以将已知条件变形为一边为x+y 的等式,然后根据不等式的性质求解.

解2x+8y=xy 可以配凑为: 2(x+y)=(x−6)y当且仅当x−6=y 时取等号,与2x+8y =xy联立得: x=12,y =6,设x+y =t,由上法知: x>8,y >2,则t>10,所以即t2−20t+360(t>10),解得: t18,即当x=12,y =6 得: tmin=(x+y)min =18.

总结评注由于ax+by+xy+c=0 可以变形为:a(x+y)=−c−(b−a+x)y,则根据不等式得: a(x+y)=−c−(b−a+x)y−c−令t=x+y,则at−c此是关于t 的一元二次不等式, 是很容易求解的.这种方法需要注意的是t的范围,需要如例题中对已知条件适当变形判断出一个t 的范围.显然,此法是解决此类最值问题的通法.

(二) 基于方程思想的解法

解法四(代入消元法)已知条件是关于x、y 的等式,可以把一个变量用另外一个变量表示出来,通过带入消元法使二元最值问题变为一元最值问题,再通过适当的方法求解一元最值.

解由2x+8y=xy, 得y(x−8)=2x, 因为x > 0,y > 0, 所 以所 以x+y =当且仅当即x=12 时,等号成立所以,当x=12 时,x+y 取得最小值18.

总结评注关于两个变量间存在等式关系的最值问题,通过消元法将二元最值问题化为一元最值问题,这是最基本的处理方法,是此类最值问题的通法.但要特别注意消元以后剩余元的取值范围.

解法五(判别式法) 该类问题的几何意义是在曲线ax+by+xy+c=0 与直线z=x+y 有公共点时,直线z=x+y 在y 轴上的截距的最小值.而两个函数的公共点的一般求法是把两个函数的解析式联立,所成方程的解即能确定公共点.

解设x+y=t (t > 10), 则x=t−y, 所以2(t−y)+8y=y(t−y), 即y2+(6−t)y+2t=0, 所以∆= (6−t)2−8t=t2−20t+360(t > 10), 解得:t18,所以(x+y)min=18.

总结评注设x+y=t, 即x=t−y, 将其带入ax+by+xy+c=0,得y2+(a−b−t)y−at−c=0.这是关于y 的一元二次方程,t 为参数,两个函数有公共点,即此方程有实数解,则∆= (a−b−t)2+4(at+c)0,求解这个关于t 的一元二次不等式,求解这个不等式,求出t 的范围,即可求出(x+y)min.此法也是求解此类最值问题的通法.

三、小结

对于本文所探讨的这类最值问题,通过对几何意义的刻画和实例的探究,我们从不同的切入点总结出了解决这类最值问题的4 种通法,对于1 种只适用于个别题目的特殊方法进行了说明.