从一道高考试题探究函数性质的联系*

安徽省砀山中学 (235300)

盖传敏

众所周知，函数的奇偶性、周期性及图像的对称性在函数中占有极其重要的地位，与之相关的问题在近几年高考试卷及模拟试卷中频繁出现，那么这“三性”之间有何联系呢？本文结合一道高考题探讨了“三性”之间的联系，以供参考.

1.试题呈现

(2018课标2，11)已知f(x)是定义域为(-∞,+∞)的奇函数，满足f(1-x)=f(1+x).若f(1)=2，则f(1)+f(2)+f(3)+…+f(50)=( ).

A.-50B.0C.2D.50

解析:由f(1-x)=f(1+x)可得，函数f(x)关于直线x=1对称，即f(-x)=f(2+x)(1)，又由f(x)是定义域为(-∞,+∞)的奇函数，可得f(0)=0,f(-x)=-f(x)(2).联立(1)，(2)两式可得f(x+2)=-f(x)，即f(x+4)=-f(x+2)=f(x)，所以函数f(x)的最小正周期为4，又因为f(1)=2，f(2)=f(0)=0，f(3)=f(-1)=-2，f(4)=f(0)=0，所以f(1)+f(2)+f(3)+…+f(50)=12×0+f(49)+f(50)=f(1)+f(2)=2.

2.探究拓展

性质1 若函数f(x)为奇函数且关于直线x=a(a≠0)对称，则f(x)是T=4a的周期函数.

证明:由函数f(x)关于直线x=a对称，可得f(-x)=f(2a+x)(1),又由函数f(x)为奇函数，可得f(-x)=-f(x)(2).联立(1)，(2)两式可得f(x)=-f(2a+x)，即f(x)是T=4a的周期函数.

性质2 若函数f(x)为偶函数且关于直线x=a(a≠0)对称，则f(x)是T=2a的周期函数.

证明:由函数f(x)关于直线x=a对称，可得f(-x)=f(2a+x)(1),又由函数f(x)为偶函数，可得f(-x)=f(x)(2).联立(1)，(2)两式可得f(x)=f(2a+x)，即f(x)是T=2a的周期函数.

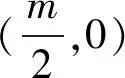
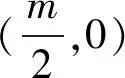
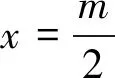
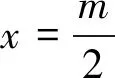
性质5 若函数f(x)关于直线x=m(m≠0)对称且是T=m的周期函数，则f(x)是偶函数.

证明:由函数f(x)关于x=m(m≠0)对称，可得f(-x)=f(2m+x)(1)，又因为f(x)是T=m的周期函数，可得f(x)=f(2m+x)(2).联立(1)，(2)两式可得f(x)=f(-x)，即f(x)是偶函数.

性质6 若函数f(x)关于点(m,0)(m≠0)对称且是T=m的周期函数，则f(x)是奇函数.

证明:由函数f(x)关于点(m,0)(m≠0)对称，可得f(-x)=-f(2m+x)(1)，又因为f(x)是T=m的周期函数，可得f(x)=f(2m+x)(2).

联立(1)，(2)两式可得f(-x)=-f(x)，即f(x)是奇函数.

3.性质应用

(2014大纲全国，12)奇函数f(x)的定义域为R，若f(x+2)为偶函数，且f(1)=1，则f(8)+f(9)=( ).

A.-2B.-1C.0D.1

解析:由f(x+2)为偶函数可得，函数f(x)的图像关于直线x=2对称，又因为函数f(x)为奇函数，由性质1可得函数f(x)是以8为周期的函数，所以f(8)+f(9)=f(0)+f(1)=1.

4.结束语

以上可以看出，函数的奇偶性、周期性、对称性三者之间相互联系，在实际教学中若能从整体上把握这些性质，可以帮助学生开阔视野，对于提高学生的数学抽象、逻辑推理等数学核心素养都有很大帮助.