《一次函数的图象与性质》课例设计

陈 姗

(广东省珠海市第十中学 519000)

一、背景介绍

本课是教研公开课，课例进行了积极设计，意在学生在教师指导下能顺利落实学习目标，理解并掌握课本的知识点，培养学生的动手操作能力、合作探究能力.

二、备课过程

1.地位作用

一次函数是各类函数中最简单的一种，反映了函数特点及函数的思维方式、研究方法和应用模式，因此学好一次函数是学好其他函数的基础.

2.课标要求

学生能画出一次函数图象，根据图象和表达式y=kx+b(k≠0)探索并理解k>0和k<0时图象的变化情况.

3.教材理解

补充：当直线y1=k1x+b1与y2=k2x+b2平行时，则k1=k2且b1≠b2，反之亦成立；常数项b对图象的影响.

4.中考分析

利用函数图象求系数取值范围，或根据系数判断函数图象位置；运用一次函数知识解决实际问题如利润最大；利用方程(组)确定函数图象特殊点(公共点)坐标，利用一次函数图象求一元一次不等式(组)解集等；一次函数与其他代数、几何知识综合应用.

5.学情分析

八下学生思维活跃趋成熟，但好奇心不减，具备抽象、猜想、归纳、证明、总结等能力，且学生已有研究函数图象与性质的经验和方法.

三、教学设计

学习目标:(1)会用两点法画一次函数的图象；(2)能从图象角度理解正比例函数与一次函数的关系；(3)能根据一次函数的图象和表达式y=kx+b(k≠0)，理解k、b对函数图象的影响.

重、难点：k、b的值与图象位置的关系.

(一)复习与预习

复习：1.画函数图象的步骤；2.正比例函数与一次函数的关系；3.正比例函数y=kx(k≠0)的图象和性质.预习：展示学生所画函数y=x、y=x+2、y=x-2的图象.

(二)探究新知

活动一：探究一次函数与正比例函数的联系观察函数y=x、y=x+2、y=x-2的图象.

总结：

1.形状：一次函数y=kx+b的图象是一条____线

2.平移规律：一次函数y=kx+b的图象可以由直线y=kx平移____个单位长度得到：当b>0时，它是由y=kx向____平移____个单位长度得到；当b<0时，它是由y=kx向____平移____个单位长度得到.

3.一次函数图象画法：两点法、平移法.

例1在同一个直角坐标系中，把直线y=-2x向____平移____个单位就得到y=-2x+3的图象；若向____平移____个单位就得到y=-2x-5的图象.

活动二：探究一次函数中k对图象的影响.

继续观察图象：

1.三条直线的倾斜度____，三个函数解析式中k值____，它们的位置关系____;

2.当k>0时，函数的图象从左到右____，y随x的增大而____； 当k<0时，函数的图象从左到右____，y随x的增大而____.

例2 已知直线y=(k-1)x+2，当k=____，该直线与直线y=2x-5平行；当k____，y随x的增大而增大.

例3 已知点(-1，a)、(2，b)在直线y=-3x+8 上，则a，b的大小关系是____.

活动三：探究一次函数中b对图象的影响.

在同一坐标系中用两点法画出以下2个函数图象

x01y=2x-1

x01y=-x+1

(1)y=2x-1 (2)y=-x+1

一次函数常数项b对图象的影响

图象与y轴的交点坐标是____，当b>0时，图象交y轴____半轴；

当b=0时，图象经过____点;

当b<0时，图象交y轴____半轴.

练习：1.直线y=-2x+4从左往右____，y随x增大而____，与y轴交点坐标____，与x轴交点坐标____.

直线y=-2x+m-3与y轴的负半轴相交，则m的取值范围____.

总结：一次函数y=kx+b图象与性质

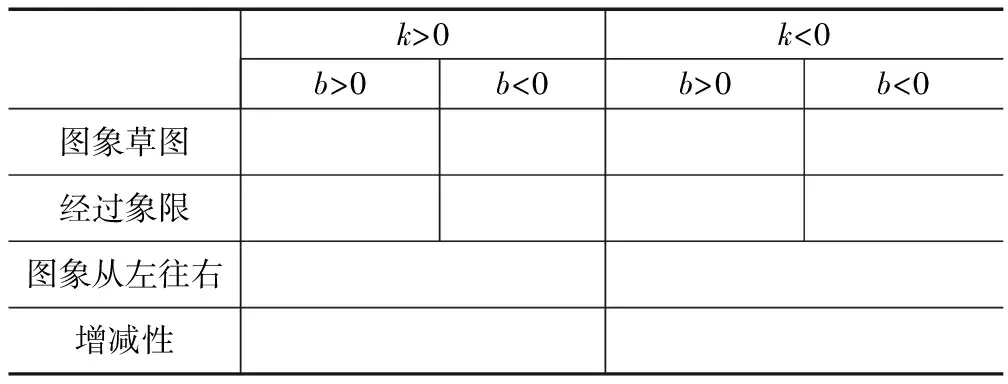
k>0k<0b>0b<0b>0b<0图象草图经过象限图象从左往右增减性

练习：已知直线y=(1-3k)x+2k+1.

(1)当k为何值时，该直线经过第二、三、四象限？

(2)当k为何值时，该直线与直线y=-2x+2平行？

(3)当k为何值时，该直线与直线y=2x+5在O轴交于同一点？

四、反思

初学一次函数，学生停留在感性认识多、理性认识少，对简单问题(直接应用图象特征判断问题特征等)往往能根据课堂所学的知识，再加上参考书本知识，例题练习模仿解决，通常看不出一次函数的理解程度，但随着问题复杂化，学生对解析式与图象的内在联系运用呈现薄弱之势，需后续多练多探多问，总结经验.

不足之处：缺乏现代信息技术的运用，如几何画板、超级画板的使用，能帮助学生更好地理解一次函数的图象与性质，更深入体会数形结合思想.