分类讨论在初中数学解题中的应用

陈 磊

(江苏省镇江市宝堰中学 212125)

一、分类讨论的概念

在研究某一问题时，不能用统一的方法进行研究，这时需要采用一个标准，将问题进行分类别研究，得出每一种类别的结果，最后综合每一种类别的结果给出整个问题的结果，这就是分类讨论的思想方法．简而言之，就是先通过对研究对象进行分类，再分别研究，最后综合解决问题．

二、分类讨论的原则

初中阶段采用分类讨论应遵循以下原则：

(1)一致性原则：每一次分类的标准必须是一致的．如对三角形进行分类，必须采用一致的标准，按边分为等腰三角形、不等边三角形；按角分为锐角三角形、直角三角形、钝角三角形．

(2)不重复原则：所有类别之间必须是互斥的．如折线上的动点问题，端点A归属于第一种情况，就不能再重复归属于第二种情况．

(3)不遗漏原则：分类必须包括所有类别，不出现遗漏．如整数分为正整数、负整数，还有零，零就不能被遗漏．

(4)层次性原则：分类必须逐级进行，不能越级．如实数的分类上，分为有理数和无理数，有理数分为整数和分数，整数分为正整数、零、负整数．层次分明，不同标准的不同层次的分类不能混淆．

三、分类讨论的步骤

在解题的过程中，用分类讨论思想方法解决初中数学问题时，不仅要遵循上述的四个原则，也要保证在解题过程中的科学、严谨、全面，还要依据分类讨论的具体步骤操作．

1.分析问题，明确分类对象

一般而言，运用分类讨论思想方法解决问题时，要先对问题进行分析，发现问题中有变幻不定的影响因素或者有问题不便于统一处理，确实需要采用分类讨论的方法进行解决，并明确将对谁进行分类．

2.回顾知识，寻找分类标准

明确分类对象后，需要回顾和对象有关的知识网络，找出破坏统一处理的要素或原因，寻找一个标准，能区分所有的情形，能把复杂的不确定的“动态型”问题分解为多个便于具体操作的子问题来解决．

3.分类讨论，处理各类情形

有了统一的分类标准，我们就针对该问题进行分类，针对每一类情况，实施该情况内的解题策略，且最后结论也该是这一类情况内.这里，我们也有一个原则，那就是先解决简单的情况，然后，尽力设法寻找其他情况与该情况的异同点，再各个击破．如分类不能一次完成，再进行上述重复过程．

4.归纳综合，揭示总体结论

各种类型的情况研究完并不意味着整个问题的解决，需要将所有情况的结论进行归纳综合，得出最终结论．

这四个步骤概括的说无非就是一个从确定分类对象、寻找分类标准到分类解决问题，再到综合归纳总结出结果的过程．

四、分类讨论在初中数学解题中的应用

根据以上的分析，笔者以近几年中考题为例，阐述分类讨论在中考解题中的应用．

1.根据概念进行分类讨论

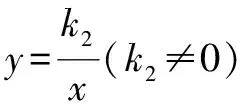
2.根据运算进行分类讨论

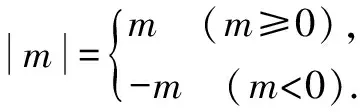
注意m=0的情况，遵循不重复性的原则．最后将结论汇总得出需要解决问题的综合结论：m=-1或m=3．

3.根据函数性质进行分类讨论

例3 若点A(m，n)在直线y=kx(k≠0) 上，当-1≤m≤1时，-1≤n≤1，则这条直线的解析式为____．

分析该题首先要对一次函数图象与性质有所理解，寻找分类对象，那就是比例系数k，回顾知识点：当k>0时，y随x的增大而增大；当k>0时，y随x的增大而减小．对k分两种情况进行讨论研究：① 当k> 0时，m=-1时，n=-1；m=1时，n=1，此时，y=x.② 当k<0时，m=-1时，n=1；m=1时，n=-1，此时，y=-x.最后将结论汇总得出需要解决问题的综合结论：这条直线的解析式为y=x或y=-x．

4.根据时间进行分类讨论

例4 已知：如图所示，在平面直角坐标系xOy中，四边形OABC是矩形，OA=4，OC=3，动点P从点C出发，沿射线CB方向以每秒2个单位长度的速度运动；同时，动点Q从点O出发，沿x轴正半轴方向以每秒1个单位长度的速度运动．设点P、点Q的运动时间为t(s)．连接CQ，当点P，Q在运动过程中，记△CQP与矩形OABC重叠部分的面积为S，求S与t的函数关系式．

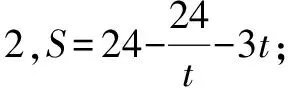
分类讨论思想的应用非常广泛，涉及到的知识点较多，解决关键在于弄清引起分类的原因，明确要分类讨论的对象与标准，分不同情况各个击破，再将各个结论归纳总结，综合得出最后正确结论，这其实就是一个总—分—总的过程．分类讨论思想是一类重要的数学思想，教师一方面引导学生理解其分类精髓，学会运用分类思想解题，另一方面也要不断培养学生的数学思维能力，对学生学习其它数学思想会产生积极作用．