特殊化策略在初中数学解题中的应用

王朝梅

(安徽省合肥市50中学南校 230000)

目前，初中数学问题在解答过程中普遍具有特殊性，故而教师在进行数学习题解答的过程中，需要加强对于特殊化策略的运用.本文基于此，着重论述特殊化策略在数学习题中的运用，希望由此实现数学教学质量以及效率的提升，促进各项教学效果的取得.

一、特殊化策略运用与思维严谨培养

我国中学阶段开设数学科目的主要原因，在于培养学生的思维能力.一般而言，学生在进行数学习题解答的过程中需要进一步保障答题的严谨性以及周密性.数学习题在解答分析作业时普遍具有思维严谨性，且需要遵循一定的逻辑规律.基于此，教师引导学生明确解题思路，并巧借特殊化方法，从特殊最佳情形入手探究和分析数学问题，实现学生解题思路的开拓，并进一步培养学的逻辑思维能力.

例1 “如图1所示，在Rt△ABC中，∠ACB=90°,CD⊥AB,垂足为D，点E在AC上，BE交CD于点G，EF⊥BE交AB于点F，若AC=mBC，CE=nEA(m，n为实数)，请探究线段EF与EG的数量关系.”

对于初中的学生而言，这一道题目具有一定的难度，学生如果借助一般的几何分析方法进行解答时，往往会陷入思维僵局中，但是学生如果采取特殊化的策略进行解答，其往往能够实现问题的突破，促进问题解答效率以及质量的提升.

二、特殊化方法与思维批判性培养

所谓的数学思维批判性，指的是学生在数学问题解答时能够具备独立思考的能力，同时能够科学地进行数学问题的分析以及解答，并对材料中的论证论据提出质疑.一般而言，特殊化方法的合理化运用，能够进一步地培养学生判断疑问的能力，从而进一步引导学生对于各类论据特殊情况的分析.目前，教师在进行数学题解答分析教学时，可以巧妙地利用各类特殊化方法，引导学生对于各特殊情况的分析以及验证，从而确保其能够对自己的解题不足之处进行总结、认识，实现了自身的完善发展，可以在最大程度上带动了其解题思维以及明辨是非能力的增长.

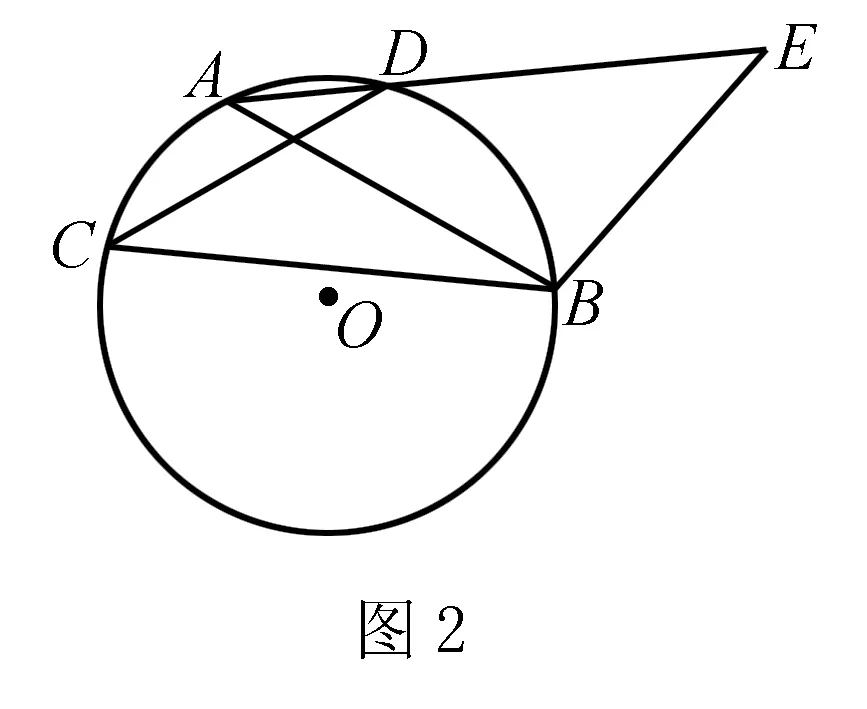
以数学题“有一组对边和一组对角相等的四边形是平行四边形是否是真命题” 为例进行相关的分析.如图2所示：在⊙O中作出两条相交的等弦AB、CD，并将AD、BC进行连接，延长AD至E点，并使BE=AB.这一作图之后能够得到等腰三角形△ABE，而四边形CDEB这就符合上述的命题假设.在这一命题假设的影响下，我们可以得知∠C=∠E，而且线段CD与线段BE的长度相等.但事实上，如果四边形CDBE并非平行四边形，则上述的命题为假命题.

三、特殊化策略与思维灵活性培养

所谓的灵活性思维，指的是学生在数学问题分析以及解决的过程中，能够进一步打破传统的思维模式，并借助不同的视角、层面进行问题的思考以及发掘，从而明确问题的解决方法.目前，我国的中学生在数学学习的过程中，普遍依赖教师，进而导致其在问题分析时缺乏必要且科学的主动性，最终形成了思维僵化的问题，无法做到举一反三.

而特殊化策略的运用，则能够实现学生思考问题的角度转变，确保其在问题的分析过程中能多层次探求特殊情形，实现其思维灵活性、广阔性的增强，实现自身思维能力的提升，从而为数学教学目标的实现奠定基础，促进更高效益的取得.

例2a、b、c是不全等的任意实数，若c=a2-bc，y=b2-ac，z=c2-ab，则x、y( ).

A.都不小于0 B.都大于0

C.至少有一个大于0 D.至少有一个小于0

在进行该类问题解答的过程中，学生往往进行式子的转换，进而忽视了对于特殊数值取值的方法进行解答.在这道题目中，学生能够发挥其灵活性，将a设定为0，b为1，c为-1进行该题的解答.在这样的状况下，学生可以排除选项D，随后学生再设定a=0，b=c=1，则x=-1，y=z=1，又可以排除A、B，所以答案选择C.

随着相关教学理念的转变以及教学方法的运用，我国的特殊化策略必将能够融入到数学教学过程中去，并由此实现教学质量的提升，确保初中数学教学工作符合时代发展的需要，促进学生的全方位进步，谋求更高的教学效益.