一二维分片势阱问题的谱元法高效求解

北京计算科学研究中心 刘 焱

薛定谔方程是数学与物理中经典的问题，它描述了波函数量子行为，在流体力学、固体物理、电磁学、量子化学、凝聚态物理及光学等广泛领域内有着重要应用。

无序势阱定态薛定谔方程的波函数会出现高度局域化现象，该现象在相关物理领域中称为安德森局域化。安德森局域化的研究已经有五十年以上的历史，但依然有很多相对开放的研究课题。

2016年，DouglasN.Arnold提出，在无序势阱的条件下，薛定谔方程的特征值及特征函数局域化区域，可以由求解相应的源问题进行预测，并给出了理论上的部分证明。Arnold以分片常数随机势阱模拟无序势阱，利用三次有限元方法完成了一维和二维的数值算例，得到了经验性的结论，但数值结果的精度低，规模小。

考虑单位方形区域内，零边界条件下简化的薛定谔方程及其对应的源问题：

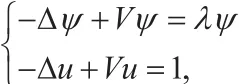
其中，V为势阱函数。

逼近无序势阱要求使用大规模分片势阱V，有限元方法难以完成对大规模相应的特征值问题及源问题的数值求解。针对大规模分片势阱薛定谔方程及源问题，本文提出了高效的谱元法数值格式，并设计快速算法，得到了一种低计算量、高效且高精度的数值方法。利用该高效数值方法，本文在同等精度要求下，完成了更大规模的数值算例求解。

本文结构主要分为两个部分：第一部分，我们基于势阱分布完成了网格剖分，发展谱元法提出了数值格式，设计了相应的快速算法。第二部分，在一维及二维的数值实验中，我们首先检验了谱元法的有效性及相对有限元的优越性，然后验证了安德森局域化现象，最后完成了对特征解预测理论的高精度数值研究。

一、无序势阱问题的谱元法

源问题预测特征解的部分理论支持参见DoulasN.Arnold所著的相关文献，因此本节仅描述数值方法。

首先，对无序势阱使用分片常数随机势阱进行逼近。不失一般性，对一维单位区间[0，1]进行均匀剖分，多维区域由一维区域分解张量形成。使用在每个子区域内取随机常数的分片常数随机势阱来模拟无序势阱。

源问题与特征值问题的变分形式及逼近格式不再赘述，重点描述基函数的选取。

参考沈捷等人的著作[5]中节4.1.2的内容，引入在[-1，1]上的基函数，这组基函数满足刚度矩阵为单位矩阵，质量矩阵为三带宽五对角矩阵。在此基础上进一步优化，于是得到一组新的基函数，其对应的质量矩阵与刚度矩阵均为对角阵。结合有限元对区域选择的灵活性与谱方法的高次数高精度特性，生成谱元法基函数，进而拼接得到一维全局谱元法基函数，而二维逼近空间的基函数即为一维基函数的张量积。

得到基函数与逼近空间后，将问题转化为离散问题线性系统。

以二维情况源问题对应的线性方程组为例，说明谱元法对应的快速算法的核心内容。

基于Schur补的思想，通过一个恰当的置换矩阵，我们将线性方程组重排为：

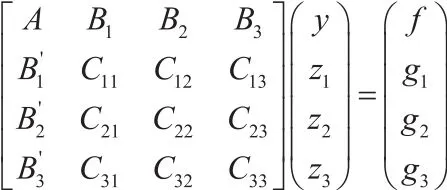
其中，矩阵块A为对角矩阵，其他矩阵块为稀疏矩阵。利用线性有限元，分别在xy两个方向及单独一个方向替换谱元法，我们可以得到z1，z2，z3的低精度近似解。利用矩阵块A我们可以得到y的近似解。于是我们得到线性方程组的预条件子，结合共轭梯度法，我们便有高效的迭代求解算法。

二、数值实验

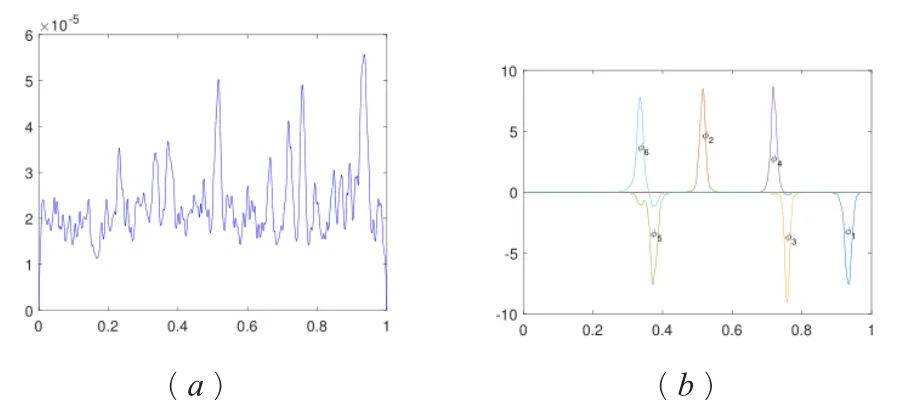
图1 概貌函数（a）及前6个特征函数（b）

本节主要介绍特征值问题与源问题在一维与二维下的数值算例。所有数值实验均使用C语言进行并行编程实现。数值结果中，一律以参数（P，M）分别表示分片常数随机势阱的随机最大值与单个方向分片区域个数。所有未单独标注的数值算例均经由N=10次分片多项式计算得到。

1．一维算例

一维算例均在工作站上完成，使用cpu核数为8。取（P，M）=（10e5，300）的分片势阱V来模拟无序势阱。

源问题的解（又称概貌函数）和前6个特征函数的图像如图1所示。

从图1中可以观察到特征函数的高度局域化现象。叠加两图对比可以观察到，每一个特征函数均对应局限于概貌函数的某一个波峰内。这两种现象前者对应安德森局域化现象，后者对应概貌函数的控制理论。

对于（P，M）=（10e5，300）的一维特征值问题算例，采用基函数次数N=30的算例作为参考解，检验一维情况源问题对特征值的预测结果。

?

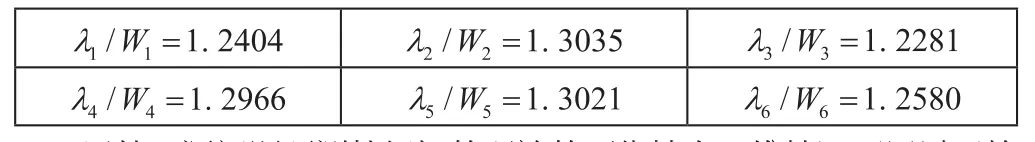
显然，源问题预测特征解的理论的可靠性在一维情况下通过了检验，且数值结果与经验性结论吻合。

2．二维算例

二维情况取参数（P，M）=（10e5，100）的算例来验证概貌函数对特征的控制理论及预测理论。

图2 概貌函数a及第一个特征函数（b）的等高图

图2展示了概貌函数与第1个特征函数的等高图对比，我们发现特征函数的局域化区域可以被概貌函数预测。此外，结合参考特征值，可以得出概貌函数对特征函数的控制结论。

?

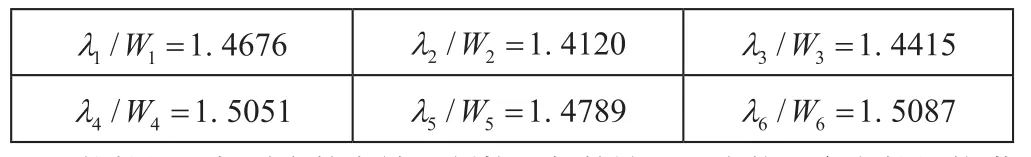
将特征函数对应的有效限制势函数的波谷最小值与参考特征值进行对比，得到如上表所示的源问题对特征解的二维预测结果。

本文针对传统有限元难以求解大规模势阱问题及源问题的现状，提出了谱元高效数值格式并设计了快速算法，完成了一维及二维情况下的大规模数值实验，得到了更高精度的数值结果。本文提出的数值方法尚有进一步拓展的潜力，未来我们拟将该谱元方法应用于三维数值实验，从而填补三维情况下的数值研究空白。