利用《几何画板》微课做数学实验的功用性和价值性

福建省龙岩第一中学 张垣功

在教材中设置了大量数学动手实验,主要是通过创造问题情境,认知现实生活，设计实验模型等环节提出。然后，通过问题导入的实验，以自身掌握的知识和经验为基础，主动地建构数学概念；通过观察验证的实验，以教师启发的互动和推理为手段，积极地发现数学定理；通过合情类比的实验，以教材提供的例题和习题为母题，有效地拓展问题结论。本文就《几何画板》微课在数学实验教学中的功用与价值等方面谈一些看法。

一、利用《几何画板》微课做数学实验有助于学生加深对概念的理解，对要领的掌握

在数学概念教学中，我们经常会受概念的引入和形成所困惑，对数学概念的本质属性挖掘不到位，因某些数学概念抽象，往往是知其然而不知其所以然，为了让学生能理解某数学概念的发生、形成和发展过程，真正理解概念的本质属性，这就要求教师在课堂上讲解概念时应根据学生已有的知识背景和活动经验，展示一些操作、实验、观察活动，让学生思考、交流、反思等过程。

如在讲二面角的概念时（如图1），可以用《几何画板》软件做一个微课实验：拖动点A，则点A所在的半平面也随之转动，即改变二面角的大小和位置，图形的直观变动让学生观察在各个不同位置时二面角的图形特点，有利于帮助学生建立空间观念和空间想象力，从而加深对概念的理解。

又比如在讲椭圆的概念时，可以用《几何画板》微课画2个定点F1，F2和线段AB的长为定值。然后在线段AB上取一点E，分别以F1为圆心，AE的长为半径和以F2为圆心，BE的长为半径作圆。让学生猜测和探讨两圆的交点轨迹。学生各抒己见之后，老师拖动E点在线段AB上逐步双向慢速移动的演示，也可以设置点E在线段AB上双向慢速移动的一个动画按钮演示，学生豁然开朗：“原来是椭圆”，且其运动轨迹是逐步在不断追踪点E而形成的。接着老师用鼠标拖动点B（即改变线段AB的长），使得|AB|=|F1F2|时，满足条件的点的轨迹变成了一条线段F1F2。当|AB|＜|F1F2|时，满足条件的点的轨迹则不存在。通过上述实验的演示与操作，问题情境的创设以及学生的讨论回答，使学生对椭圆的概念会有一个清晰准确地认识和全面深刻的理解，不仅使他们知其然，更能知其所以然。

二、利用《几何画板》微课做数学实验有助于学生发现数学原理、猜想数学结论

在数学定理教学中，如何合理讲授和推出数学原理是经常茫然的课题，其教学方法大都是直接给出原理的内容，没有注重知识原理的来龙去脉，对学生的思维形成产生不良的效应，同时，对原理的应用也浮在表面，甚至使学生一知半解，似懂非懂，造成感知与概括之间的思维断层，学生只记着课本提供的公式、定理，然后简单套用，完全处于一种被动地位，这就要求教师在课堂上充分利用多媒体手段把原理的发生和发展过程展示出来，并揭示原理形成的规律。

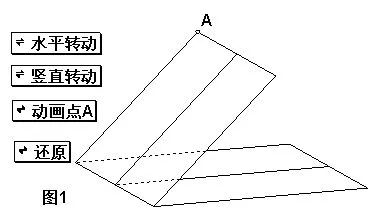
图1

例如，在讲解高中新课程必修4（人教版）第154页的例4时，可以用《几何画板》软件做一个微课：求已知圆的内接矩形的最大面积，即设置这样的一个动画：画一个圆O，作任一半径OA，在OA上取一点C，过点C作EF⊥OA交⊙O于点E，F，过点E，F分别作EH∥OA，FG∥OA交⊙O于G、H。连接G、H。接着使点C在线段OA上双向慢速运动，观察圆O内接矩形EFGH的面积的度量值，发现点C在线段OA上运动过程中，矩形EFGH的面积值是先增后减。反复演示，并请同学们注意，面积取最大值时，此矩形会有何特征？先猜想、讨论，后显示EF和GF的度量值，得到结果是正方形，再从理论上加以证明。这样，学生就能主动地在轻松又活跃的课堂气氛中猜想数学结论，再根据这个结论设置相应的动画按钮（如图2和图3），通过变换不同的位置，得到相同或不同的数量关系，从而推出相应的结论。用同样的手段和方法对多面体、旋转体的截面面积进行探索就能发现其统一的内在原理。

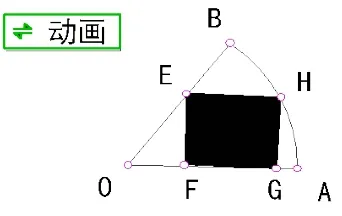
图2

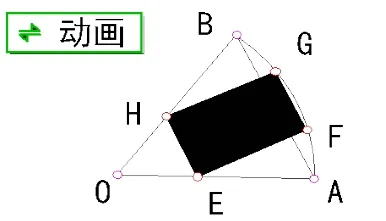
图3

三、利用《几何画板》微课做数学实验有助于学生探究数学规律、验证数学知识正确与否

在数学探究教学中，恰当改变、增减数学试题的条件或结论，让学生体会数学问题的精彩，体验学习数学的乐趣，积极主动学习有价值的数学，也是值得教师思考的话题，因此在教学中，教师努力创设《几何画板》微课，根据学生的实际认知水平及课程标准，对教学知识进行整合、重组、补充、加工，使学生能感受数学应用的实际意义，构建课堂的有效性。

如线性规划教学中求目标函数的最值，可以利用几何画板的移动、旋转、测算功能，使与目标函数所在直线平行的直线在任何一个位置，一边移动（转动），一边测算其值。观察最值的位置，确定最优解。如图4点击，移动按钮，画面将出现一组平行直线（一束直线）和相应的数值（如图4）。

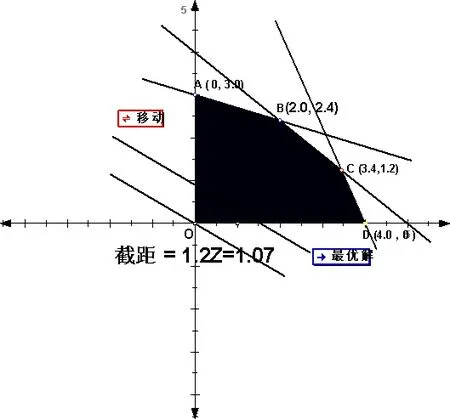
图4

四、利用《几何画板》微课做数学实验有助于学生找到解决问题的有效途径，拓展数学问题的结论

数学结论与求解过程是教学过程中一对十分重要的关系。展示教学过程能唤起探索与创造的欢乐，激发认知兴趣和学习动机；展现思路和方法，教人怎样学习，它能帮助我们提高学生的创新能力。利用《几何画板》进行数学实验教学是一种让学生经历知识探索过程，发现新认识、新信息，提出新问题、解决新问题的创造性学习。因此，在数学课堂教学中，发现学生解题时因为找不到突破口而困惑，可以引导学生通过数学实验来发现规律，从而获得解题的多种途径。

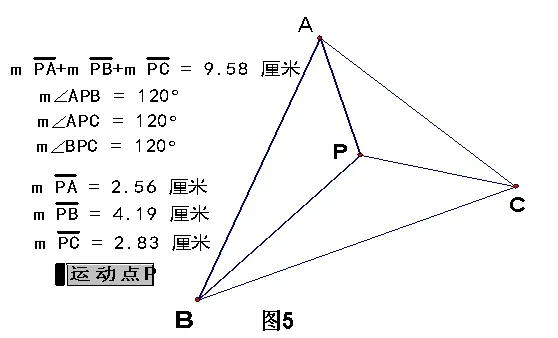
图5

又如：设M（x1，y1）为椭圆x2+2y2=2上的任意一点，过点M作一条斜率为的直线l，又设d为原点至直线l的距离，r1，r2分别为点M到椭圆两焦点的距离。试证明：常数。其解答可用代数方法顺利解决，此题若作深入分析，引入《几何画板》辅助教学（如图6），必让学生学有所得。

探索：“测算”MF1和MF2与直线l所成角的大小并列展示在平台上，提示学生注意两角关系，当点M再次运动时，发现这两角保持相等。说明MF1和MF2存在反射关系。可方便进行实验：过M作直线l的垂线（法线），并标记镜面，构造点F1关于的对称点，结果看到点在射线AF2上。

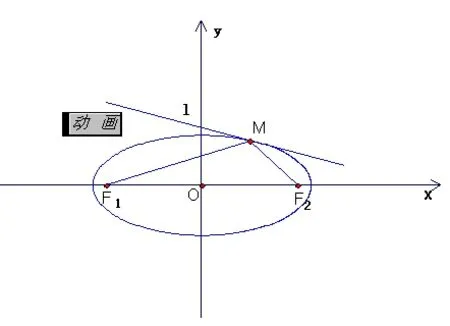
图6

再探索：例题中椭圆x2+2y2=2改为双曲线x2-2y2=2，结论还会成立吗？重复以上操作，学生惊奇地发现结论是如此相似，直线l还是双曲线的切线，依然是定值。

总之，使用《几何画板》微课做数学实验教学，通过具体的感性的信息呈现，能给学生留下更为深刻的印象，使学生不是把数学作为单纯的知识去理解它，而是更有真实感地去把握它。这样，既能激发学生的情感、培养学生的兴趣，又能大大提高课堂效率。