数形巧结合——数学抽象变具象

安徽省宣城中学高三（12）班 杜 偶

众所周知，数学是一门极具抽象的学科，对于我们抽象思维程度不高的高中生来说，抽象的数量关系、数学概念等是难以理解的。既然现代数学是一门以研究数量关系和图形为主的学科，那么在学习数学知识的时候，我们可以在数与形的转化下，借助直观的图形展现抽象的数量关系，借助具体的数量关系赋予图像以实际意义，借此加深对数学知识的理解，探寻到解题方法。那么在高中数学学习活动开展中，我们要如何应用数形结合这一思想方法呢？

一、在新知学习过程中，初探数形结合思想

在数学学习活动参与中，我们往往会遇到两种知识，一种是表层知识，一种是深层知识。所谓的表层知识是指数学概念等极具基础性的知识，而深层知识则指数学思想方法。这两种知识是相互依存，相伴而生的。也就是说，在进行表层知识学习的时候，我们常常会看到各种各样的数学思想方法。为了加深对表层知识的理解，我们需要在教师的引导下自主地将数学思想方法引入其中，借此在自主探究过程中掌握数学学习方法。以“集合间的基本关系”这节内容学习为例，我在学习集合知识的时候，对课堂上教师所讲解的集合概念不甚理解，对此，我借助韦恩图来表示各个集合之间的关系。以A={1，2，3}，B={1，2，3，4，5}这两个集合为例，我借助韦恩图做出了这样的图（如图1）。

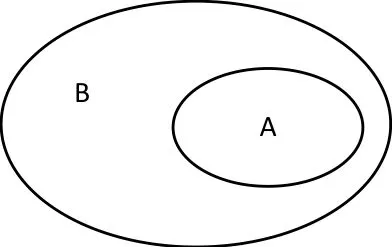
图1

在直观的图形展示下，我不仅看到了这两个集合之间所存在的关系，还对子集产生了一个感性的认知，为新知学习打下了坚实的基础。

二、在问题解决方法探索中，巩固数形结合思想

我们学生学习数学知识的一大目的是运用所学的数学知识解决实际问题，这是毋庸置疑的。对此，在参与数学学习活动的时候，我们需要树立起数学应用意识。要想对数学知识进行运用，掌握有价值的思想方法是必不可少的。在高中数学学习活动参与中我们可以发现，数学中存在着大量的数与形，二者是数学研究最基本的对象，而且呈现在我们面前的数学问题大都与数与形有着直接的联系，加之数学思想方法是指导运用所学解决数学问题的有效方法，所以在解决数学问题的时候，我们要树立起数形结合意识，在数形结合思想方法的作用下，实现数与形的相互转化，进而在降低数学解题难度的基础上，实现所学知识的灵活运用。以这一求解不等式问题为例，在过去，我一般会直接借助数学计算方式直接进行计算。尽管这样的计算方法能得出最终的结果，但是，由于多种因素的限制，在计算的时候常常会出现错误，导致计算失败。对此，在数形结合这一思想方法的引导下，我会借助不等式问题转化为几何意义，借助数轴的方式将其呈现出来，然后在直观的数轴作用下探究结果。

经过对题目进行分析我发现，该问题的几何意义是：使得x到点2和点-3之间的距离之和大于7的x的取值范围。接着，画出这样的数轴（如图2）：

图2

在直观的图形作用下，我们可以看到，当x≤-4或x≥3的时候，不等式成立。如此，在数形结合思想方法的作用下，解题步骤简单化，有利于提升解题效率。

三、在知识归纳总结中，概括数形结合思想

数学思想方法是以数学知识为载体的，对此，在学习数学思想方法的时候，我们需要以基础的数学知识为依据。纵观我们所使用的数学教材可以发现，各个知识点是按照螺旋上升的趋势编排的，而蕴含其中的数学思想方法则是较为分散的。对此，在数学学习活动参与中，我们需要在一段学习时间之后，以专题复习的形式将有关的数学知识建构一个系统的结构，并在系统知识归纳总结中，探究数学思想方法。我在该环节，一般会从以下两个方面进行知识总结：第一，在近期所学到的数学知识中有哪些内容涉及了数形结合思想，比如在集合学习中运用韦恩图、数轴，在不等式解决中运用数轴，在函数最值求解中运用函数图像等。在这样的知识总结中可以为我们的解题积累经验，一旦遇到与之有关的问题，则立即选择数形结合这一思想方法解决问题。第二，归纳总结近期运用数形结合这一思想方法解决问题的过程中所存在的问题，诸如数形转化的等价问题、图像分类情况等，借此在有的放矢中提高数形结合思想方法的应用效率。

总之，在高中数学学习活动参与中，我们要借助多样化的方式将表层知识与深层知识结合起来，在数学思想方法的引导下加深对基础知识的理解，并在数学思想方法的指导下运用所学的数学知识解决数学问题，为学以致用的实现打下坚实的基础。