浅析利用数学问题解决培养学生的创新意识

福建省南安市康美镇福玲中学 黄育钞

教师和学生进行沟通和交流主要是教学技巧，教学技巧反映着教师创新的教学意识和综合的教学水平，教法巧妙就能使学生及时准确地理解和掌握所授的内容，并有利于拓宽思路、发展思维能力，达到与相关知识融会贯通的效果。教师如何使课堂教学生融情入境；如何利用教材对学生进行思想训练，培养学生发散思维的能力；如何创造有活力、富有情感的教学，还需要教师刻意求索，用心总结。下面以我在教学中的实际谈点体会。

一、引而不束

指导即指点引导，指示教导。古人曰：“善教者，善导。”教学的真谛是教师教学生如何学。这犹如教师把打开知识大门的钥匙交给学生自己去把握，去开启。因此，在教学过程中，教师要善于通过指导学生学会自学、学会观察、操作、分析，学会自立等方面来全面提高学生的求学能力。

例如，“三角形全等的应用”一节的教学设计如下：

在国家为搞活经济，大力推行旅游事业，促进各种文化的相互了解、比较，为我们相互学习提供肥沃土壤的今天，我常利用双休日出去小游。一次在某个旅游点游览时发现一湖，我想到家乡农民朋友浇地难的情境。假如在农田附近建一池塘，用来解决农作物旱涝之急，该多好！于是我想预测一下此湖的宽度，可又细睹了湖面，发现其宽度甚大，难以测量，同学们想想看，有没有办法来测量湖宽呢？同学们有的说，用绳子绕湖转一圈。还有的说，跳到湖里用绳子从这头拉到另一头……为保证安全，第二种方法不可取，而第一种方法又不可靠。我们要知道，钻研尖端科学是有困难的，但绝不是可望而不可即的。方法是：

如图1，有一池塘，要测池塘两端的A，B间的距离，可先在平地上取一个可以直接到达A和B的点C，连接AC并延长到D，使CD=CA，连接BC并延长到E，使CE=CB，连接DE，那么量出DE的长，就是A，B间的距离，为什么？

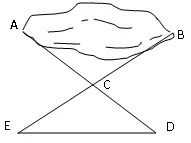
图1

通过此例，学生们就会从猜想转向逻辑思维的思路上。但教师要鼓励学生的求异思维，让学生的思维发散开去，再适时聚敛到课本中来，把思维的抽象力和正确的思考力应用在理论上，这比将“冷冰冰”的例题搬出有“人情味”，更有美学价值，使课堂教学既不失控，又不僵化，这节课就会“导”出学生思维活跃的精彩场面。

二、诱而不替

引导即引路导向。俗话说：“施教之功，贵在引导。”无论是新课引入，还是新知识、新问题、新思路、新方法的引出，都需要教师根据学生的实际，采取各种行之有效地方法进行灵活多变的引导，使学生尽快“上路”，进入“角色”。

求证：三角形外角和为360°。

此题一出，学生凭借直觉和证题经验，是很难找到良好的证明方法的。为使学生能从多方位，多角度地进行定理证明，我将学生分成两大组，各组学生要求分别画出锐角三角形，钝角三角形和直角三角形的图形，然后略作提示，问：在特殊角中，什么角为360°？在折纸求三角形外角和时，你发现了什么？大家可围绕这两个问题展开思考。待学生发现折纸中的情境时，教师穷追不舍逐步逼近。不妨在三角形中增添些平行线，看能否将三角形的三个角转向一个周角位置？学生对各自所画的三角形仔细推敲，捕捉事物的内在联系，最后各组同学都相应地得出了不同的证法。如图2。

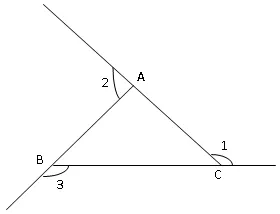
图2

教师再提问：①你能用“三角形的内角和等于180°”来说明∠1+∠2+∠3=360°吗？②你有用“平行线的性质”来说明∠1+∠2+∠3=360°吗？

这样学生从不同的角度完成了定理的证明。正当学生心存侥幸时，我认为不要急于肯定总结方法，更为重要的是，要组织学生从证明法中总结证题思路的有效程序，让这些知识内化成认识事物的方法。教育学生在考虑问题时，不要拘泥于某框架范围之中，要大胆设想，勇于创新，要养成良好的思维习惯，使自己向智能型人才的方面发展。

如：在本节学生认识到上述证明思维方式各有特点，不尽相同，彼此间并无高下之分，且是辅助相成，殊途同归而心驰神往时，我将学生引向另一个角度。请大家来猜一猜谜语，谜语是“一刀破断后只有一截”，这是什么？多数学生说，一切都具有“一刀两断”的性质，哪有一刀一截的可能？这时，我拿出事先准备好的圆圈，示范着动作，学生们恍然大悟。此时教师可提醒学生，谁顽固地认定某东西“一定”是某样子，谁就犯了“僵化”的错误。随着这一脑筋急转弯的势头让学生进入下列证明。

已知：如图3，三角形纸片ABC中，∠A=65°，∠B=75°，将纸片的一角折叠，使点C落在△ABC内，若∠1=20°，求∠2的度数。

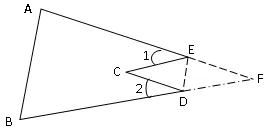
图3

此题一出，立即触及学生思维火花的引爆点，使学生悟出证明三角形内角和定理的异径。同时使学生领悟到，评价证题的方法，不能单靠殊途同归法，还要思考还有没有其他方法，要“吃一堑，长一智”。

三、抛砖引玉

“因式分解综合课”的设计：今天，我给大家带来一个故事。从前有一个国王，他有两个儿子，他想选择一个儿子来继承王位，可他的两个儿子的才气相当使他左右为难。一天他终于想到了一个办法，然后他选群臣相聚的良辰吉日，他说：“今天有一个考题，需要谨慎思维，谁今日擂主，智力显神威。”题意是：今有两缸，差异甚微，要将大缸套入小缸，大家想想是否可以？

此题一出，他的小儿子立即解答了这一问题。其父听后欣然大喜，并当众宣布从今日起由小儿子来继承王位。

同学们，你们猜到了吗？一部分同学答道：把大缸打碎装在小缸里。我赶快祝贺他们答对了。那答错的或没答的是何原因呢？答案是：他们是受思维惯性的影响。因他父亲并没说不可将缸打碎，只要求将大缸套在小缸里。打碎了又有何妨？好，这节课就借这个故事来剖析因式分解的题型。

例：把下列各式因式分解。

（1）(x2+2x-4)(x2+2x-2)+1；

（2）x2-（y-2）2+2（x+y）-4。

学生纷纷展开思维，思维过程中，学生尝试了单靠前几节学到的知识把多项式当作因式来分解的方法是解决不了这几道题的。他们敢于冲出思维的惯性圈，大胆设想，勇于创新，有不少同学选准思维的另一个角度，别开生面地找出了解题的途径。最后教师归纳总结各题的特点和方法，使学生在反思过程中注意训练心智，不断刺激思维发展，使之能正确而活泼地思考问题，得到多方位、多角度的收获。教师要告诫学生，事实表明，谁受思维定势的束缚，谁就可能在思维时作茧自缚，这对我们的创新思维十分有害，希望大家要警惕这一点。也希望大家能与社会并行发展，创造出奇迹般的新意，让人们共享财富，共享成功。

最后，我想说的是，社会发展需要大批创造型人才，创造型人才最重要的特征就是具有创造性思维。因此，作为教师，在指导学生学习时，要时刻提醒学生：思考问题切忌作茧自缚！也只有摆脱了思维定势，不受思维惯性的束缚，才能使思维更流畅，更灵活，更有创造性！