简朴中显特色 平凡中见真谛——2018年高考全国Ⅰ卷（理）第16题解法赏析

江西省南康中学 许钤川

纵观今年的高考数学全国Ⅰ卷试题，虽然知识点覆盖比较全面，但整体难度并不大，并无所谓的“偏题”“怪题”。大部分题目考查学生对知识的熟练程度，但第16题更多地考查了学生的逻辑推理能力和思维灵活性，检验考生数学核心素养的高低。其横向入口较宽,纵向难度较大,灵活性、综合性都很强。下文是笔者对这道试题解法的一点探究,意在抛砖引玉,切磋交流.

题目：已知函数f（x）=2sinx+sin2x，则f（x）的最小值是 。

分析：有些考生可能会想到三角函数的相关知识，想要化简合并，以求最值，但却失败。为什么失败？因为他们陷入了一种思维定势，认为这就是一个三角函数的题目，要用相关的三角函数知识去求解，结果深入不下去。而有些学生看出了端倪，这个题目只是借用了三角函数这样一个载体，或者说是一个障眼法。直接求导求解，最终成功。这个例子很好地告诉了我们“灵活”二字在高考当中的重要性。下面我们来说几种关于这道题的较为灵活的解决方法：

方法一：求导法

首先说的是常规求导法，即求出函数的导数，令导数为0，求出极值，极值与区间端点处的函数值进行比较，最大的就是最大值，最小的就是最小值。

解：因为f（x）的周期为2π,所以可以在一个周期[0,2π)内讨论。

方法二：均值不等式

均值不等式也是高中常用的方法，在这个题目中也可以使用。虽然比较难想到，但对于成绩较好或者参加过奥赛的学生来说也不失为一种好方法。

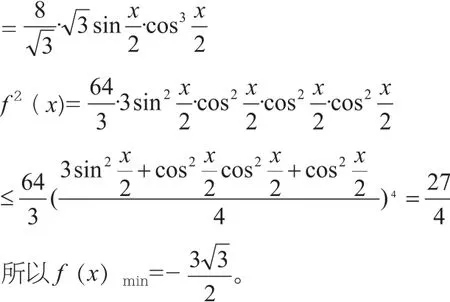
方法三：万能公式法

若熟悉万能公式,还可以用如下方法：

当 t=0 时，g（t）=0；

方法四：琴生不等式

如果学习了奥赛知识，了解了琴生不等式，用来做此题，也不失为一种很好的方法。

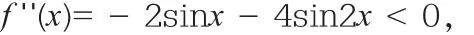
所以f（x）=2sinx＋sin2x=sinx＋sinx＋sin（π-2x）

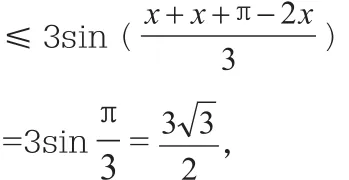
综上，本题虽小，但入口宽，解法具有开放性、探究性，体现了新课程标准理念和教材的设计意图。简朴中显特色，平凡中见真谛。提高了考生的观察思辨能力，提升了本题的考查功能与选拔功能，很有开发价值，无疑是一道经典之作。