关键卡在哪儿？——一道中考数学题的命题与解法

山东省日照市五莲县教学研究室 王金凤

一道命题巧妙、立意独特的中考试题能够更加准确地检测出学生的真实水平，更好地发挥升学筛选的作用，同时还可以对教师的数学教学起到引导作用。重庆市2015年数学中考试卷第25题给我们的感觉是第三小题的图形很复杂，证明起来难度较大，那么如何才能降低题目的解答难度，解题的关键在哪里？这是本文尝试探讨的问题。

一、试题介绍

（2）试证：HP =HF。

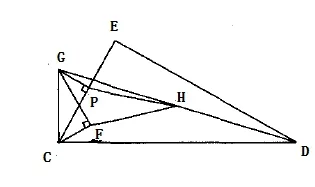
图1

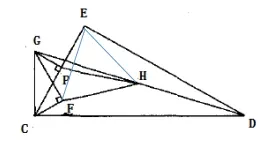
图2

二、分析与解答

问题（1）中，已知∠CED为直角，∠DCE=60°，根据勾股定理可知CD=2CE，而CE=，因此，CD=，DG=。问题（2）比问题（1）难度稍大，需要添加一条辅助线，如图3所示，并进行简单推理，考查的是基本技能。

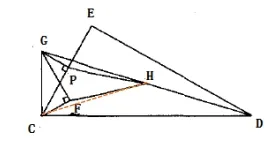
图3

如图3，添加辅助线CH，GP=CF，GH=CH，因为∠FCH=∠FCD-∠HCD=30°-∠HCD；∠HGP=∠HGC-∠PGC=∠HGC-60°=（90°-∠HDC）-60°=30°-∠HDC，可得∠HGC=∠HGP，△PGH≌△FCH，证得HP =HF。

问题（3）保留了问题（2）的线段，少了点P是CE中点的条件，属于开放式命题，考查的是综合能力，难度较大。

证明：如图4所示，取CD中点K，连接EK，HK，在直角三角形△中，CG =2CF，HK是△CGD的中位线，因此，CG =2HK，可知△为等边三角形，故CE=EK，又因为∠ECF=∠DCE=30°，∠EKH=∠CKH－∠EKC=30°，可知△ECF≌△EKH，所以∠CEF=∠KEH，∠CEF+∠FEK=∠KEH+∠FEK=60°，可得△FEH为等边三角形。

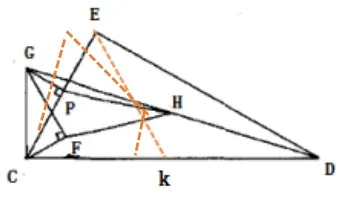
图4

该方法充分利用两直角三角形的中点构成中线和中位线，并构造全等三角形，从而联想到几何变换，引出了上述的证明思路：添加辅助线，通过证明△FEH有两条边相等，再证明其中一个角为60°，从而证明其为等边三角形。从几何变换角度来说，如图4所示，证明了一对全等三角形，相当于△EFC绕点E旋转得到△EHK。通过图4的证明方面，我们可以看出图2有瑕疵。

综合性几何题目为了呈现各个题目之间的关联，体现从易到难的命题原则，通常需要组合多个知识点以及图形拼接、叠加等。但是，图4的证明方法没有用到图2中的线段GP，HP，为什么不将图2的线段DH、FH抹去呢？通常来说，题目条件越多，解答难度越低，而本题的题目条件多了，难度却增加了。

三、几何变换是关键

如何将问题（3）中的图形进行简化，证明的关键在哪里？我们将把图2中线段GP，HP去掉，简化图形，在根据旋转或对称性质来证明问题（3）。因此，原题目可以修改为：如图5所示，在△CDE中，∠CED为直角，∠DCE=60°，点F是∠DCE平分线上的一点，经过点F作GF垂直于CF，过点C作GC垂直于CD，GF，GC相交于点G，连接GD，点H为GD中点，GP垂直于CE，垂足为点P，连接HP，HF。

（1）GP垂直于CE，垂足为P，若H为GD的中点，CE=，求CD，DG的长。

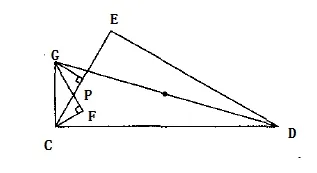
图5

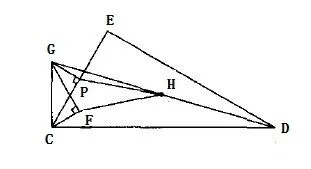
图6

（2）如图6所示，DH⊥AC，垂足为H，连接EF，HF，求证：HF=EF。

图7

（3）如图7所示，连接EF，EH，FH，△EFH是否为等边三角形？如果是，请证明；如果不是，请给出理由。

通过将原题目变换为现在的三个图形，对于突破难度较大的原题第3问更加有力，同时能够更好地实现命题者的考试意图。中考命题的根本目标是有效地检测学生的实际水平。因此，命题者应该从“理解学生”和“理解数学”出发来进行中考命题。经过修改后的题目，既不影响继续用图4的方法，还有利于发现如下更多的方法。经过修改后的题目，不影响继续用图4的证明方法，还有利于发现更多的证明方法。

我们可以看出该题的解题关键在于几何变换。图4中，△ECF绕点E旋转到了△CMF。基于这种思路，我们很容易想到，△ECF还可以绕点C顺时针方向旋转60°来证明，也可以利用对称来证明，在此，证明过程不再赘述，有兴趣的读者可以自己尝试来证明。

综上所述，我们在进行教学时，不要漫无目的地讲解和学习各种解题思路和方法，而是要仅仅抓住几何变换这个解题关键去分析才是正道。