对称三势阱玻色—爱因斯坦凝聚体的非线性效应

舒鹏丽，王燕锋，雒卫廷

(吕梁学院物理系，山西吕梁 033000)

自1995年首次实现碱金属气体原子的玻色—爱因斯坦凝聚[1]以来，原子间的非线性相互作用就成为研究者关注的内容之一。双势阱的BECs 体系作为研究量子非线性隧穿行为的重要模型[2]，引发了很多迥异的物理现象，如能级的拓扑结构[3]，非线性不稳定态的存在[4]等，特别是非线性约瑟夫振荡和自囚禁现象[5]，实验中用BEC 的吸收谱直接观测到这一现象[6]。随着研究的深入，有不少工作致力于三势阱的BECs 体系[7]，使得人们对BECs 的宏观量子隧穿效应有了更深刻的理解。对于三势阱的BECs 体系，利用平均场近似得到的Gross-Pitaevskii 方程和经典哈密顿理论[8]，来研究复空间的量子波函数和非线性的量子演化。本文从非线性薛定谔方程出发，在一定的初值条件下，研究粒子在三势阱中出现的几率密度随非线性作用的演化关系。

1 物理模型

三势阱中的BECs 在平均场近似下，可以用Gross-Pitaevskii 方程[4,8]来描述，其中GP 方程的波函数ψ(r,t)是3个势阱中波函数的叠加，表示为：

其中，φj(r)可看作第j(j=1,2,3)个能级的基态波函数，aj(t)=是概率幅，满足

经代换，三势阱的BECs 体系可用非线性Schrödinger方程[9]描述：

假设第二个势阱的零点能为0，γ和-γ是第一个势阱和第三个势阱的零点能，c是原子之间的相互作用强度，在讨论中，设c>0，即原子之间相互排斥，v是三势阱间的耦合常数。式（3）多出了原子相互作用导致的非线性项这时候Schrödinger 方程式（2）不能解析求解，只能从数值上研究[10]非线性项所带来的物理效应。

2 对称三势阱，即γ=0

2.1 几率密度在强弱非线性作用下的变化

从图1 可以看出，在弱相互作用c=0.4 下，粒子在3 个势阱间出现的几率呈现Josephson 振荡。(a)初始时，粒子都放在第一个势阱中，随着时间的演化，粒子可通过第二个势阱隧穿到第三个势阱，然后再隧穿回来；(b)初始时，粒子都放在中间势阱中，粒子可隧穿到两边的势阱，且左右势阱呈现相同的振荡周期；(c)初始时，粒子均匀分布在相邻的两个势阱中，势阱中的粒子都可隧穿到第三个势阱中，但是中间势阱的隧穿概率明显小于左边势阱；(d)初始时，粒子均匀分布在不相邻的两个势阱中，两边势阱中的粒子可隧穿到中间势阱中，且左右势阱具有相同的振荡周期。另外图1(b)和(d)显示，粒子相对势阱对称放置时，振荡具有相同的周期。

图1 几率密度pj在弱非线性作用下随时间的演化

图2(a)和(b)为强相互作用c=5，(c)和(d)为强相互作用c=10，粒子在不同的初值条件下，都表现出自囚禁行为，这和对称双势阱中的BECs 在强非线性作用的情况正好吻合[11]。

2.2 平均几率密度随非线性作用强度的变化

为更好地理解粒子在对称三势阱出现的几率密度随非线性作用的变化，引入平均几率密度，研究平均几率密度随非线性相互作用c的演化关系，如图3所示。选取初值与图1相同。

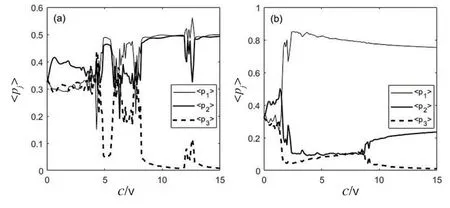
图3 平均几率密度随非线性相互作用c的演化

(a)初始时所有的粒子放在第一个势阱中，当0

(b)初始时所有的粒子放在第二个势阱中，当非线性作用小于临界值时，粒子从第二个势阱隧穿到左右两个势阱中，做周期性振荡，第一个势阱和第三个势阱中的粒子具有相同的振荡行为，随着非线性作用的增大，粒子的隧穿行为逐渐减弱，发生自囚禁现象。

(c)初始时在第一个势阱和第二个势阱中各放入相等数量的粒子，粒子在非线性作用0

(d)初始时在第一个势阱和第三个势阱中各放入相等数量的粒子，第一个势阱和第三个势阱中的粒子具有相同的振荡行为，这两个势阱中的粒子隧穿到中间势阱中，振荡随着非线性作用的增大逐渐减弱，当c>7.8时，粒子被束缚在各自的势阱中。

图3(b)和(d)可以看出，当粒子相对势阱对称放置时，第一个势阱和第三个势阱的粒子的振荡行为相同，约瑟夫振荡和自囚禁现象随非线性作用的增大变化明显。当粒子相对势阱中不对称放置时，图3(a)和(c)，粒子的振荡随非线性作用的变化出现混沌，说明对称三势阱中粒子的行为不仅受到非线性作用的影响，同时也受到不对称初始值的影响。

2.3 混沌可通过改变相位初值转变为自囚禁

图3(a)和(c)发现，当粒子在势阱中不对称放置时，粒子的振荡随非线性作用的变化出现混沌。对方程（2）进行正则变换[4]，对称三势阱BECs 构成的3能级量子系统相应的正则方程为

从(4)～(7)式可以判断p1、p2、p3、θ1、θ2，也可通过正则方程求得，并且p1、p2、p3的值受初始相对相位θ1、θ2的影响。如图4，选取初值(a)(p1=0.7，p2=0.3，p3=0，θ1=0，θ2=π/2)；(b)(p1=0.7，p2=0.3，p3=0，θ1=0，θ2=π)，研究平均几率密度随非线性作用的变化关系。图4(a)中粒子振荡出现明显的混沌区域，改变初始相对相位的取值，如图4(b)，粒子的混沌行为被减弱，振荡较平稳地由混沌转为自囚禁，可以看出相对相位可以控制混沌的产生和转变。

图4 平均几率密度在改变初始相位下的演化

3 结语

利用平均场近似得到三势阱BECs 的非线性薛定谔方程，采用数值求解的方法，模拟在不同的非线性相互作用c下，粒子出现的几率，可得到BECs 相应的非线性隧穿行为—约瑟夫振荡和自囚禁，而且在一定的非线性作用范围内下，粒子出现不规则振荡，即混沌现象，如改变相对相位的初始值，混沌可以平稳地转变为自囚禁状态，这为研究非对称三势阱的非线性效应提供一定的理论基础。