函数图像中的“细节决定成败”
江苏省吴县中学 (215151) 唐俊涛
利用函数图像解决函数相关的值域、单调性、零点问题在高考和各地模拟考试中已经屡见不鲜,而解决这类问题的本质就应该是准确的画出函数所对应的“草图”.有了精确的“草图”,函数中相应的问题就都能够迎刃而解了.
但是在具体解题过程中,学生解题的受阻点往往就是在如何能够“简单精确”的画出函数的“草图”.我们的课堂教学有时因为受到教学进度的影响,在函数图像教学环节可能不够深入,讲解的不够透彻,导致学生对此类问题研究的不深入、不透彻、不全面.
在一次学校组织的月考中有一道填空题:“函数y=2x-1,x∈(-∞,2],则该函数的值域为.”本人执教的两个班级该题的得分并不是很理想,这样的分数与出题者的原本预期有着很大的出入,深入了解后究其原因,发现问题出在多数学生在解决该问题时虽然都是从图像作为切入点,但是作图时往往画的很“草”,没有抓住函数图像的“细节”—渐近线,导致从图像上看函数值域时出现了偏差,本题其实就是将学生熟知的指数函数y=2x整体向下平移1个单位,但是指数函数y=2x本身是有一条渐进线,它与x轴重合了,平日作图时学生不需要单独再添加,可是在将该函数向下平移时,渐近线也应该同时向下平移,所以必须独立添加,不可忽视.但是此时学生往往压根儿没有考虑到,所以最终得到了错误的结果(-∞,3],而非正确答案(-1,3].
既然发现了问题,找到了“惹祸”的根源,那么接下来就必须“痛定思痛”,反思我们的教学,帮助学生减少或者避免这些无谓的失分.可是在教材上虽然在反比例函数、指对数函数、幂函数及正切函数都已经涉及到了渐进线,但是并没有真正意义上的完善渐进线的概念,究其缘由可能是由于现在的教材淡化了极限的内容,所以课堂上教师的教学与学生的学习基本上只是从图像上去直观的感受,这也就导致了学生对渐进线理解不到位,没有达到“数形统一的境界”.可是在平时的练习、考试中、甚至在高考题中,都会有渐近线的出现,所以教师在教学中还是要对渐近线加以强化,从而避免在这一“细节”方面出现无谓的失分.
笔者将常见函数的渐近线做了一下汇总,希望能得到专家的指点:
一、反比例函数的渐近线
反比例函数是初中所熟知的基本初等函数之一,函数有两条渐近线分别为x、y轴,而在高中阶段所涉及的反比例函数往往会将其进行平移,在平移过程中学生就会将原有的渐近线忽略掉,从而导致在判断值域或函数零点的时候出现问题.
例1 (2017年南京高三一模)设函数f(x)为偶函数,当x≥0时,f(x)=
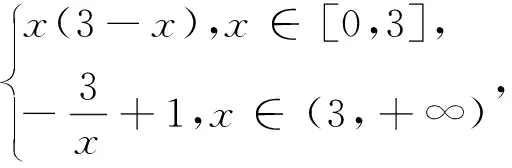
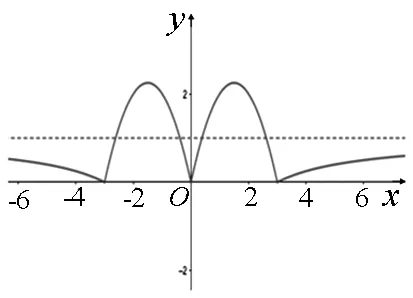
图1
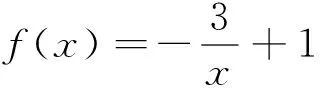


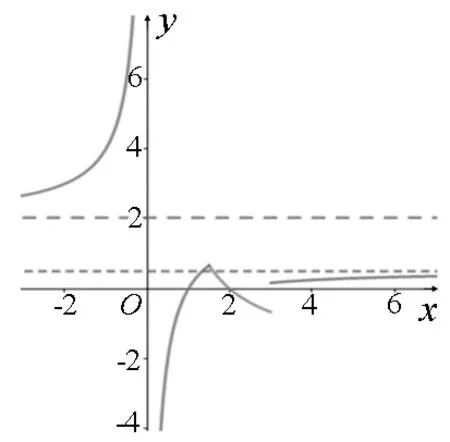
图2
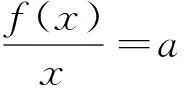
二、指对数函数的渐近线
这里所谓的“指对数型”函数其实是将指对数函数进行一系列的平移变换后得到的新的函数,在平移过程中同样也一定要注意原函数中渐近线的变化.


图3
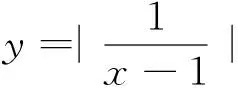

三、含绝对值函数的渐近线
含绝对值的函数在平时练习中也是经常会出现的,模拟练习中含绝对值的函数往往需要学生更加认真的观察,从而去画出准确的“草图”.
例4 已知f(x)=|xex|,g(x)=f2(x)+tf(x)(t∈R),若满足g(x)=-1的x有四个值,则t的取值范围为.

图4
解析:g(x)=-1中可通过换元:f(x)=m,先将该方程转化为二次方程:m2+tm+1=0,此二次方程的根m决定了最终能有几个x,所以同时也需要做出函数f(x)=
|xex|的图像,求导后易得
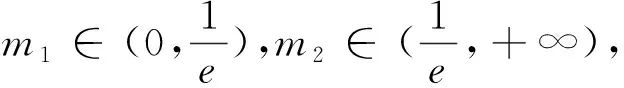
本题易错点是在当x→-∞时,y→0,从而挖掘出渐近线,学生在解题过程中往往看到(-∞,-1)为单调减,函数图像就是从-∞往下“走”.这样处理本题就遇到了“易错点”,而当x→-∞时,函数值涉及了极限的思想,教师可以让学生代入具体的数据从而直观感受函数值的趋势,这样就可以让学生了解x轴其实就是该函数的渐近线.
同时解题过程中也可以让学生自行概括函数渐近线的求法:(1)当x→-∞时,y→c(常数),则y=c就是函数的一条水平渐近线;(2)当x→c(常数)时,y→±∞,则x=c是函数的一条垂直于x轴的渐近线.
四、分式函数的渐近线
分式函数在处理时必须遵循定义域先行的原则,把分母不为零作为研究函数的首要原则,分母为零反映到图像上对应的是x=x0这样的一条渐近线.
例5 (2016年全国卷)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.(1)求a的取值范围;(2)略.
解析:此题方法较多,笔者重点选择介绍渐近线在这题中的应用:

图5
(法二)令(x-2)ex+a(x-1)2=0,(x-2)ex=-a(x-1)2,令g(x)=(x-2)ex利用导数求得g(x)单调区间:(-∞,1)为减,(1,+∞)为增,且当x→-∞时,y→0,所以函数存在渐近线y=0.令函数h(x)=-a(x-1)2,如要使得f(x)有两个零点,即g(x)与h(x)要有两个交点,所以可得a∈(0,+∞).
类似的题目在我们平时考试过程中应该会常见,如:
例6 (2017年苏州高二期末考试)对于函数f(x),若其定义域内存在两个不同的实数x1,x2,使得xif(xi)=1(i=1,2)成立,则称函数f(x)具有性质P,若函数f(x)=aex具有性质P,则实数a的取值范围为.
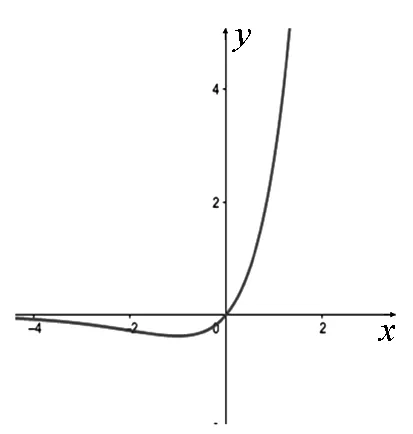
图6
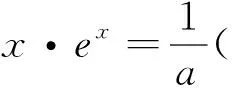
由上述这些练习可以知道,渐近线在我们平时的数学练习中反复出现,存在就有存在的意义、价值,所以我们要把它研究透彻,研究细致.从另一方面讲,渐近线其实不可怕,可怕的是我们没有具备发现、挖掘它的一双“慧眼”,而这双“慧眼”并不是与生俱来,是需要通过不断的训练而慢慢养成的.

