薄膜干涉中半波损失与附加光程差的讨论

曹卫军

（昌吉学院初等教育学院 新疆 昌吉 831100）

在分析等厚干涉、等倾干涉、增透（反）膜等薄膜干涉问题时，经常遇到半波损失和附加光程差的问题。然而，一般大学物理教材对半波损失没有给出详细的解释，只是描述为“光从光疏介质入射到光密介质光反射时，产生π的相位突变，相当于失去了半个波长的光程”[1][2]。涉及到额外光程差的计算时，有的教材中只是粗略地概括给出结论，不给出详细推导，有的教材提到是因为半波损失导致的附加的光程差。正因为如此，关于半波损失与额外光程差的研究有很多[3-17]。可是，这些研究对半波损失产生的条件说法多样，有的比较模糊，有的互相矛盾，令人困惑。下面我们从菲涅尔公式入手，讨论半波损失产生的条件，分析多种情况下薄膜干涉中是否存在附加光程差，并对半波损失与附加光程差的关系进行梳理。

1 概念界定

1.1 薄膜干涉

由薄膜产生的分振幅干涉通称为薄膜干涉。当入射光到达薄膜表面时，被分解为第一束光反射光与折射光，折射光经薄膜下表面反射和上表面折射，又回到上表面空间后得到第二束光，这两束光在薄膜的同侧交叠而发生干涉。在界面出由于反射与折射使得入射光得以分解，从而获得相干光。光的振幅的平方即为光强，所以薄膜干涉属于分振幅干涉，一般分为等倾干涉、等厚干涉两类。

1.2 半波损失

在某些特定条件下，界面上反射光波的光矢量与对应的入射光波的光矢量方向发生了反转，这种方向反转导致±π相位突变，换算为光程突变为±λ 2。这就是所谓的半波损失[18-19]。

1.3 附加光程差

薄膜干涉中，由于光在两个表面的反射的物理性质不同，薄膜在上下两个界面上的相邻两束反射光的电矢量和振动方向相反。计算光程差时，除了由于一定厚度的薄膜反射、折射引起光路的不同产生的光程差以外，还得加上λ 2的额外光程差（也叫附加光程差）。可见，附加光程差是指两束反射光之间的关系。

由于反射和折射所带来的附加的E振动方向变化，其等效的相位或光程变化常称为附件相差或附加程差[20]。

2 半波损失讨论

2.1 菲涅尔公式

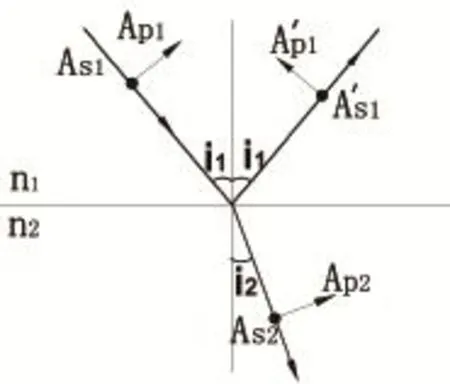
图1 光矢量的正向规定[21]

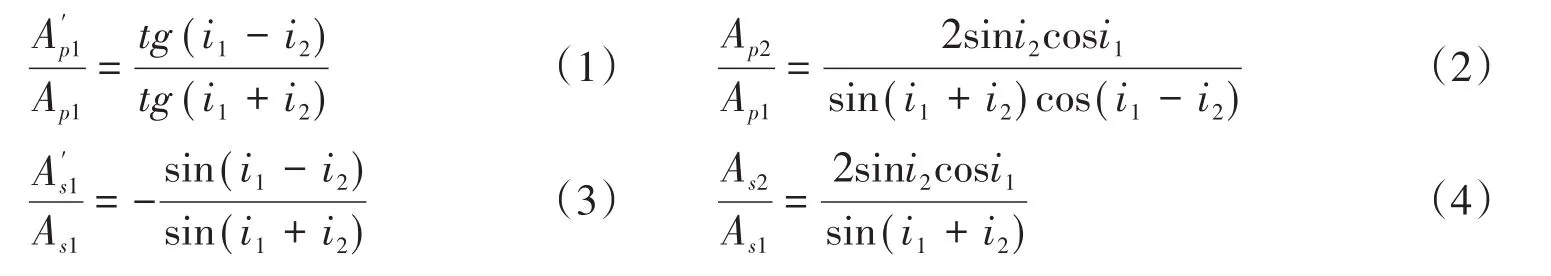
2.2 光矢量方向变化规律

用ic表示全反射临界角。i1＞ic时发生全反射,其相位改变较为复杂，不作阐述。

用ib表示布儒斯特角，当入射角i1=ib时，由布儒斯特定律可知反射光中无平行矢量P光。此时入射角与折射角之和为900，即ib+i2=900。所以只要考虑入射角i1＞ib或者i1＜ib时的情况。由折射定律n1sini1=n2sini2推算可以得到以下结论：

①当i1＞ib时，入射角i1增大时，折射角i2也增大，i1+i2＞ 900。

②当i1＜ib时，入射角i1减小时，折射角i2也减小，i1+i2＜ 900。

一般情况下，随着介质分布与入射角的不同，由（1）—（4）式可推得反射光、折射光的分量相对入射光规定的正方向变化如表1。

2.3 半波损失存在条件

根据半波损失的定义，由表1中列出不同条件下反射、折射过程中光矢量的方向变化情况可以得出以下结论：

①折射光与入射光之间不存在半波损失。

②只有界面上反射光的S分量与P分量相对于入射光的S分量与P分量方向均反向，才存在半波损失。

③外反射（n1＜n2）时，反射光相对入射光有可能存在半波损失。判断方法：根据入射角情况，从表1中确定反射光波S分量与P分量与规定的正方是否存在反转情况，从而确定光矢量的实际方向，再与入射光比对，反射光的S分量与P分量相对于入射光的S分量与P分量方向均反转，就存在半波损失。

表1 光在反射、折射过程中光矢量各分量方向变化情况

2.4 不同入射角时半波损失讨论

2.4.1 正入射（i1≈0）

当n1＜n2，i1＜ib时，比对图1反射光矢量规定的正方向如图2（a）虚线所示，从表1中查得对应规定的正方向反射光的S矢量反向，P矢量同向，调整虚线中S矢量方向以后如图2（a）右端实线所示，反射光与入射光对应分量的方向相反，那么合矢量E是反转的，发生了半波损失。不难分析，内反射情况下无半波损失（如图2（b）所示）。

图2 正入射各振幅矢量图

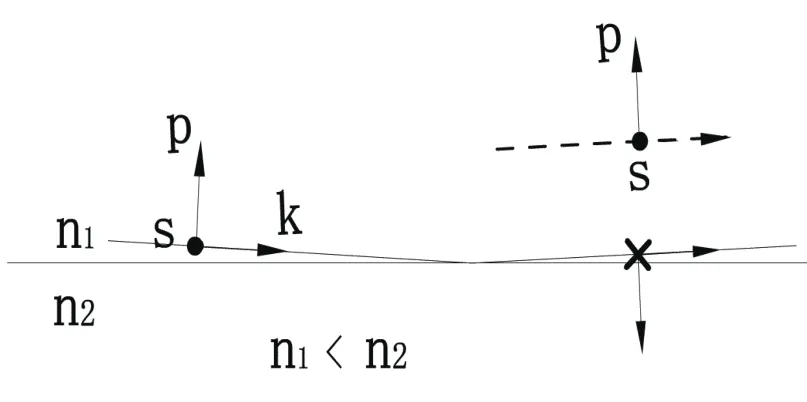
图3 掠入射各振幅矢量

掠入射满足n1＜n2、i1＞i2、i1＞ib，查表可知反射光矢量的S分量、P分量与规定的正方向（图3虚线所示）均相反，实际方向如图3右下端所示。反射光的S分量与入射光的S分量方向相反，其对应的P分量也几乎反向，则E矢量反转，有半波损失。

2.4.3 斜入射

斜入射时，经分析如图4所示。外反射时，反射光与入射光的S分量的方向反向，P分量成一角度。内反射时，反射光与入射光的S分量同向，P分量互成一角度。所以，斜入射的时候，反射光相对于入射光而言，光矢量E不存在方向反向，无半波损失。

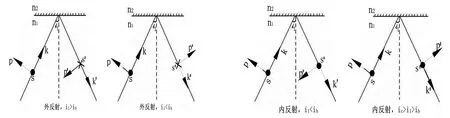
图4 斜入射各振幅矢量图

3 薄膜干涉中的附加光程差讨论

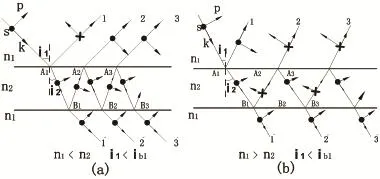
图5 均匀介质中各振幅矢量图

3.1 薄膜置于均匀介质中

3.1.1 当n1＜n2＞n1时

当入射角i1＜ib1时，查表可知上界面反射光1的S分量反向、P分量同向。在i1＜ib1的条件下，可以证明i2＜ib2，光束A1B1在下界面反射时属于内反射，S分量同向、P分量反向，光束B1A2穿出上界面时S分量、P分量均不反转，见图5（a）光束2。依此类推可以得出各光束中E矢量的S分量、P分量的实际方向如图5（a）所示。可见，图5（a）中1、2两束反射光的S分量反向、P分量也反向，存在λ 2附加程差，但是上下两个反射界面处没有半波损失。所以半波损失与附加光程差之间没有必然的因果关系。但是，正入射的时候,图5（a）中薄膜上表面反射的光束1对应它的入射光有半波损失存在。

还可类似分析n2＞ n1且i1＞ib时S、P分量方向。

3.1.2 当n1＞n2＜n1时

当n1＞ n2、i1＜ib1时S、P分量方向如图5（b）所示。可见，图5（b）中光束1、光束2的S分量方向反向，它们的P分量方向也反向，二者之间存在附加光程差λ 2，但因为是斜入射，反射界面处反射光相对入射光没有半波损失。但在正入射（i1≈0）时,根据前述分析可知5（b）下表面反射光束相对入射光存在半波损失。还可类似分析n1＞ n2且ic＞i1＞ib的情况。

3.2 薄膜置于上下折射率不同的介质中

3.2.1 n1＜n2＜n3或n1＞n2＞n3

当n1＜n2＜n3或n1＞n2＞n3时，上、下界面均为内反射或外反射，反射的物理性质相同。图6是以n1＜n2＜n3为例分析的结果，1、2两束光的S分量方向相同，无论P分量怎样改变方向，两反射光振动合矢量方向不会相反，不存在π附加相位差，也就无λ 2附加光程差。

如果是正入射（i1≈0）,图6中（a）上、下表面反射光束相对入射光存在半波损失。

图6 n1＜n2＜n3非均匀介质中各振幅矢量图

3.2.2n1＜n2＞n3或n1＞n2＜n3

当n1＜n2＞n3或n1＞ n2＜n3时，薄膜所在上、下界面反射的物理性质刚好相反，且布儒斯特角大小不一样，情况较为复杂。

以n1＜n2＞n3为例分析，

我们发现上、下界面反射的物理性质相反时，大多数情况1、2两束光有λ 2附加光程差，但也存在一定范围内的入射角使得反射光之间附加光程差不为λ 2。

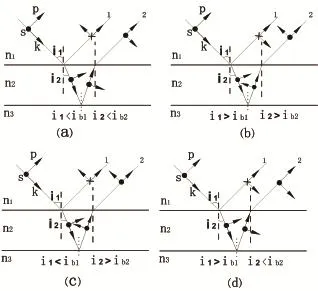
图7 n1＜n2＞n3非均匀介质中各振幅矢量图

如果是正入射（i1≈0）,由折射定律知i2≈0，两入射角均应小于布儒斯特角。图7（a）中1、2两束光有λ 2的附加程差，反射光束1相对入射光而言存在半波损失。

4 半波损失与附加光程差二者的关系

半波损失是指反射光与入射光两者之间的关系，如果界面上反射光的E矢量与入射光的E矢量方向相反，等效于反射光与入射光产生了π相位突变或者λ 2光程（不是光程差）突变。

薄膜干涉中的附加光程差指两束反射光之间的关系。产生λ 2额外光程差的本质是两反射光光振动的合矢量方向相反，产生了π相位突变所致。

所以，按照文献对半波损失、薄膜干涉中的额外光程差的概念界定，两者之间没有必然的因果关系。在前述讨论中，薄膜干涉中斜入射时反射光1、2之间存在有λ 2附加光程差，而上、下反射面处并不存在半波损失的情况。

5 结论

由以上讨论可以得出如下结论：

5.1 关于半波损失

①半波损失需满足三个条件：光疏介质到光密介质、掠入射或者正入射、反射。

②光在折射时不存在半波损失。

③光斜入射时不存在半波损失。

④可以把半波损失表述为：当光以正入射或掠入射的角度从光疏介质射向光密介质时，反射光的光矢量与其入射光的光矢量方向相反，发生π相位突变，相当于λ 2的光程突变。

5.2 关于薄膜干涉中的附加光程差

①薄膜置于均匀介质（n1＜n2＞n1或者n1＞n2＜n1）中，反射光束1、2存在附加光程差为λ 2。

②薄膜置于上下折射率不同的介质中。当n1＜n2＜n3或n1＞n2＞n3时，反射光束1、2之间没有λ 2附加光程差；在n1＜n2＞n3或n1＞n2＜n3的情况下，反射光束1、2间一般存在λ 2附加程差。

③在牛顿环等薄膜干涉实例中，一般采用正入射，当n1＜n2＞n1或n1＞n2＜n1或n1＜n2＞n3或n1＞n2＜n3时，反射光束1、2均存在附加光程差λ 2，上、下反射界面处有一处存在半波损失；满足n1＜n2＜n3或n1＞n2＞n3时，反射光束1与反射光束2之间没有λ 2附加光程差，其中n1＜n2＜n3时上、下表面反射光束相对入射光均存在半波损失。这可能就是一般文献上把λ 2附加光程差归因于半波损失的原因所在，其实二者之间并没有一定的因果关系。

④“附加光程差”可以采用虞福春先生的定义[24]：由于光在两个界面的反射的物理性质不同，两束相干的反射光的光矢量E的振动方向相反，就存在一个附加的半波程差。在大学物理教学中，讲解分振幅薄膜干涉时，因为课时的关系不必去做上述这样的详细分析，考虑到牛顿环、劈尖、增透射膜等实际应用一般都是采取正入射，所以重点讲解正入射这种特例如何判断附加光程差即可。