分形布朗运动驱动下幂期权的保险精算法

祝丽萍 崔朝剑雄 张 胜 罗梦迪

（昌吉学院数学系 新疆 昌吉 831100）

1 引言

幂期权是金融市场中一类变异期权,区别于一般期权的特点在于，其持有人在到期日行权条件不是简单地用标的资产的价格与执行价格相比较,而是用标的资产的某个指数幂与执行价格相对比,因而幂期权能够放大风险,且具有一定的灵活性,能满足不同风险偏好的投资者的需要[1]。为了简化，传统的金融产品定价理论往往假设金融市场是无套利、均衡和完备的市场,然后就可以得到相应的定价公式[2]。然而实际市场总是有套利、非均衡、不完备的,因而传统的期权定价模型往往不太适合真实市场。注意到保险产品和期权在性质上的类似，1998年,Bladt和Rydberg首次将保险精算方法运用在期权定价中,称为保险期权定价法[3]，该方法对金融市场并没有特别的假设,适应性也比较广泛。但是，2005年Schmitz用反例说明Bladt和Rydberg基本结论是错误的,关键就是Bladt和Rydberg的行权条件会导致套利机会[4]。2008年,郑红等人在利用保险精算方法上进一步修正了Bladt和Rydberg的精算公式，得到新的欧式期权保险精算定价公式[5]。其次,传统的模型往往都是基于正态分布的模型假设,但实际数据往往都具有尖峰厚尾的特点，与正态分布有差异。分形布朗运动可以描述这种非正态的特性,于是1997年Roger将分形布朗运动引入期权定价公式[6]。由于现存的文献中基于分形布朗运动用保险精算定价法研究幂期权还不多,因此本文试图讨论保险精算方法在股票价格服从分形布朗运动条件下幂期权定价问题中,导出其定价公式,进一步推广郑红等人的成果。

2 幂期权的保险精算定价模型

由于幂期权也分为看涨和看跌两种。本文以看涨幂期权为例来研究。

假定金融市场由两种资产来组成，一种是无风险资产，另一种是风险资产（例如股票）。假设在t时刻，无风险资产瞬时收益率为r(t),其价格过程为Q(t):t≥0,风险资产的价格过程为S(t):t≥0，是定义在给出的滤子化完备概率空间(Q ,F,F(t)t≥0,P)上的随机过程,F(t):t≥0是由S(t)所产生的自然滤子，讨论时间区间为[0,T],0表示为初始时刻,T表示为到期日，假设S(0)=S为大于零的常数。

定义1假设S(t):t≥0是某个随机的过程,S(0)=S,β(t):t≥0是某一函数。如果在区间[0 ,t]上有

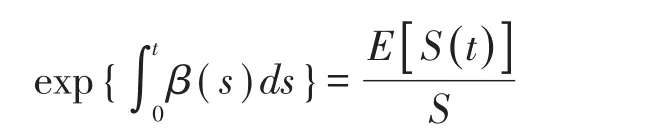
假设C(K,T)表示以股票的价格S(t)作为标的资产,执行价格为K,到期日为T的看涨幂期权的保险精算定价。

定义2称当期权在到期日被执行时，股票在到期日股价S(T)α折现值与其执行价K之间的差额在股票价格实际分布下的数学期望为分形布朗运动驱动下幂期权保险精算的价值。一般情况下无风险资产按照无风险利率折现，而风险资产按其期望收益率折现，即

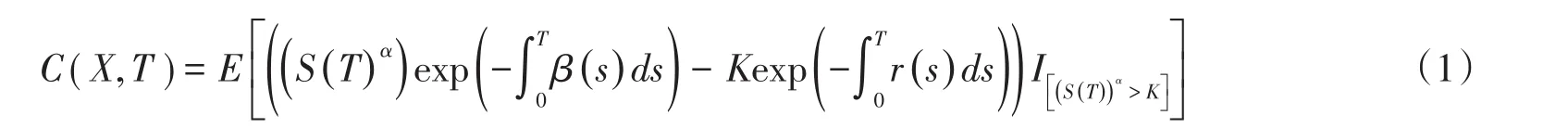
其中,E表示T时刻实际概率测度下的数学期望。

相比于传统期权保险精算定价法，此精算定价法严格按照期权的定义和保险精算的思想来给出期权的定价模型。最关键的区别是期权所执行的条件,即上式中的示性函数。

3 幂期权的精算定价公式

为求解公式（1）,我们进一步假设股票的飘移项和波动项以及利率都是常值，并且假设股票价格服从分形布朗运动。

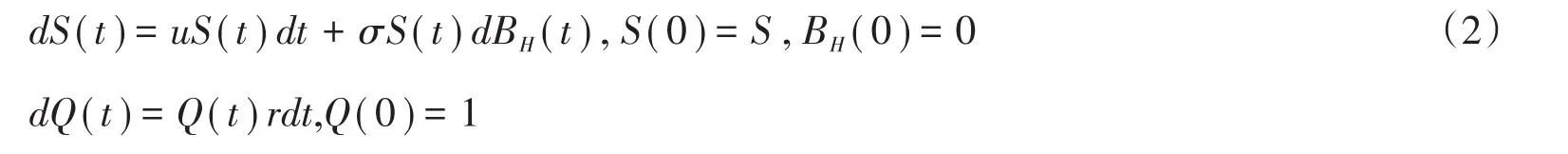
其中，H:0≤H≤1是赫斯特指数,BH()t代表参数为H的分形布朗运动.u,σ,r都是常数。下面仅给出看涨幂期权在分形布朗运动驱动下的保险精算定价公式。

因为分形布朗运动不再是半鞅,故不能用Itô引理来求解，就需要以下得引理

引理1[7]对于0≤t≤T随机微分方程（2）的解是

定理1在基本的假设下,分形布朗运动驱动下幂期权的保险精算定价公式应为

其中，

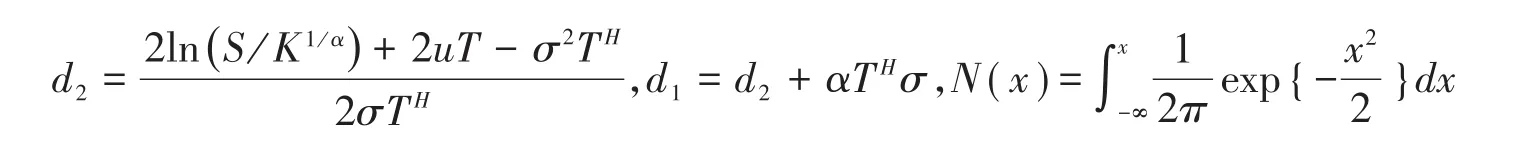
证明：由引理1,

特别地有,

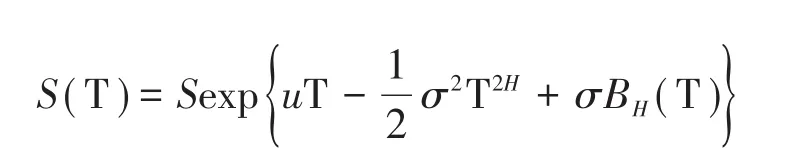
注意到σBH(t)～N( )0,σ2T2H,从而有

注意到,定义2中执行期权的条件S(T)α＞K的等价条件是：

现将式（5）（6）带入式（1）即得公式（4）。证毕。

4 结论

从公式（4）我们可以看出,在风险为中性的条件下,公式（4）与何成洁等和周圣武文等文中通过风险中性原理推导的结果一致[8,9],而且与唐奎等人研究的结论一致,并且我们在唐奎等人文章证明过程中发现其结论只能在风险中性情况下才成立【10】,这一点说明我们方法的优势。当α=1时,幂期权就转变为一般期权,结论与郑红文中的结果一致。因此，本文的确是上述文章的推广。但是由于我们的研究仅仅是在漂移项、波动项都为常数，也不带分红的情况下进行的，具有一定的局限性，今后我们要对幂期权在具有时间依赖的漂移项、波动项和利率以及带有红利分配的保险精算定价问题进一步讨论。