机械臂拾取装置的模糊控制仿真研究

梁开旭

(长安大学工程机械学院，陕西西安710064)

0 引言

在当今制造业中，微电子技术、传感器技术等飞速发展，在提高生产效率的同时也需保障产品的质量，自动化越来越受到企业的重视。工业机械臂作为自动化生产线上的重要部分，将机械化和自动化有机的结合在一起，大大提高了生产自动化、精准化[1]。机械臂拾取装置在电子制造领域较为普遍，为了实现加快生产效率和保证产品质量的目标，机械臂拾取装置在工作过程中需具备快速准确定位的性能。模糊控制是以模糊集理论、模糊语言变量和模糊逻辑推理为基础的一种智能算法，在工业生产领域的控制上有着广泛的应用[2]。针对机械臂拾取装置的控制性能，应用模糊控制方法对其进行仿真研究，实现快速拾取和准确定位。

1 模糊控制基本原理

模糊控制理论是一种非线性智能控制方法，以模糊集合理论、模糊语言变量及模糊逻辑推理为基础，它将模糊数学很好地与控制系统相结合并得以应用[3]。一般用于不需要建立严谨的数学模型的系统，可利用人的经验和知识来很好地控制。该方法是根据控制系统的特点和控制系统的反馈信号与参数输入比较，计算得到误差信号，再将误差信号进行模糊化处理为对应的模糊量，然后根据专家经验和被控系统特点编制模糊控制规则，将信号的模糊量用模糊语言集合的一个模糊向量表示，结合模糊规则进行模糊决策和推理，最后将模糊控制器的输出量作为系统的输入信号加载到被控对象上进行控制。其基本原理如图1[4]。

图1 模糊控制原理框图

模糊控制器的设计是模糊控制方法的应用重点，模糊控制系统的性能主要取决于模糊控制器的结构、所制定的模糊规则、推理算法及模糊决策的方法等因素[3]。具体的设计结合机械臂拾取系统进行详细说明。

2 机械臂拾取装置的建模仿真

2.1 机械臂拾取装置建模

图2 机械臂拾取装置

机械臂拾取装置常应用于电子集成芯片的生产线上，利用其将电子芯片和零件放置到电路板上的指定位置，完成安装和焊接。如图2所示为机械臂拾取装置的简图，通过机械臂内部输入气体，利用弹簧的压缩驱使机械臂运动，完成拾取工作。假设系统输入气体压力为P、机械臂质量M=0.082 kg、元件质量m=0.023 kg、弹簧刚度k=3.8 N/m、阻尼系数c=0.04 N/(m·s-1)、活塞作用面积A=0.002 m2。

设输出位移为x，对系统进行受力分析，列出系统的动力学方程：

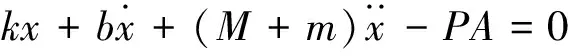
(1)

对上式代入数据并进行拉普拉斯变换，得到系统的闭环传递函数[5]：

(2)

二阶系统的闭环传递函数的标准形式为：

(3)

由此得到系统的特征方程：

(4)

由式(4)可解得系统的固有频率和阻尼比分别为ωn=6.3245 rad/s，ζ=0.0316，用这两个参数经计算得到系统的调节时间和超调量：

(5)

由此可以看出机械臂拾取系统在工作过程中调节时间过长导致效率很低，超调量过大导致定位不准振动严重。因此我们应用模糊控制方法来进行控制，以优化系统性能指标。

2.2 机械臂拾取装置仿真

针对此机械臂拾取系统建立模糊闭环控制系统，其控制最终的效果是通过调整输入机械臂气体压力的大小，将拾取的电子元件准确地放置在指定的位置点。系统控制信号选择机械臂末端位移的测量信号，然后根据位移测量值与参考值的偏差e及偏差变化率ec来控制输入压力P的大小，从而控制机械臂拾取元件到达指定位置。在此系统中的模糊控制器的输入量是机械臂位移的偏差e和偏差变化率ec，输出量u是输入气体的压力。假设机械臂拾取元件的运动位移为500 mm，最大超调量不超过10%。

位移偏差e的论域为选用[-0.5，0.5]，定义模糊集为{NZP}，模糊集里的字母N、Z、P分别表示参考位移和系统输出位移的偏差为负、偏差为零，偏差为正。位移偏差变化率ec的论域定为[-1，1]，定义模糊集也同样为{NZP}，模糊集里的字母N、Z、P分别表示机械臂位移偏差变化率为负、位移偏差变化率为零，位移偏差变化率为正。模糊控制器输入变量(位移偏差和偏差变化率)的隶属度函数均选高斯函数。压力P的论域为[0，10]，定义模糊集为{P1P2P3P4P5}，表示压力依次增大，模糊控制器输出量(压力)的隶属度函数选用三角形函数。

模糊控制器的控制规则没有特定必须遵循的原理，它是结合人们学习，试验和长期经验积累而确定的，不同的控制者会有不同的控制规则，但只要规则编制合理都可以达到想要的控制效果。经对机械臂拾取装置的综合分析以及实际生活的经验，就此系统运用and逻辑关系编制的模糊控制规则如表1。

表1 拾取系统模糊控制规则表

在Matlab/Simulink中建立基于模糊控制器的机械臂拾取系统的仿真模型如图3，图4为机械臂拾取系统模型。

图3 基于模糊控制的机械臂拾取系统仿真模型

图4 机械臂拾取系统模型

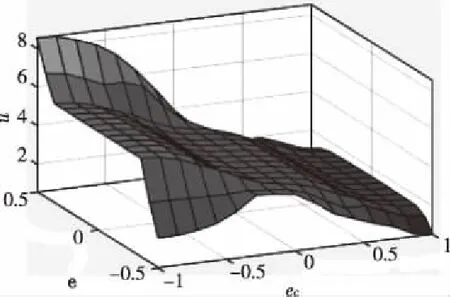
图5 模糊推理输入输出曲面视图

在Matlab中调用其模糊逻辑工具箱，根据之前的分析和控制策略设计机械臂拾取系统的模糊控制器[6]。设计流程为：在Matlab命令窗口输入fuzzy调出模糊逻辑控制器，建立模糊控制器的输入输出量和控制规则之间的逻辑关系，确定各自适用的隶属度函数以及之前确定的各个变量所对应的论域，根据模糊规则表输入模糊控制规则，完成模糊控制器的设计。最终得到能够全面反映控制器输入位移偏差和位移偏差变化率以及输出压力之间关系的三维曲面视图如图5，所得到的三维曲面显示越光滑平整其系统的控制效果会越好。

将模糊控制器导入上述机械臂拾取仿真模型中进行运行仿真，在示波器中得到机械臂拾取系统工作过程的仿真曲线，图6为系统位移—时间曲线，图7为系统压力—时间曲线。

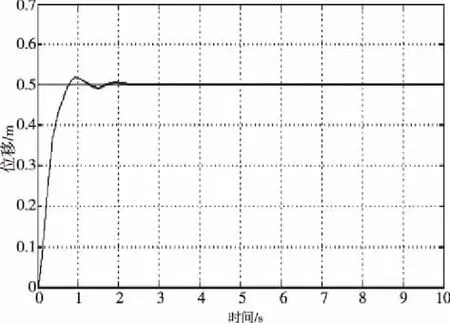
图6 位移—时间仿真曲线

图7 压力—时间仿真曲线

3 结论

针对机械臂电子拾取装置运用模糊控制法进行工作控制仿真，通过分析仿真曲线图6可以看出，对系统运用模糊控制之后系统超调量为4%，相对而言非常小了，并且系统运行过程中在约2.3 s就已经调节就位，系统的调节时间大大减小，这就使得机械臂拾取系统既保证了工作的稳定性又提高了生产效率，说明模糊控制在此系统中的控制效果是比较理想的。系统控制性能的好坏，主要在于模糊控制器各参数的论域、模糊规则及模糊推理的合理性，只要参数的论域、模糊规则确定合理，系统的控制性能完全可以达到更好的效果。