7050-T7451铝合金薄壁件铣削仿真建模及试验分析

纪合溪，葛茂杰，于 健，姜 楠，孙卫峰

(1.福建众人机械制造有限公司，福建宁德352000；2.烟台龙源电力技术股份有限公司，山东烟台264006)

0 引言

铝合金的特点是重量轻、刚度好、强度高、耐腐蚀、平整性好，易于制造复杂形态的表面，因此铝合金在汽车、航空、航天、轮船等工业生产中广泛应用。但是，由于薄壁铝合金部件结构复杂，刚性非常低，切削加工时的切削力容易产生较大的铣削余量，造成较差的加工工艺，导致加工变形或颤振。

目前，国内外铝合金薄壁件的理论模型中，Altinas等[1]在考虑轴向、切向、径向切削力对切削系统稳定性的基础上，建立相关动力学模型。GonZalo等[2]以切削最优、提高工件表面精度为目的，利用有限元手段，模拟铝合金薄壁结构件的铣削过程，以获得不同阶段的切削动态特性。浙江大学董辉跃等[3-4]则通过用有限元手段，研究装夹对薄壁工件切削加工系统的影响。

本文针对铝合金7050-T7451薄壁零件加工变形为研究背景，建立铝合金薄壁件铣削动力学模型，并进一步建立有限元仿真分析模型，揭示微切削区域塑性变形及切削力变化规律，并进行试验验证。

1 铣削建模关键技术

1.1 铣削动力学模型

铣削动力学模型是建立在刀具和工件刚度的切削稳定性模型，如图1所示。

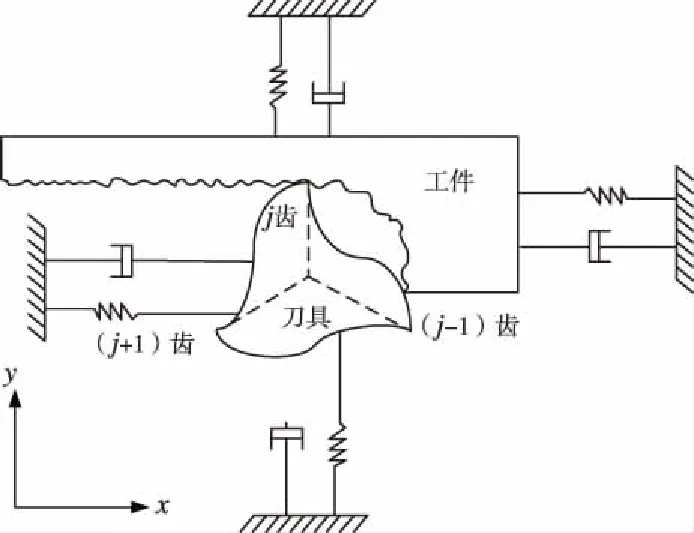
图1 铣削动力学模型

将铣刀简化为N个齿，x和y方向两个自由度，薄壁铣削的动力学方程可以得到：

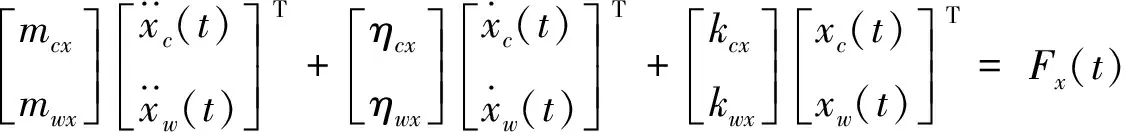
(1)

式中：mcx、ηcx、kcx、mcy、ηcy、kcy和mwx、ηwx、kwx、mwy、ηwy、kwy为铣刀和工件在x与y方向的模态、阻尼和刚度特性。总切削力F(t)在x与y方向上的分力可用Fx(t)、Fy(t)表达。

1.2 动态切屑厚度

第j切削刃切削时切屑的动态厚度h(φj)可以通过当前刀齿切削时和前一个刀具切削时的位移差计算获得，如式(2)：

h(φj)=[Δxsinφj+Δycosφj]g(φj)

(2)

式中：φj是刀齿j的瞬时接触角，φj=(j-1)φp+ωt，φp是铣刀的齿间角，φp=2π/N。

1.3 动态切削力

刀具第j齿上的切向力(Ftj)和径向力(Frj)与切深(ap)及切削厚度(h)成正比：

Ftj=Ktaph(φj)，Frj=KrFtj

(3)

式中：切削力系数Kt和Kr为常数。通过在x和y方向对切削力进行分解，并将所有的切削力单元相加，按矩阵形式表示可得：

(4)

(5)

式(5)中：αxx，αxy，αyx，αyy为时变的动态铣削力系数，且

考虑时间和角速度的变化，因此方程(5)可以表达为时域的矩阵：

(6)

2 有限元模拟

2.1 工件材料的本构模型

采用Johnson-Cook剪切失效(shear failure)模型[5]，其表达式为：

(7)

(8)

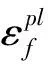
2.2 刀屑摩擦模型

采用库仑摩擦模型[6]，在粘着摩擦区内，定义此区域内的摩擦应力为固定值，其数值为等于或略高于极限剪切应力τmax；在滑动摩擦区内，定义此区域的摩擦应力符合库仑摩擦定律，与正应力成正比。其关系如下：

τf=μσn当τf<τmax(滑移摩擦区)

τf=τmax当τf≥τmax(粘结摩擦区)

其中，τf为摩擦剪应力；τmax为材料的最大剪应力；σn为正应力；μ为摩擦系数，取常规值0.1。

2.3 几何模型及网格划分

铝合金薄壁工件网格为C3D8RT类型，刀具网格为C3D4T类型，采用通用显式动力分析步(Dynamic，Explicit)，边界条件见图2，对工件约束Y、Z方向的移动自由度U2、U3及三个方向的旋转自由度UR1、UR2、UR3，并施加X方向的进给速度vf=20 mm/min，刀具的旋转速度n=10000 r/min施加在刀具的参考点RP上，如图3。

2.4 应力和应变的分布规律

图4和图5为刀具铣削过程中的流动应力、等效塑性应变分布云图，表1为铣削过程中各点的流动应力和等效塑性应变数值。在刀具与工件刚开始接触时，最大应力主要集中在刀屑接触区。对比铣削过程切屑和工件中各处的应力和应变，发现工件的流动应力和等效塑性应变数值明显低于切屑，而且工件的应力应变值变化不明显。

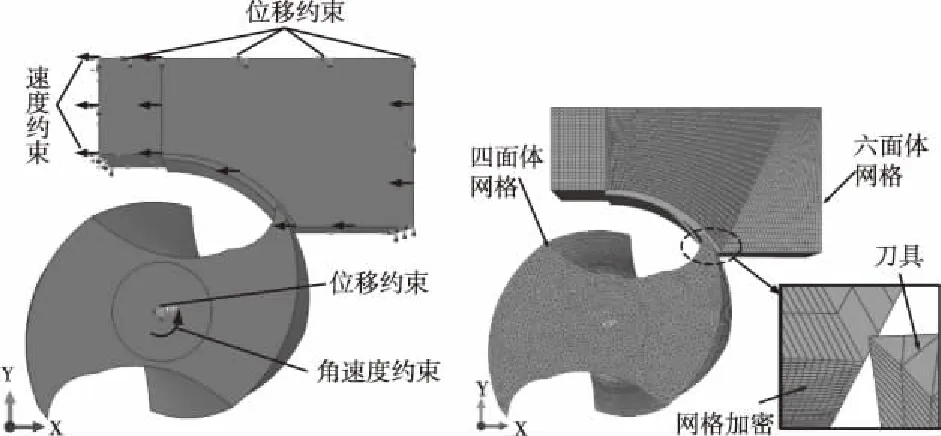
图2 模型的边界条件 图3 模型的网格划分

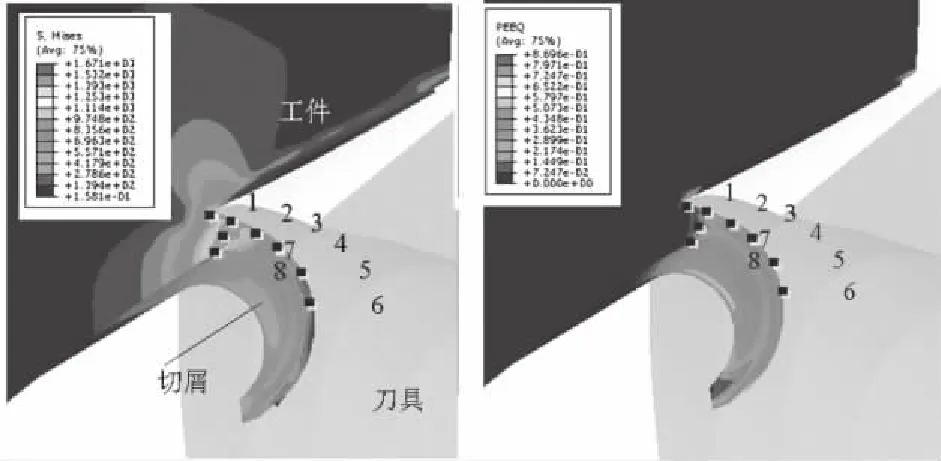
图4 铣削过程中流动应力 图5 铣削过程中等效塑性应变

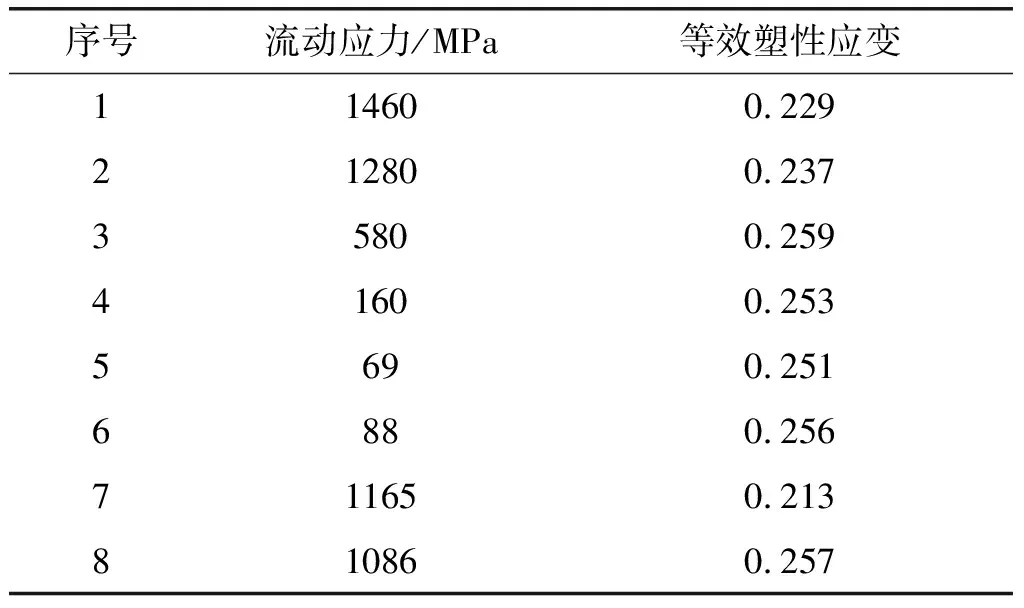
表1 铣削过程中各点应力应变数值

3 铣削试验

3.1 试验工件

本试验采用铝合金7050-T7451板材，工件为30 mm(高度H)×100 mm(长度L)×10 mm(厚度h)，铣刀对工件侧壁进行铣削，见图6。

3.2 刀具参数

铣刀的相关几何参数如表2。

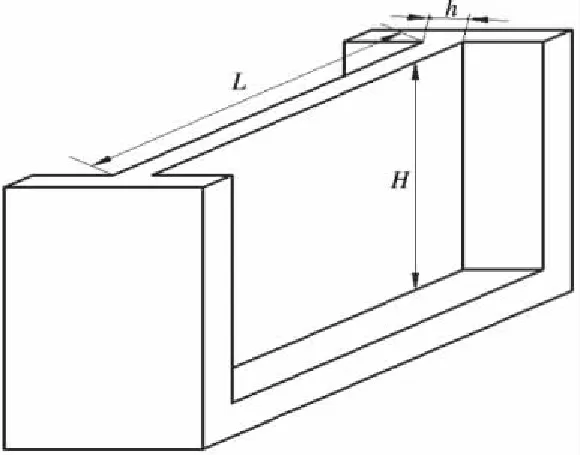
图6 铣削工件示意图

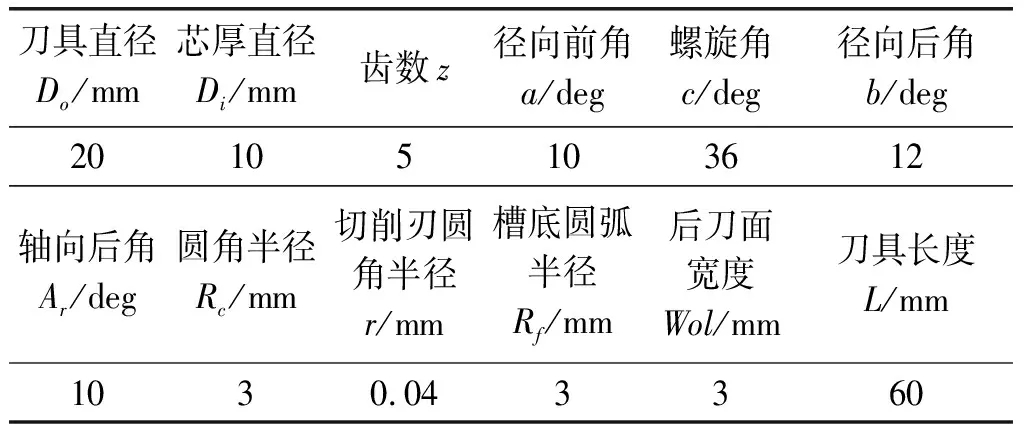
表2刀具的几何信息表

3.3 试验设备

机床采用DMG DMC 635V数控加工中心，利用YDCB-III05高频响三维动态测力仪，通过YE5850动态应变放大器，由PCI-9118数据采集装置进行数据采集。试验设备的连接情况如图7。

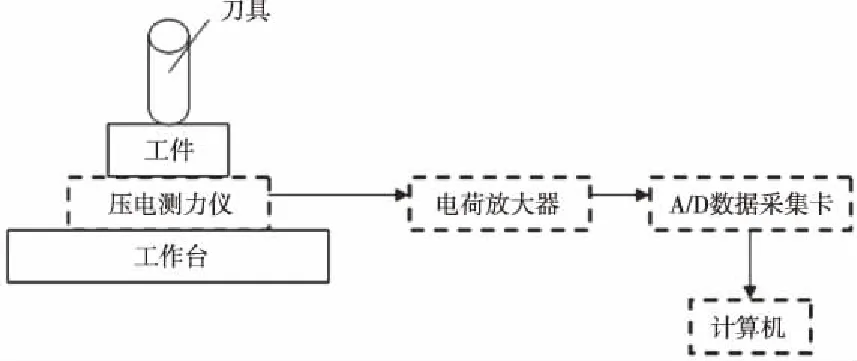
图7 切削力测试系统组成图

通过铣削实验，对比模拟值和实验值，见表3，由表3可知，Fx的平均误差为11.96%，y向平均误差为10.72%，z向平均误差为21.36%，合力平均误差为10.18%，除z向外，各向误差值均小于10%，说明预测的值同实验获得的值吻合度高。故此，本文所建立的航空钛合金材料铣削力模型在当前的加工设备下是适用的，尤其所预测的各向铣削力理论值是可靠的。虽然该理论模型是针对具体材料的，但它对其它同类材料而言也是可信的，只需要增加一个修正阐述即可。所以，本研究是具有工程意义的。

表3 理论值与实际测量值的比较

4 结论

1)针对铝合金7050-T7451薄壁零件，建立铝合金薄壁件铣削动力学模型和有限元铣削模型。

2)通过仿真得到了X、Y、Z方向的切削力，通过铣削加工试验，获取铣削力数值并与仿真铣削力进行对比，验证了试验模型的准确性。为后续试验研究(加工效果，加工质量等)做好准备。