球杆系统建模及其闭环控制器的设计

刘诗宇

(西北工业大学机电学院，陕西西安710068)

0 引言

在现代控制理论中，球杆系统是一个经典的控制系统研究对象(图1)，由于其非线性特性及开环系统的不稳定性，球杆系统实验装置可应用于控制理论及方法的研究[1]。对于球杆系统的建模过程以及闭环系统控制器的设计，仍有着许多可研究的角度和方法。

文献[2]提出了基于牛顿力学法和基于拉格朗日法的建模过程，并讨论了PID控制器的设计过程；文献[3]对系统微分方程在平衡位置点上进行线性化处理，通过极点配置法设计了状态反馈矩阵。这两种控制器的设计方法均较为随机，例如PID控制主要依靠调节比例控制Kp、积分控制Ki和微分控制Kd这三个参数来决定控制器的性能，其实际值仅通过调试的方法进行选取，过程较为繁琐；而通过极点配置法设计控制器，也仅需将极点配置在复数域的负半平面，以使得闭环系统稳定，而对于实际极点的选择也较为随机，选取不恰当的极点会影响闭环系统的特性。文献[4]、[5]分别提出了最优鲁棒控制器和基于遗传算法的线性二次型控制方法，但文献中提出的模型都经过了明显简化，仿真结果和实际情况会有一定差异。文献[6]提出了基于LQR的最优控制器设计，该线性控制器的设计方法具有较强的实际意义，然而文献中对于球杆系统建模及LQR最优控制中权重矩阵Q、R的研究均过于简化。

图1 球杆系统实验平台

本文针对球杆系统的研究现状，基于拉格朗日法重新建立了球杆系统的全量模型，并通过基于线性二次型(LQR)的最优控制，设计了系统状态反馈控制器。此设计过程即选取负反馈矩阵Kopt的值，使得闭环系统在内部稳定的前提下，对系统的动势能及驱动器的电能消耗进行优化。另外，本文在状态反馈控制器的基础上，提出了轨迹追踪器的设计方法，并在Matlab-Simulink仿真环境下验证了该控制器设计方法的有效性。

1 球杆系统建模

1.1 基于拉格朗日法的建模过程

图2 球杆系统简图

经典的球杆系统实验平台是由导轨、钢球、皮带、传动轮、伺服电机和电源等组成，其系统简图如图2。导轨中心固定，两端与皮带相连，伺服电机由带传动方式将驱动轴的转动角转化为导轨的俯仰角变化。导轨旋转中心设置有角度传感器，测量导轨的倾斜角度。导轨上方安装摄像头，以测量小球在导轨上的位置。

为便于研究计算，本文将按表1所示的命名规则对系统各部件参数及变量进行表示。

根据文献[6]，球杆系统的数学模型可通过拉格朗日方程描述。其优势在于通过求解系统的总动能和总势能即可求出系统微分方程，无需对系统各子部分进行建模。为得出系统总动能，首先对小球在导轨上的复合运动进行分析。

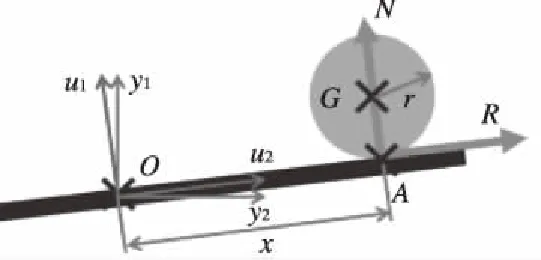
图3 小球运动及坐标系简图

表1 系统参数及变量表示

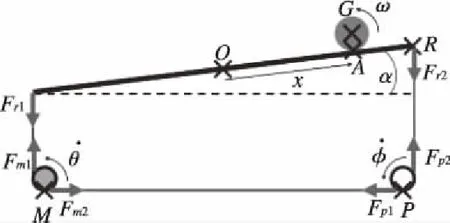
图4 球杆系统速度关系

对球杆系统整体做出合理假设如下：1)小球在导轨上作纯滚动运动，忽略小球和导轨之间的滑动及产生的摩擦；2)忽略带传动过程中的能量损失以及皮带的弹性性质所产生的位移和形变。则根据图4可得到以下关系：

系统总动能为：

系统总势能可表示为：

V=mg(xsin(α)+rcos(α))+cst

根据拉格朗日方法，构造拉格朗日因子。则系统运动模型可由拉格朗日微分方程描述：

其中：qi代表广义坐标，即为系统的主要研究变量x和α；Qi为广义力，可由虚功原理求解，可设：

其中：Qx=0，由于球杆系统在系统变量x上并未受到外力作用，小球在导轨上自由滚动。设δW为伺服电机做的虚功，则与电机驱动轴虚位移的关系有：

δW=Cmδθ

其中：Cm为电机输出力矩。

对直流伺服电机进行建模，直流伺服电机由伺服电压控制，其输入电压信号Uc、感应电动势e及输出力矩Cm分别可由下式表示。

Cm=kci

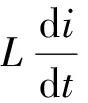
1.2 系统状态空间表示及其线性化

系统动力学微分方程可用矩阵形式表示：

为计算简便，可设：

J2=(Ib+mr2)

根据文献[7]所阐述的控制系统状态空间表示法，可设系统状态向量：

故可得到该非线性系统的状态空间表达式：

其中系统输入量为直流电机输入的电压信号：U=Uc。

由上式可知，系统状态x1e=xeq的平衡位置并未确定。即当导轨的俯仰角为0°时(导轨保持水平)，小球可以在导轨上任意位置保持平衡，电机通过带传动在导轨上施加的平衡力矩，使得小球保持静态平衡。在实际问题中，显然选取x1e=0(小球位于导轨正中心)，故Ue=0。

将得到的平衡位置点处的系统状态量代入，对非线性系统进行线性化，可最终得到线性系统的状态空间表达式：

其中：δX=X-Xe，δU=U-Ue，显然由于平衡位置点的选择，可将线性方程简化为：

即在平衡位置附近线性化得到的系统空间状态模型，可用于描述系统在任意位置的运动规律。

此处，矩阵A、B描述了系统的运动规律及控制规律，由线性化过程可得到：

而Y为系统输出向量，此处考虑系统为全状态量输出，以便于设计系统的状态反馈控制器。故可得到输出矩阵C和D的值：

2 基于LQR的状态反馈控制器设计

由文献[7-8]所阐述的状态反馈控制器的设计方法，以及采用基于线性二次型(LQR)的最优控制对控制器环节进行选取的过程，可设计状态负反馈调节输入量：

U=-KX+Uc

其中：Uc为系统外部输入量(此处为电机输入的电压信号)，K为待设计的状态反馈增益矩阵。则闭环系统可表示为：

Q为半正定的状态加权矩阵，R为正定的控制加权矩阵。根据文献[9]所阐述的基于二次型的最优控制设计方法可知，令二次型的性能指标J取极小值时，最优控制率可表示为：

Uopt=-R-1BTKX

其中：K为Reccati方程的常数解，该方程表示为：

KA+ATK-KBR-1BTK+Q=0

对于本文所研究的球杆系统，设计二次型性能指标函数J，以优化球杆系统运动过程中的动能、势能以及系统控制过程中所消耗的电能，并且考虑系统主要控制对象x、α的控制误差。系统内部的动能和势能可分别表示如下：

V=mg(xsin(α)+rcos(α))+cst≈(α→0)mgxα+cst

系统内部消耗的电能可表示为：

并且该控制系统主要目的是通过控制导轨俯仰角α从而控制小球在导轨上的位置x，故可针对系统状态量x和α设置偏差函数：

Je=x2+0.5α2

其中：S为XTU交叉项的加权矩阵。经过简单的矩阵转化，可将上式表示为：

R(U+R-1STX)]dt

可设U′=U+R-1STX，Q′=Q-SR-1ST。则可将上式转化为一般的二次型性能指标函数，且此时原线性系统表示为：

=(A-BR-1ST)X+BU′

根据一般形式下最优控制率的解，可得：

U′=-R-1BTKX

最终可得最优控制率为：

Uopt=U′-R-1STX=-R-1(BTK+ST)X

其中K为以下Reccati方程的常数解：

K(A-BR-1ST)+(A-BR-1ST)TK-KBR-1BTK+(Q-SR-1ST)=0

即对于闭环控制系统，最优控制下的状态反馈矩阵为：

Kopt=-R-1(BTK+ST)

对于权重矩阵Q、R、S的选取，根据前文对系统动势能、消耗电能以及系统状态量x和α偏差函数的建立，易求得：

3 轨迹追踪问题及设计方法

对于轨迹追踪问题，电机输入的电压信号不再作为闭环系统的输入量，而是将参考轨迹作为系统输入。对于本文研究的球杆系统，将系统状态量x，即小球在导轨上的位置作为参考输入。此时闭环系统反馈控制率可表示为：

U=-KX+GXd

其中：Xd即为系统外部输入的参考轨迹；G为待设计的补偿增益矩阵；K为状态反馈矩阵，可通过极点配置法或上文讨论的最优控制法求得，以使得闭环系统满足稳定性要求。则加入轨迹追踪环节的闭环控制系统可由下式和图5所示的系统框图表示。

图5 闭环系统框图

重新构造系统空间状态方程，加入外部参考状态量Xd，则未加入补偿增益矩阵G的开环系统可表示为：

其中：X仍为系统的状态向量，Xd=xd为针对小球在导轨上的位置x而输入的参考轨迹。则根据上文研究的球杆系统可知：A11=A，B1=B。且系统的参考轨迹输入并不会影响系统内部的运动规律，则有：

若此处Xd考虑为系统外部干扰，则矩阵A12可通过对扰动与系统运动产生的影响进行建模求得。并且，在本文研究内容中，由于参考输入仅为系统状态x需要追踪的一条轨迹，其本身并不需要运动方程描述，故A22=0。

可设系统仍为全状态量输出，且外部参考轨迹Xd并不需要输出。故有：

根据文献[7]中关于轨迹追踪器的设计方法，可知该线性系统方程可解，当且仅当存在Ta、Fa使得：

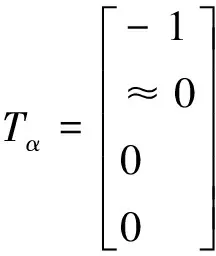
通过解得的Ta、Fa以及前文已设计的状态反馈矩阵Kopt，可求得系统追踪器的状态反馈控制率为：

U=-KoptX+(Fa-KoptTa)Xd

即闭环系统轨迹追踪的补偿增益矩阵：

G=Fa-KoptTa

4 仿真研究

4.1 状态反馈控制器仿真

下面通过在Matlab-Simulink环境下进行的数值仿真来验证上述的基于LQR的状态反馈控制器和轨迹追踪器设计方法的有效性。根据文献[10]提供的球杆系统实验平台各参数的实际数值，可得到系统空间状态表示的常数矩阵：

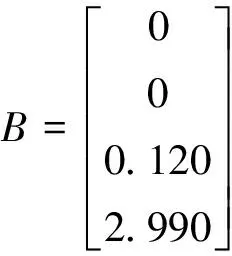
对于LQR最优控制中权重矩阵的选取，代入实际数值后可得：

R=0.385

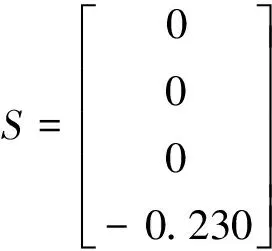
在实际问题中，闭环系统控制器性能主要考虑的指标是系统状态的稳定性以及对系统外部参考的追踪效果，而对系统消耗的能量要求并不严苛，故可增加LQR中对于系统状态权重矩阵Q的比重。在此研究实例中，可选取：Qs=500Q，Rs=R，Ss=S。并借助Matlab中Care函数(Continuous-time Algebraic Reccati Equation)，可求得闭环系统最优控制的状态反馈矩阵：

Kopt=[-36.634 75.635 -29.192 12.217]

对于轨迹追踪问题，将矩阵A11=A，B1=B中代入实际数值，可求得：

Fa=0.574

则补偿增益：G=Fa-KoptTa=-36.060。

在Simulink仿真环境下实现了闭环线性系统，并且关于反馈矩阵K的选取，对比了传统的极点配置法和基于LQR的最优控制法所设计的闭环系统性能。则对于仿真实验，给定系统输入的电压信号如图6。

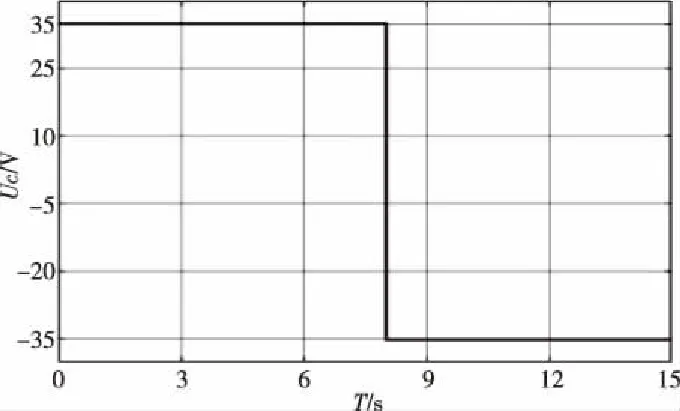
图6 闭环系统电压输入

根据文献[3]中提出的极点配置法，选取闭环系统A-BK的特征值：

则可得到状态反馈矩阵：

K=[-865.7 1718.1 -771.5 200.3]

将两种方法求得的反馈矩阵分别进行仿真实验，给定同样的电压输入信号，观察闭环系统对于小球在导轨上位置x的响应。

图7展示了对于两种方法求得的反馈矩阵K，闭环系统关于小球位置x相应的输出响应。可知两种设计方法得到的闭环系统均稳定，且响应时间均较短(1.5 s左右)。然而由于极点配置法求得的反馈增益的值较大，使得系统响应输出量较小，影响了系统对输入信号的敏感度，而降低K值的选取又会影响系统的稳定性。在对闭环系统A-BK极点的选取过程中，对于共轭复数根实际值的不同选取也会影响系统的震荡性。而根据LQR的最优控制所涉及的闭环系统控制器，显然在闭环系统稳定的前提下，系统响应时间较短，超调量较小，并且选取的反馈增益的值也更贴合实际(考虑了对系统能量及电机电能消耗的优化)，在实际问题中突显了其设计方法的优越性。

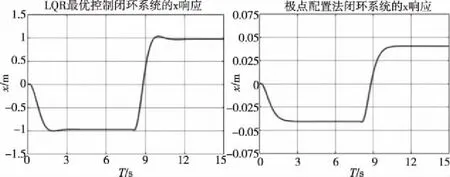
图7 小球位置输出响应

4.2 轨迹追踪器仿真

在Simulink仿真环境下，实现了对闭环系统轨迹追踪器的建模仿真，并给定外部输入的参考轨迹Xd如图8。

图8 小球位置x的参考轨迹输入

在仿真中，可得到闭环系统对于参考轨迹xd追踪的响应曲线以及球杆系统输入的控制电压U=-KX+GXd，分别由图9和图10表示。

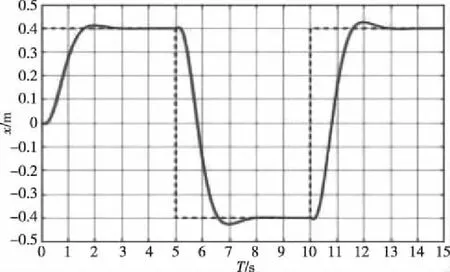
图9 小球位置x的响应曲线

由图9可得，闭环系统对轨迹追踪的响应时间约为2s，且稳态误差很小。且由图10可知，系统控制电压满足实验平台对输入电压的限制(最大电压不超过35V)，该闭环系统轨迹追踪器的设计得到验证。

图10 闭环控制系统输入电压

5 结论

本文在详细分析球杆系统基本原理的基础上，运用拉格朗日法建立了系统的全量数学模型，并对系统的非线性模型进行了线性化处理。针对线性化模型，研究了基于LQR的最优控制，设计了系统状态追踪器。并在Simulink仿真环境下实现了建模、仿真实验，对比研究了分别通过极点配置法和基于LQR的最优控制所得到的闭环系统控制器性能。利用极点配置法设计控制器具有操作简便的特点，但是对于所配置极点的选取具有一定的难度，其随机性会影响控制系统的性能。且此方法并未考虑实际情况，例如在实际问题中，若配置的极点过于远离复数域的原点，会使得控制器反馈增益矩阵K的值较大，导致控制器成本过高或系统消耗的能量过大。相反，基于LQR的最优控制可在满足闭环系统稳定的前提下，对设计的二次型性能指标函数进行优化，求得反馈增益矩阵的一个优化解。例如在本文所研究的球杆系统中，优化了系统动势能和电机驱动所消耗的电能，且文中探讨的设计过程有效地提出了权重矩阵Q、R和S的选取方法。显然该设计方法在实际问题中具有更大的优势。

本文在设计状态反馈控制器的基础之上，增加了轨迹追踪器环节，即讨论了补偿增益矩阵G的选取过程，使得系统状态量和参考轨迹输入量的误差趋近于零。最终通过Simulink仿真结果表明，本文设计的状态反馈控制器及轨迹追踪器达到了理想的设计效果。