全国名校椭圆拔高卷(B卷)答案与提示
2019-01-03 10:58徐利杰
中学生数理化(高中版.高二数学) 2018年12期
一、选择题
1.A 2.C 3.D 4.C 5.D 6.B 7.C 8.A 9.D 10.A 11.B 12.C 13.A 14.D 15.D 16.A 17.C 18.C 19.D 20.B 21.B 22.C 23.B 24.C 25.C 26.B 27.A 28.A 29.A 30.D 31.A 32.C
二、填空题
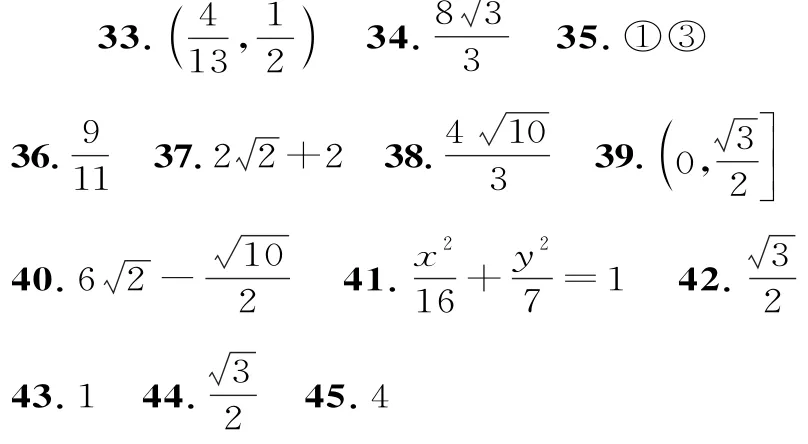
三、解答题


(2)当直线l的斜率为0时,令y=-1,则x=±4,此时以AB为直径的圆的方程为x2+(y+1)=16。
当直线l的斜率不存在时,以AB为直径的圆的方程为x2+y2=9。
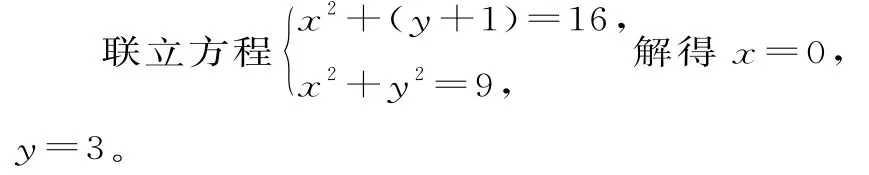
故两圆过点T(0,3)。
猜想以AB为直径的圆恒过定点T(0,3)。对一般情况,证明如下:

故存在以AB为直径的圆恒过定点T,且定点T的坐标为(0,3)。

(2)由题设知,l1:x=-2,l2:x=2。
切线l与椭圆C的方程联立消y得:
(1+4k2)x2+8kmx+4(m2-1)=0。①
因为l与C相切,所以①式的Δ=64k2m2-16(1+4k2)·(m2-1)=0,得m2-4k2=1。
l与l1,l2联立得M(-2,-2k+m),N(2,2k+m)。

49.(1)由题意知椭圆的长轴长2a=22,焦距2c=2。
又由椭圆的定义得|AF1|+|AF2|=2a,所以△AF1F2的周长为|AF1|+|AF2|+|F1F2|=2+2。
(2)由题意得l不垂直两坐标轴,故设l的方程为y=k(x+1)(k≠0)。

因为P,Q,R到x轴的距离依次成等比数列,所以|yP|·|yR|=|yQ|2。

(2)①由题设知直线斜率存在,设直线l方程为y=k(x+1),则P(0,k)。


51.(1)依题意,直线l显然不平行于坐标轴,故y=k(x+1)可化为
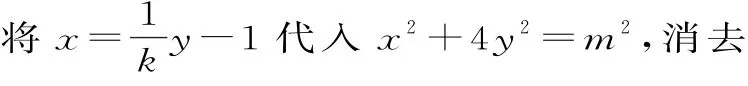

猜你喜欢
语数外学习·高中版上旬(2020年8期)2020-09-10
电脑爱好者(2018年12期)2018-06-26
福建中学数学(2016年7期)2016-12-03
中学生数理化·高二版(2016年7期)2016-05-14
数学教学通讯·初中版(2015年6期)2015-06-17
中学数学杂志(初中版)(2014年1期)2014-02-28
数学教学(2013年8期)2013-11-18
福建中学数学(2011年9期)2011-11-03
中学生数理化·高二版(2008年10期)2008-06-17
中学生数理化·高一版(2008年11期)2008-06-15

